Théorème de Harnack
En géométrie algébrique réelle, le théorème de Harnack donne les nombres possibles de composantes connexes que peut avoir une courbe algébrique réelle, en fonction du degré (ou du genre) de la courbe. Pour une courbe algébrique de degré m du plan projectif réel, le nombre c de composantes est borné par:
De plus, pour tout nombre vérifiant ces inégalités, il existe des courbes qui ont exactement ce nombre de composantes.
Ce théorème est à la base du seizième problème de Hilbert.
Le nombre maximum () vaut 1 de plus que le genre d'une courbe non-singulière de degré m.
Une courbe qui atteint le nombre maximum possible de composantes réelles pour son degré est appelée une M-courbe (M pour "maximum") – par exemple, une courbe elliptique à deux composantes connexes ou la courbe de Trott, une courbe quartique avec quatre composantes connexes, sont des exemples de M-courbes.
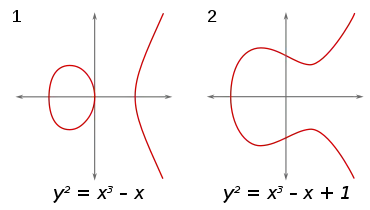La courbe elliptique (lisse de degré 3) sur la gauche est une M-courbe, car elle a le nombre maximum (2) de composantes connexes, tandis que la courbe elliptique à droite n'a qu'une seule composante.
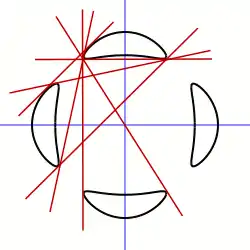La courbe de Trott, montrée ici avec 7 de ses bitangentes, est une M-courbe quartique (i.e. de degré 4), car elle atteint le maximum (4) de composantes connexe d'une courbe de ce degré.
Références
- C. G. A. Harnack, Ueber die Vieltheiligkeit der ebenen algebraischen Curven, Math. Ann. 10 (1876), 189-199.
- G. Wilson, Hilbert's sixteenth problem, Topology 17 (1978), 53-74
- J. Bochnak, M. Coste, M.-F. Roy, Real Algebraic Geometry. Series: Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern. Surveys in Mathematics, Vol. 36, Springer, 1998.
- R. Benedetti, J.-J. Risler, Real algebraic and semi-algebraic sets. Actualités mathématiques, Hermann, 1990.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Harnack's curve theorem » (voir la liste des auteurs).