On va tout d'abord montrer que  .
.
Comme  est symétrique on a :
est symétrique on a :

En particulier  représente le nombre de 1 dans la i-ème ligne de
représente le nombre de 1 dans la i-ème ligne de  . Ainsi en remplaçant dans l'équation on obtient :
. Ainsi en remplaçant dans l'équation on obtient :
 et donc
et donc  .
.
D'autre part on a aussi  . Ainsi en remplaçant à nouveau dans l'équation on obtient :
. Ainsi en remplaçant à nouveau dans l'équation on obtient :
 et donc
et donc 
.
Cherchons ensuite des contraintes sur les valeurs propres de la matrice  .
.
Soit donc  une valeur propre de
une valeur propre de  et
et  un vecteur propre associé. On a donc aussi :
un vecteur propre associé. On a donc aussi :

Et donc  est une valeur propre de la matrice
est une valeur propre de la matrice  associée à
associée à  , or cette matrice a pour valeurs propres 0 (associée à un sous-espace propre de dimension
, or cette matrice a pour valeurs propres 0 (associée à un sous-espace propre de dimension  ) et
) et  (associé à un sous-espace propre de dimension
(associé à un sous-espace propre de dimension  ) avec de plus
) avec de plus  .
.
Ainsi :
- soit
 et alors
et alors  ;
;
- soit
 et donc
et donc  avec :
avec : .
.
Donnons les valeurs possible pour d.
 donc elle est diagonalisable avec comme valeurs propres
donc elle est diagonalisable avec comme valeurs propres  et des sous-espaces propres associés de dimensions
et des sous-espaces propres associés de dimensions  , et comme la trace de
, et comme la trace de  est nulle on a :
est nulle on a :

La seconde équation donne :
 donc d'après la première relation
donc d'après la première relation  ou encore
ou encore  .
.
- Si
 alors
alors  .
.
- Sinon, on doit avoir
 donc
donc  on a alors
on a alors  donc
donc  divise
divise  donc
donc  divise
divise  donc en particulier
donc en particulier  divise 15 et donc
divise 15 et donc  d'où
d'où  .
.
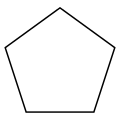 Le pentagone est un graphe de Moore à 5 sommets ().
Le pentagone est un graphe de Moore à 5 sommets ().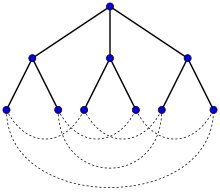 Le graphe de Petersen est un graphe de Moore à 10 sommets ().
Le graphe de Petersen est un graphe de Moore à 10 sommets ().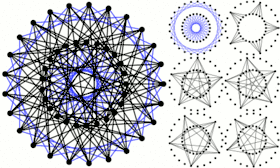 Le graphe de Hoffman-Singleton est un graphe de Moore à 50 sommets ().
Le graphe de Hoffman-Singleton est un graphe de Moore à 50 sommets ().













































