Taux d'amortissement (physique)

Différents régimes de retour à l'équilibre en fonction de la valeur du taux d'amortissement ζ. Les régimes apériodique (ζ>1), critique (ζ=1), pseudo-périodique (ζ<1) et harmonique (ζ=0). La courbe représente les oscillations (x(t)) relatives à la position de départ (x(0)) d'un oscillateur mécanique à une dimension sans vitesse initiale. ω₀ est la pulsation propre du système.

Pour un oscillateur harmonique amorti, constitué d'une masse m, amorti par frottement fluide de coefficient c et soumis à une force de rappel élastique de constante de raideur k, l'équation différentielle modélisant le comportement de l'oscillateur est :

${\displaystyle m{\frac {{\textrm {d}}^{2}x}{{\textrm {d}}t^{2}}}+c{\frac {{\textrm {d}}x}{{\textrm {d}}t}}+kx=0}$.

Il est possible de réécrire cette équation sous la forme canonique :

${\displaystyle {\frac {{\textrm {d}}^{2}x}{{\textrm {d}}t^{2}}}+2\zeta \omega _{0}{\frac {{\textrm {d}}x}{{\textrm {d}}t}}+\omega _{0}^{2}x=0}$,

où ${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$ est la pulsation propre de l'oscillateur harmonique et ${\displaystyle \zeta ={\frac {c}{2{\sqrt {km}}}}}$ est le taux d'amortissement.

On résout le polynôme caractéristique associé :

${\displaystyle \omega ^{2}+2\zeta \omega _{0}\omega +\omega _{0}^{2}=0}$.

D'où ${\displaystyle \omega =\omega _{0}\left(-\zeta \pm {\sqrt {\zeta ^{2}-1}}\right)}$.

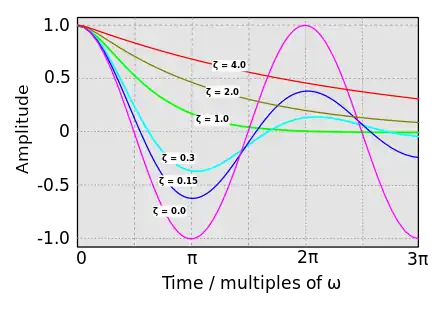
Différents régimes

Périodique

si ω est purement imaginaire, la solution est une sinusoïde de la forme ${\displaystyle e^{\pm j\omega _{0}t}}$. Ceci correspond au cas d'un oscillateur harmonique. Il apparaît pour le cas limite ${\displaystyle \zeta =0}$.

Pseudo-périodique

si ω est complexe, la solution est le produit d'une exponentielle décroissante et d'une sinusoïde de la forme ${\displaystyle e^{\omega _{0}(-\zeta \pm j{\sqrt {1-\zeta ^{2}}})t}}$. Ce phénomène apparaît pour ${\displaystyle \zeta <1}$.

Apériodique critique

c'est la frontière entre le régime pseudo-périodique et le régime apériodique. C'est souvent la solution optimale à un problème d'oscillations amorties. Il apparaît pour le cas limite ${\displaystyle \zeta =1}$.

Apériodique

si ω est réelle, la solution est simplement une exponentielle décroissante sans oscillation. Il apparaît pour le cas ${\displaystyle \zeta >1}$.

La forme canonique de l'équation différentielle du paragraphe précédent peut se reformuler comme suit ... :

${\displaystyle {\frac {d^{2}x}{dt^{2}}}=-\left(2\zeta \omega _{0}{\frac {dx}{dt}}+\omega _{0}^{2}x\right)}$

Ce qui permet d'en déduire un schéma-bloc basé sur les opérateurs élémentaires que sont l'intégrateur, le sommateur et le gain (à gauche ci-dessous).

Dans le cas particulier où le coefficient d'amortissement est nul, le schéma se simplifie en deux intégrateurs interconnectés en anneau (la sortie de l'un est connectée à l'entrée de l'autre), avec un gain de boucle égal au carré de la pulsation propre (au centre ci-dessous).

Cette topologie est exploitée dans la conception d'oscillateurs électroniques analogiques (à droite ci-dessous) ou numériques.

• Différents types d'oscillateurs
• 
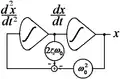  Oscillateur amorti à variables d'état
• 
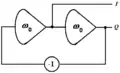  Oscillateur en quadrature (In phase, in Quadrature)
• 
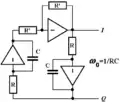  Réalisation électronique d'un oscillateur en quadrature

Exemple de produit commercial : le filtre actif universel UAF42[1].

Le facteur de qualité de l'oscillateur linéaire harmonique amorti à un degré de liberté décrit ci-dessus étant défini par :

${\displaystyle Q={\frac {\sqrt {k\,m}}{c}}}$

on en déduit immédiatement une relation liant le taux d'amortissement au facteur de qualité :

${\displaystyle Q={\frac {1}{2\,\zeta }}}$.

• Amortissement physique
• Décrément logarithmique (une méthode pour déterminer le taux d'amortissement)
• Méthode d'Oberst (autre méthode)
• Analyse mécanique dynamique (autre méthode)
• Facteur de qualité
• Oscillations amorties