Tangente hyperbolique réciproque

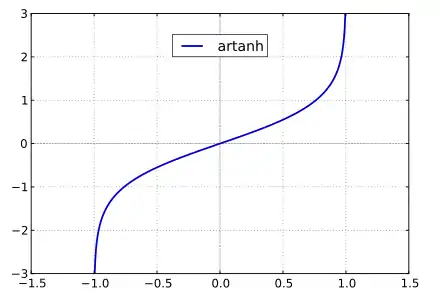
La fonction tangente hyperbolique réciproque, ou argument tangente hyperbolique[1], notée artanh[2] (ou argth), ${\displaystyle \operatorname {artanh}$ :\left]-1,+1\right[\to \mathbb {R} } est définie à l'aide de la tangente hyperbolique par : ${\displaystyle y=\operatorname {artanh} x\quad \Longleftrightarrow \quad x=\tanh y\ \mathrm {et} \ |y|<1}$.

Cette fonction est bijective, impaire et son image est ${\displaystyle \mathbb {R} }$. Elle est continue, strictement croissante, concave sur ${\displaystyle \left]-1,0\right[}$ et convexe sur ${\displaystyle \left]0,+1\right[}$.

Sa valeur en 0 est 0 et sa limite en 1 est +∞.

Elle est dérivable sur ${\displaystyle \left]-1,1\right[}$ et sa dérivée est donnée par ${\displaystyle \forall |x|<1\quad \operatorname {artanh} 'x={\frac {1}{1-x^{2}}}}$.

Par conséquent[3], la fonction artanh s'exprime à l'aide du logarithme naturel par[4] ${\displaystyle \forall |x|<1\quad \operatorname {artanh} x={\frac {1}{2}}\ln \left({\frac {1+x}{1-x}}\right)}$.

(en) Eric W. Weisstein, « Inverse Hyperbolic Tangent », sur MathWorld