Surface de Bézier
Les surfaces de Bézier sont une méthode de définition d'une surface grâce aux courbes de Bézier, avantageuses pour définir une courbe par la donnée de points de contrôle. Elles servent à construire une surface lisse à partir de points de contrôle, et leur simplicité de définition en font un outil important de la visualisation graphique.
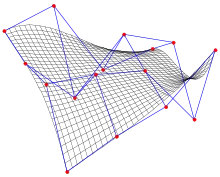
Historique
L'ingénieur Pierre Bézier a posé le principe de ces surfaces en 1962 pour concevoir des structures d'automobile. Par expérience, si les surfaces de Bézier peuvent être de degré quelconque, les surfaces bicubiques présentent suffisamment de degrés de liberté pour avoir une haute précision.
Définition
Étant donné une matrice [M] de (n + 1)(m + 1) points de l'espace {Ai,j }i∈{0,n}, j∈{0,m} , la surface de Bézier correspondante est l'ensemble des points M généré par les valeurs comprises entre 0 et 1 des variables u et v du polynôme :
avec Bn les polynômes de Bernstein.
Propriétés
Les points ainsi définis sont évidemment indépendants du choix du point O.
Les surfaces de Bézier ont des propriétés similaires aux courbes de Bézier dans un espace de dimension 3 :
- la forme de la surface
- l'ensemble de la surface est dans l'enveloppe convexe de l'ensemble des points de contrôle.
Les cas particuliers n = 1 (ou m = 1) correspond aux surfaces réglées. Si m = n = 1, on obtient une surface deux fois réglée, qui est soit un plan si les quatre points sont coplanaires, soit un paraboloïde hyperbolique. En considérant sur une telle surface les intersections de deux paires de règles voisines, on se rend compte que la donnée de quatre points ne fait pas que définir la nature de la surface, mais sert aussi à en arrêter les frontières. Dans le cas général, les courbes de Bézier correspondant aux sous-ensembles de points A0,j, An,j, Ai,0 et Ai,m définissent les frontières de la surface.
Liens internes
Référence
Pierre Bézier, Courbes et Surfaces, Hermes, 1996
