Suite de Padovan

La suite de Padovan est la suite d'entiers $(P n)$ définie par récurrence par[1] :

P_{0}=P_{1}=P_{2}=1{\text{ et }}\forall n\in \mathbb {N} \quad P_{n+3}=P_{n+1}+P_{n}.

Construction de la suite de Padovan à l'aide de triangles équilatéraux.

C'est une suite récurrente linéaire qui ressemble dans sa forme à la suite de Fibonacci, à une nuance près : la somme des termes de rang $n$ et $n$ + 1 ne donne pas le terme de rang $n$ + 2 mais celui de rang $n$ + 3.

La suite porte le nom de l'architecte Richard Padovan (en) et est associée au nombre plastique étudié par l'architecte puis moine Hans van der Laan[2]. Le mathématicien Ian Stewart, dans ses Mathematical Recreations, évoque et étudie cette suite et lui attribue le nom de suite de Padovan[3].

Le terme général de la suite de Padovan est lié aux trois racines du polynôme X³ – X – 1.

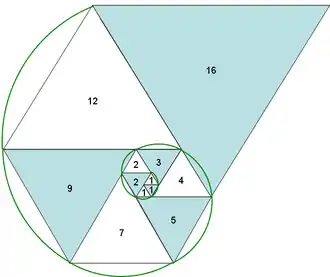
Le quotient de deux termes consécutifs tend vers le nombre plastique.

Termes et propriétés

La série génératrice est :

F(X)={\frac {1+X}{1-X^{2}-X^{3}}}.

Cette suite d'entiers est strictement croissante à partir du rang 3 ; ses termes sont :

1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, etc. (suite A134816 de l'OEIS).

Ils s'expriment en fonction des trois racines $r 1$ , $r 2$ et $r 3$ de X³ – X – 1 (une réelle et deux complexes conjuguées) :

P_{n}={\frac {(1-r_{2})(1-r_{3})}{(r_{1}-r_{2})(r_{1}-r_{3})}}r_{1}^{n}+{\frac {(1-r_{3})(1-r_{1})}{(r_{2}-r_{3})(r_{2}-r_{1})}}r_{2}^{n}+{\frac {(1-r_{1})(1-r_{2})}{(r_{3}-r_{1})(r_{3}-r_{2})}}r_{3}^{n}.

Les formules de Cardan donnent pour la racine réelle le nombre plastique :

{\sqrt[{3}]{{\frac {1}{2}}+{\frac {\sqrt {69}}{18}}}}+{\sqrt[{3}]{{\frac {1}{2}}-{\frac {\sqrt {69}}{18}}}}\approx 1,32472.

Les nombres de Padovan premiers sont 2, 3, 5, 7, 37, 151, etc.(suite A100891 de l'OEIS).

Variantes

On trouve parfois des initialisations différentes comme dans les suites A000931, A078027, A096231, A124745, A133034, A164001, A182097, A228361, A020720 et A001608 de l'OEIS.

Cette dernière est la suite de Perrin : 3, 0, 2, 3, 2, 5, etc.

Notes et références

(en) Eric W. Weisstein, « Padovan sequence », sur MathWorld.
(en) Richard Padovan presents the plastic number, résumé du Nexus Network Journal
(en) Tales of a Neglected Number, dans Mathematicla Recreations de Ian Stewart

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.