Stencil (analyse numérique)

En mathématiques, un stencil est une représentation géométrique d'un réseau nodal illustrant les points d'intérêt utilisés dans un schéma de discrétisation pour la résolution numérique des équations différentielles, notamment des équations aux dérivées partielles combinant variables temporelles et spatiales.

Le stencil de la méthode de Crank-Nicolson en une dimension.

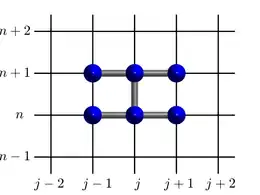
Les stencils peuvent être compacts ou non, selon les niveaux utilisés autour du point d'intérêt.

Étymologie

Les représentations graphiques d'arrangements nodaux et les coefficients associés sont vite apparus dans l’étude des équations aux dérivées partielles. Certains auteurs utilisent des termes différents, comme "schémas de relaxation", "instructions opérantes", "logenzes", ou "schémas de points"[1] - [2]. Le mot "stencil" a été retenu pour de tels schémas pour refléter l'utilisation d'un stencil sur une grille de calcul afin de repérer uniquement les points utiles[2].

Calcul de coefficients

Les coefficients de différences finies pour un stencil donné dépendent du choix des points. Ils peuvent s'obtenir par le calcul des dérivées des polynômes de Lagrange interpolant ces points[3], par résolution d'un système linéaire obtenu à partir d'un développement de Taylor autour de chaque point[4] ou en imposant que le stencil est exact pour chaque monôme jusqu'au degré du schéma[3]. Dans le cas des points équirépartis, on peut également utiliser efficacement l'approximant de Padé de $x s (log x) m$ , avec $m$ l'ordre de dérivation recherché et $s$ la « distance » entre les nœuds de calcul les plus à gauche sur les deux étages du stencil[5].

Avec les polynômes interpolateurs de Lagrange

Un moyen d'obtenir les poids des différences finies est de passer par la dérivation du polynôme interpolateur de Lagrange aux nœuds de calcul du stencil choisi. Pour un stencil de longueur n, on note les polynômes d'interpolation :

\ell _{j}(\xi )=\prod _{i=0,\,i\neq j}^{n}{\frac {\xi -x_{i}}{x_{j}-x_{i}}},

On obtient ainsi un polynôme $p n (x)$ de degré n interpolant $ƒ (x)$ en ces n points

p_{n}(x)=\sum _{j=0}^{n}f(x_{j})\ell _{j}(x)

et de son polynôme dérivé

p_{n}'(x)=\sum _{j=0}^{n}f(x_{j})\ell '_{j}(x).

Ainsi, on a l'approximation de la dérivée première au point $x c$ avec :

f'(x_{c})=\sum _{j=0}^{n}f(x_{j})\ell '_{j}(x_{c})+O(h^{n}).

Le calcul des coefficients $(\ell _{j}'(x_{c}))$ permet de retrouver les coefficients obtenus auparavant.

On remarque que la formule est totalement définie sans un pas de discrétisation, ce qui la rend directement applicable aux grilles non uniformes.

Avec les approximants de Padé

Les coefficients de pondération des schémas peuvent être également déterminés par un approximant de Padé, dans le cas où le schéma est semi-implicite.

On considère un stencil de la forme :

\sum _{k=0}^{m}b_{k}f^{(d)}(x_{k})\approx \sum _{j=-s}^{n}c_{j}f(x_{j})

où les points $x i$ sont sur une grille régulière de pas $h$ , soit donc $x i = x + ih$ . On remplace $f (x) = e iω x$ :

\sum _{k=0}^{m}b_{k}(\mathrm {i} \omega )^{d}\mathrm {e} ^{\mathrm {i} \omega x_{k}}=\sum _{j=-s}^{n}c_{j}\mathrm {e} ^{\mathrm {i} \omega x_{j}}\ \Longleftrightarrow \ \mathrm {e} ^{\mathrm {i} \omega x}(\mathrm {i} \omega )^{d}\sum _{k=0}^{m}b_{k}\mathrm {e} ^{\mathrm {i} \omega kh}=\mathrm {e} ^{\mathrm {i} \omega x}\sum _{j=-s}^{n}c_{j}\mathrm {e} ^{\mathrm {i} \omega jh}=\mathrm {e} ^{\mathrm {i} \omega x}\mathrm {e} ^{-\mathrm {i} \omega sh}\sum _{j=0}^{n+s}c_{j-s}\mathrm {e} ^{\mathrm {i} \omega jh}

On pose $ξ = e iω h$ . Le schéma se réécrit alors, par abus de notation :

\xi ^{s}\left({\frac {\ln \xi }{h}}\right)^{d}={\frac {\sum _{j=0}^{n}c_{j}\xi ^{j}}{\sum _{k=0}^{m}b_{k}\xi ^{k}}}.

Les coefficients optimaux s'obtiennent donc en calculant l'approximant de Padé d'ordre $[n, m]$ autour de $ξ = 1$ .

Compacité du stencil

Un stencil compact 2D utilisant le nœud central (en rouge) et les 8 nœuds adjacents.

Un stencil compact n'utilise que neuf points pour la discrétisation en 2D, en l'occurrence le nœud central et les nœuds adjacents. Ainsi, sur une grille structurée utilisant un stencil compact en dimension 1, 2 ou 3, le nombre maximum de nœuds utilisés est de 3, 9 ou 27 respectivement.

Les stencils compacts sont couramment utilisés et sont au cœur de plusieurs solveurs basant leurs modèles sur des équations aux dérivées partielles[6] - [7]

Un stencil non compact 2D.

À l'inverse, un stencil non compact peut faire intervenir tout nœud du voisinage du nœud d'intérêt. Le principal désavantage est que l’utilisation de points éloignés va augmenter le temps de calcul nécessaire à la résolution.

Stencils en une dimension

À deux points

Le stencil à deux points pour la dérivée première d'une fonction est donné par :

f'(x_{0})={\frac {f\left(x_{0}+h\right)-f\left(x_{0}-h\right)}{2h}}+O\left(h^{2}\right)

qui est obtenu classiquement par un développement limité autour de $x 0$ :

{\begin{aligned}f'(x_{0})&={\frac {f\left(x_{0}+h\right)-f(x_{0})}{h}}-{\frac {f^{(2)}(x_{0})}{2!}}h-{\frac {f^{(3)}(x_{0})}{3!}}h^{2}-{\frac {f^{(4)}(x_{0})}{4!}}h^{3}+\cdots \\f'(x_{0})&=-{\frac {f\left(x_{0}-h\right)-f(x_{0})}{h}}+{\frac {f^{(2)}(x_{0})}{2!}}h-{\frac {f^{(3)}(x_{0})}{3!}}h^{2}+{\frac {f^{(4)}(x_{0})}{4!}}h^{3}+\cdots \end{aligned}}

À trois points

Le stencil à trois points pour la dérivée seconde d'une fonction est donné par :

f''(x_{0})={\frac {f\left(x_{0}+h\right)-2f(x_{0})+f\left(x_{0}-h\right)}{h^{2}}}+O(h^{2}).

Ce stencil compact est le plus usuel pour cette dérivée.

À cinq points

Le stencil à 5 points en une dimension s'étend sur la grille

\ \{x_{0}-2h,x_{0}-h,x_{0},x_{0}+h,x_{0}+2h\}.

Le stencil pour la dérivée première est donné par :

f'(x_{0})\approx {\frac {-f(x_{0}+2h)+8f(x_{0}+h)-8f(x_{0}-h)+f(x_{0}-2h)}{12h}}

Il est obtenu à partir des développements limités autour de $x 0$ de $ƒ (x 0 \pm h)$ et $ƒ (x \pm 2 h)$ jusqu'à l'ordre 3 (5 si on cherche également une estimation de l'erreur) et en recombinant les quatre équations obtenues. On remarque ainsi qu'on a :

{\begin{aligned}f(x+h)-f(x-h)&=2hf'(x)+{\frac {h^{3}}{3}}f^{(3)}(x)+O(h^{4})\\f(x+2h)-f(x-2h)&=4hf'(x)+{\frac {8h^{3}}{3}}f^{(3)}(x)+O(h^{4})\end{aligned}}

dont on tire :

8(f(x+h)-f(x-h))-(f(x+2h)-f(x-2h))=12hf'(x)+O(h^{4})\,

Formellement, on devrait avoir des O(h⁵) mais on peut l'écrire ainsi sans perte de généralités dans ce cadre.

Le jeu de coefficients (8, -8,-1,1) obtenu ici est un cas spécifique de l'algorithme de Savitzky-Golay.

Estimation de l'erreur

En utilisant les termes d'ordre supérieur (négligés pour l'obtention du stencil), on a une estimation de l'erreur de ce schéma [8] :

{\frac {-f(x+2h)+8f(x+h)-8f(x-h)+f(x-2h)}{12h}}=f'(x)-{\frac {1}{30}}f^{(5)}(x)h^{4}+O(h^{5}).

Dérivées d'ordres supérieurs

Sur un schéma à cinq points, on peut obtenir des formules centrées (avec une symétrie dans les coefficients autour du nœud central) pour les dérivées d'ordres supérieurs[8] :

{\begin{aligned}f''(x)&\approx {\frac {-f(x+2h)+16f(x+h)-30f(x)+16f(x-h)-f(x-2h)}{12h^{2}}}+O(h^{4})\\f^{(3)}(x)&\approx {\frac {f(x+2h)-2f(x+h)+2f(x-h)-f(x-2h)}{2h^{3}}}+O(h^{2})\\f^{(4)}(x)&\approx {\frac {f(x+2h)-4f(x+h)+6f(x)-4f(x-h)+f(x-2h)}{h^{4}}}+O(h^{2})\end{aligned}}

Deux dimensions

Sur une grille régulière 2D, le stencil à 5 points autour du nœud (x, y) est donc donné par :

\{(x-h,y),(x,y),(x+h,y),(x,y-h),(x,y+h)\},\,

Il forme donc un quinconce.

Il apparait dans le calcul du laplacien discret d'une fonction à deux variables[9]:

\Delta f(x,y)\approx {\frac {f(x-h,y)+f(x+h,y)+f(x,y-h)+f(x,y+h)-4f(x,y)}{h^{2}}}+O(h^{2}).

Stencils des schémas numériques usuelles

Les stencils sont représentés graphiquement sur une grille : le nœud $(j, n)$ correspond au point $u (x j, t n)$ utilisé dans le schéma.

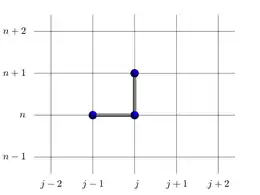Schéma d'Euler 1D (décentrage aval)
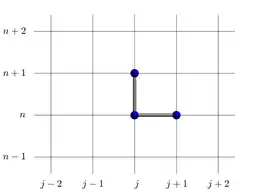Schéma d'Euler 1D (décentrage amont)
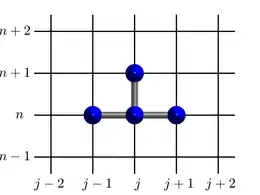Schéma d'Euler 1D (centré)
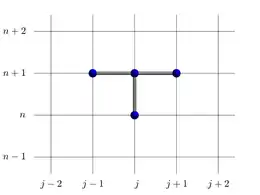Schéma d'Euler implicite 1D
Schéma de Crank-Nicholson 1D

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Stencil (numerical analysis) » (voir la liste des auteurs).
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Compact_stencil » (voir la liste des auteurs).
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Five-point_stencil » (voir la liste des auteurs).

Howard W. Emmons, « The numerical solution of partial differential equations », Quarterly of Applied Mathematics, vol. 2, n^o 3,‎ 1^er octobre 1944, p. 173–195 (DOI 10.1090/qam/10680, lire en ligne, consulté le 17 avril 2017)
(en) William Edmund Milne, Numerical solution of differential equations., Wiley, 1953, 1^re éd., 128–131 p. (lire en ligne)
Bengt Fornberg et Natasha Flyer, A Primer on Radial Basis Functions with Applications to the Geosciences, Society for Industrial and Applied Mathematics, 2015, 221 p. (ISBN 978-1-61197-402-7, DOI 10.1137/1.9781611974041.ch1, lire en ligne), « Brief Summary of Finite Difference Methods »
(en) Cameron Taylor, « Finite Difference Coefficients Calculator », sur web.media.mit.edu (consulté le 9 avril 2017)
Bengt Fornberg, « Classroom Note: Calculation of Weights in Finite Difference Formulas », SIAM Review, vol. 40, n^o 3,‎ janvier 1998, p. 685–691 (DOI 10.1137/S0036144596322507)
W. F. Spotz. High-Order Compact Finite Difference Schemes for Computational Mechanics. PhD thesis, University of Texas at Austin, Austin, TX, 1995.
Abramowitz & Stegun, Table 25.2
Abramowitz & Stegun, 25.3.30

(en) W. F. Spotz., High-Order Compact Finite Difference Schemes for Computational Mechanics. PhD thesis, Austin, University of Texas at Austin, 1995 (lire en ligne).
(en) Milton Abramowitz et Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables [détail de l’édition] (lire en ligne). Ninth printing. Table 25.2.

Voir aussi

Dérivation numérique

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.