Site cristallographique

Un site cristallographique, ou site cristallin, est une position particulière dans un réseau cristallin. Les positions normalement occupées par les atomes du cristal sont appelées « sites réguliers » ou « sites du réseau » ; les centres des espaces restant entre ceux-ci, normalement inoccupés, sont appelés « sites interstitiels ».

Exemple du réseau cubique à faces centrées

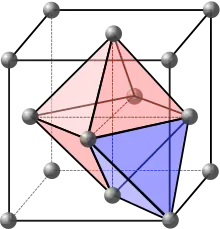
Maille conventionnelle d'un réseau cubique à faces centrées. Les atomes du réseau, représentés ici par de petites boules sphériques (en gris) pour une meilleure lisibilité, sont en réalité des sphères jointives, leur rayon étant égal au quart de la diagonale des faces carrées.

La maille primitive d'un réseau cubique à faces centrées ayant des axes obliques, il est plus commode d'en étudier la maille conventionnelle (figure ci-contre).

Les sites réguliers sont les positions des atomes. Si l'on désigne par $a$ le côté des faces carrées, ces positions sont $(0,0,0)$ , $(0,{\tfrac {a}{2}},{\tfrac {a}{2}})$ , $({\tfrac {a}{2}},0,{\tfrac {a}{2}})$ , $({\tfrac {a}{2}},{\tfrac {a}{2}},0)$ et toutes celles qui s'en déduisent par les translations du réseau cubique, $(+n_{x}a,+n_{y}a,+n_{z}a)$ où $n_{x}$ , $n_{y}$ et $n_{z}$ sont des entiers algébriques. Il y en a 4 par maille conventionnelle (les atomes aux 8 sommets comptent pour $1 / 8$ chacun et les atomes au centre des 6 faces pour $1 / 2$ chacun).

Les sites interstitiels sont au centre des espaces des groupes de 6 atomes jointifs 3 par 3 (sites octaédriques, en rose sur la figure) et au centre des groupes de 4 atomes jointifs (sites tétraédriques, en violet sur la figure) :

dans la maille conventionnelle on trouve les sites octaédriques au centre du cube et au centre des 12 arêtes, il y en a donc 4 par maille (le site au centre du cube compte pour 1, et chacun des sites au centre d'une arête pour $1 / 4$ ) ;
on montre de même qu'il y a 8 sites tétraédriques par maille conventionnelle.

Les sites tétraédriques sont plus exigus que les sites octaédriques.

Dans l'autre réseau compact régulier, le réseau hexagonal compact, il y a également autant de sites octaédriques que de sites réguliers et deux fois plus de sites tétraédriques ; leurs tailles sont les mêmes que dans le réseau cubique à faces centrées mais leurs dispositions relatives sont différentes.

Taille des sites

La taille d'un site cristallographique est le rayon maximal d'une sphère pouvant se loger dans le site. Dans un empilement compact[1] :

la taille d'un site régulier est le rayon de l'atome qui l'occupe normalement. Dans le cas d'un réseau cubique à faces centrées dont le paramètre de maille (la longueur d'un côté du cube) est $a$ , cette taille est $r=a/{\sqrt {2}}\approx$ 0,707 $a$ ;
la taille des sites octaédriques est $r_{\mathrm {O} }=({\sqrt {2}}-1)\,r\approx$ 0,414 $r$ ;
la taille des sites tétraédriques est $r_{\mathrm {T} }=\left({\sqrt {\tfrac {3}{2}}}-1\right)r\approx$ 0,225 $r$ .

Réseau de référence

En pratique on peut définir les sites réguliers et les sites interstitiels :

par rapport au système réticulaire du composé cristallin considéré ;
ou par rapport à un sous-réseau ne comportant qu'une partie des atomes du composé.

Dans le premier cas, tous les sites réguliers du cristal idéal sont occupés et tous les sites interstitiels sont inoccupés. Un cristal réel, en revanche, comporte des défauts cristallins plus ou moins nombreux, et notamment des sites réguliers inoccupés (lacunes) et des sites interstitiels occupés (atomes interstitiels). Ces défauts sont en général distribués aléatoirement au sein de la structure.

Dans le second cas, une partie des sites interstitiels du cristal idéal sont occupés (par les atomes non pris en compte dans le sous-réseau) et il peut arriver qu'une partie des sites réguliers soient inoccupés (avec la périodicité du système réticulaire). Un cristal réel comporte en plus des défauts, dont les lacunes et les atomes interstitiels.

Exemple des nésosilicates

Les nésosilicates sont constitués d'un empilement quasi compact d'anions oxygène O²⁻ entre lesquels sont disposés régulièrement des cations métalliques de plus petite taille comme Mg²⁺ et Fe²⁺ et des cations silicium Si⁴⁺ encore plus petits. Pour comprendre l'organisation des atomes dans l'espace, il est donc intéressant de prendre comme réseau de référence le sous-réseau des anions oxygène. Dans la forstérite Mg₂SiO₄, par exemple, les anions occupent les sites réguliers d'un réseau hexagonal quasi compact, les cations Mg²⁺ occupent un site octaédrique sur deux, et les cations Si⁴⁺ un site tétraédrique sur huit (la disposition des sites occupés est régulière)[2].

Notes et références

(en) « Study of interstitial voids », sur Chemzipper, 20 avril 2019 (consulté le 16 décembre 2022).
(en) « Olivine », sur Université de Cambridge (consulté le 17 décembre 2022).

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.