Simulation atomistique
La simulation atomistique est l'ensemble des méthodes de simulation utilisant une description atomistique pour simuler la matière solide, liquide ou encore moléculaire. Elle consiste en une alternative à la modélisation macroscopique. En se basant sur les mécanismes élémentaires à l'échelle atomique, elle permet d'accéder aux données quantitatives fournies par les modèles macroscopiques.
Ces méthodes sont de puissants outils qui soutiennent la recherche sur les matériaux dans le développement d’applications nouvelles ou améliorées. Elles fournissent les informations essentielles pour identifier les nouveaux matériaux, adapter les matériaux et concevoir les matériaux pour les structures et les systèmes. L’utilisation de la modélisation des matériaux dans les industries est très polyvalente. Les applications couvrent des domaines tels que l’énergie, l’environnement, les transports, la santé, et la fabrication. Il soutient la création de produits comme les cellules solaires, les capteurs, les pièces automobiles, les tissus, les ordinateurs, l’outillage, les revêtements etc. En général, la modélisation et les simulations peuvent être les yeux des expérimentateurs, les aidant à accéder à des informations qui ne seraient pas disponibles autrement et à interpréter les résultats expérimentaux. La modélisation fournit également des prédictions inestimables sur l’évolution d’un système d’une manière plus rapide ou moins coûteuse qu’avec des méthodes d’essai et d’erreur[1].
Au cours des dernières décennies, un développement important des outils de calculs a été observé. L'utilisation de la simulation atomistique date des années 1950 et l’intérêt de ces techniques ne cesse de croître dans le domaine des matériaux. Nous pouvons noter des avancées récentes en théorie de la matière condensée (supraconducteurs, magnétorésistance) et des projets de techniques de caractérisation à l'échelle atomique.
L'échelle atomique est difficilement accessible expérimentalement. C'est pour cela que la simulation atomistique présente deux enjeux principaux. Elle permet de modéliser les propriétés électroniques et mécaniques des matériaux à l'échelle atomique, dans le but d'affiner la compréhension physique et d'anticiper et repousser les limites des technologies émergentes. Elle consiste également à simuler les nano-objets pour comprendre et optimiser leurs propriétés structurales, optiques et de transports [2].
Histoire
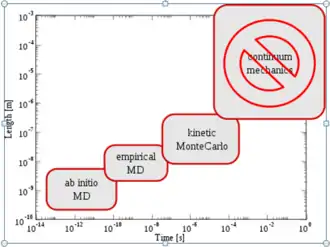
À la suite du modèle de l’atome établit par Niels Bohr, en 1925, Erwin Schrödinger, s’intéressant à la mécanique quantique affirme que les électrons sont introuvables et qu’on ne peut formuler qu’une probabilité quant à leur position. Il vient toujours un moment ou les expériences réelles deviennent trop limitées, voire impossible. Il faut donc contourner le problème, oublier les expériences et faire des simulations. Moins précises, moins fiables, mais aussi moins limitées. Tout commence avec Nicholas Constantine Metropolis. Il dirige en 1952 un projet de construction d’un ordinateur de calcul : le MANIAC analyseur mathématique, intégrateur numérique et ordinateur.
Par la suite, les simulations informatiques se firent de plus en plus nombreuses : la physique arrivait dans une période où les expériences physiques étaient trop poussées pour être réalisées. Les ordinateurs se développant de plus en plus rapidement, et leur utilisation devenant grand public, la simulation devint même courante et peu chère.
En 1953, Metropolis met en place avec Ulam la méthode de Monte-Carlo, tirant son nom des jeux de hasard pullulant dans casino Monte-Carlo, qui désigne une famille de méthodes algorithmiques visant à calculer une valeur numérique approchée en utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes.
En 1957, ce sont Alder et Wainright qui effectuent alors des simulations par ordinateur avec un concept original : ils appliquent les lois de Newton à chaque atome, cela donnant naissance à la dynamique moléculaire.
En 1985, l'explosion de la puissance des ordinateurs permet à Car et Parinello de calculer la dynamique de particules grâce à la dynamique moléculaire quantique.
Les simulations sont très utilisées dans le secteur des matériaux, elles permettent de prévoir leurs déformations, leur résistance et leurs déchirures sous certaines contraintes.
Aujourd'hui, le développement récent des méthodes atomistiques et la puissance des machines de calcul permettent de simuler avec une très grande précision les propriétés électroniques et optiques de systèmes comprenant jusqu'à plusieurs millions d'atomes. Aussi bien les petits détails de la structure de bande que ses aspects globaux sont reproduits de façon quantitative [3].
Les grandes familles de description énergétique des interactions au sein du solide
Méthodes ab initio
Les méthodes Premiers Principes permettent d'accéder de manière rigoureuse à la structure électronique qui régit une grande partie des interactions entre atomes [4]. Ces méthodes sont basées sur la théorie de la fonctionnelle de la densité, elle-même basée sur plusieurs approximations.
Approximation de Born-Oppenheimer
Cette approche est aujourd’hui à la base de beaucoup de calculs en physique de la matière . Partant du simple constat que les électrons sont beaucoup moins lourds que les noyaux, on peut affirmer que leur mouvement est bien plus rapide. L'équation de Schrödinger est résolue en deux étapes : tout d’abord, on résout l’équation électronique en posant les noyaux fixes puis on résout l’équation dans le potentiel créé par les électrons. En conséquence, il est possible de considérer que les déplacements de l’électron se font autour d’un repère fixe : le noyau atomique. L’approximation de Born-Oppenheimer n’est valable que lorsque les couplages des mouvements électroniques sont négligeables, c’est-à-dire quand la fonction d’onde ne subit pas de variations brusques lorsque les noyaux varient. Evidemment, cette théorie est invalidée dans des cas d’une collision entre atomes, la vitesse des noyaux devenant un paramètre essentiel[5].
Approximation Hartree-Fock
Cette approximation est très importante car elle est à la base de presque toutes les méthodes ab initio (basées sur la fonction d'onde). Il n'existe de solutions exactes que pour des systèmes simples tel que l'atome d'hydrogène dû à la complexité des systèmes qui couplent le mouvement des électrons entre eux. L’approximation de Hartree-Fock part du principe que seul l’effet moyen de la répulsion électron-électron est pris en compte, entre d’autres termes, les effets causés par la présence d’autres électrons autour de celui étudié sont quasiment ignorés pour la plupart. La répulsion électron-électron se voit donc incluse comme un effet moyen. Cette approximation est nommée principe du champ moyen. La méthode Hartree-Fock tire avantage de cette simplification en l’appliquant aux électrons d’une molécule. Cependant, les équations de Hartree-Fock sont trop complexes pour permettre une résolution directe par des techniques d’analyse numérique. Il est donc nécessaire d’effectuer une approximation supplémentaire qui consiste à exprimer les orbitales moléculaires (OM) comme des combinaisons linéaires de jeux prédéfinis de fonctions monoélectroniques : c’est l’approximation CLOA (Combinaison Linéaire d’Orbitales Atomiques).
En effet, la théorie Hartree-Fock ne tient pas compte de tous les effets de corrélation entre les mouvements des électrons au sein d’un système moléculaire. La corrélation entre deux électrons de spins parallèles – dite de Fermi – est en partie décrite dans les méthodes Hartree-Fock. Outre cette corrélation de Fermi, il existe, par ailleurs, la corrélation de Coulomb due à la répulsion électrostatique entre les électrons. La différence entre les résultats obtenus en Hartree-Fock et ceux issus de la solution exacte de l’équation de Schrödinger est appelée énergie de corrélation. Les méthodes Post HF permettent de traiter les effets de corrélation qui ne sont pas pris en compte dans une approche de type Hartree-Fock. Elles se partagent en deux catégories : les méthodes perturbatives et les méthodes multi-configurationnelles. Selon la méthode, une partie plus ou moins grande de la corrélation pourra être atteinte[6].
La Théorie de la Fonctionnelle de la Densité (DFT)
L’étude détaillée des propriétés électroniques d’un système moléculaire nécessite la prise en compte des effets de corrélation électronique et ce, tout particulièrement, si celui-ci contient des métaux. Les méthodes Hartree-Fock permettent d’intégrer ces effets mais sont souvent lourdes, limitantes quant à la taille de systèmes étudiés et coûteuses. C’est pourquoi, la Théorie de la Fonctionnelle de la Densité ou DFT de l'anglais Density Functionnal Theory, rédigée en 1964 par Pierre Hohenberg, Walter Kohn et Lu Sham a été considérablement développée pour l’étude des systèmes chimiques et s’est imposée comme une alternative performante aux méthodes Hartree-Fock. Initialement conçue et appliquée aux problèmes de l’état solide, plusieurs raisons ont contribué à sa popularité quant aux applications chimiques. Cette théorie inclut dans son formalisme une grande part de corrélation électronique et la méthode peut être appliquée à tout type de système : covalent, ionique ou métallique. Les ressources informatiques requises sont moins importantes que pour les calculs de type Post HF, rendant ainsi accessibles les études des systèmes moléculaires de plus grandes tailles. La DFT repose sur les deux théorèmes de Hohenberg et Kohn. Le premier théorème stipule qu’à une densité électronique donnée correspond une fonction d’onde unique. Le second théorème postule que l’énergie, fonctionnelle de la densité électronique, obéit au principe variationnel. Ainsi, selon les deux théorèmes de Hohenberg et Kohn, on peut connaître totalement l’état d’un système électronique en déterminant sa densité électronique et on peut obtenir la densité électronique de l’état fondamental en minimisant l’énergie du système. L'idée centrale de la DFT est que la seule densité électronique de l'état fondamental du système détermine entièrement les valeurs moyennes des observables, comme l'énergie. La DFT est une théorie parfaitement exacte mais reste inapplicable car le potentiel d'échange-corrélation est inconnu. Il est donc nécessaire d'approximer ce potentiel.
L’approximation la plus simple dans la DFT quantique utilise l’approximation de la densité locale (LDA) où la fonction dépend uniquement de la densité à l’endroit où la fonction est évaluée. Un raffinement supplémentaire est obtenu en considérant l’approximation de gradient généralisée (GGA) qui est toujours locale mais qui prend également en compte le gradient de la densité au même endroit[7].
Approximation locale de la densité (LDA)
L’idée de base de la LDA est qu’il est possible d’estimer l’énergie d’échange-corrélation d’un système inhomogène en utilisant sur des portions infinitésimales les résultats d’un gaz homogène d’électrons de densité égale à la densité locale du système inhomogène. Cette approximation est raisonnable pour un système où la densité varie lentement mais cette condition n’est pas satisfaite en pratique. Cependant, la LDA est étonnamment efficace et son application aux atomes et aux molécules se justifie par le succès de ses applications numériques. De façon générale, la LDA permet de décrire les liaisons covalentes. Cette approximation est aussi adaptée pour étudier les défauts lacunaires en raison d'une meilleure description des surfaces libres. L’approximation de la LDA permet l’obtention de bons résultats mais elle tend à sous-estimer l'énergie d'échange et à surestimer l'énergie de corrélation. Afin de l’améliorer, il faut tenir compte de l’hétérogénéité de la densité électronique. Pour cela, on introduit dans l'énergie d'échange et de corrélation des termes dépendant du gradient de la densité[8].
Approximation du gradient généralisé (GGA)
La plus grande source d’erreur de la LDA provient de l’énergie d’échange qui, comme vu précédemment, est souvent sous-estimée tandis que l’énergie de corrélation est souvent surestimée même si, en valeur absolue, sa contribution à l’énergie totale est plus petite. Ces deux erreurs ont tendance à s’annuler. Pour améliorer la précision des calculs DFT, nous avons besoin de meilleures approximations pour la fonctionnelle d’échange-corrélation. Certains auteurs ont eu l'idée de définir une fonctionnelle de la densité qu'ils ont associée à ses dérivées propres dans le but de prendre en compte l’inhomogénéité du système. Cependant, l'approche GGA n'est pas toujours suffisante pour décrire les différentes propriétés chimiques et physiques des composés. C'est pour cela, à partir de 1960, de nouveaux types de fonctionnelles ont été développées de manière à aller au-delà des résultats fournis par la GGA.
Les méthodes basées sur la DFT sont considérées à l'heure actuelle comme une méthode ab initio par la plupart des scientifiques. Les théorèmes de Hohenberg et Kohn ainsi que le développement amenant aux équations de Kohn et Sham sont parfaitement rigoureux mais la fonctionnelle d'échange-corrélation apparaissant dans les équations rend toutes résolutions exactes impossibles, sa forme analytique étant inconnue. Il est donc nécessaire d'approximer cette fonctionnelle soit en formulant une forme mathématique approchée de la fonctionnelle ou bien en ajustant un certain nombre de données expérimentales. Cette approche étant typique des méthodes semi empiriques, la méthode DFT pourrait donc tout aussi bien être classée dans cette catégorie[9].
Méthodes empiriques/semi-empiriques à l'échelle atomique
Modèle des liaisons fortes ( « Tight Binding »)
Dans ce modèle, l’objectif est d’obtenir les propriétés du solide par le biais des orbitales atomiques. Les électrons sont considérés comme occupant les orbitales standards de leurs atomes et « sautent » entre les atomes pendant la conduction. La représentation des liaisons fortes est appliquée à une grande variété de solides. Ce modèle fonctionne souvent bien dans les matériaux avec un chevauchement limité entre les orbitales atomiques mais aussi limité entre les potentiels sur les atomes voisins[10].
La représentation de Tight-Binding permet de comprendre les fondements de la structure électronique de bandes des solides. Cette représentation consiste à simplifier les interactions entre électrons et celles entre électron et noyau à l’aide d’hypothèses spécifiques d’interactions fortes électron-noyau et de non interactions entre les électrons. Ces hypothèses sont les suivantes :
- Seuls le/les électrons de valence de chaque atome sont pris en compte, les électrons de cœur ne font pas partie du modèle. On considère que ces électrons de cœur sont déjà engagés dans des liaisons covalentes et n’ont pas d’impact sur le modèle.
- Le/les électrons de valence interagissent fortement avec le noyau de l’atome, et sont donc fortement localisés dans l’espace autour de ce noyau.
- Le/les électrons de valence d’atomes différents n’interagissent pas entre eux. Les interactions électron-électron sont négligées.
- Le/les électrons de valence de chaque atome ont une certaine probabilité de sauter d’un atome à un autre (d’un site du solide à un autre), cette probabilité vaut J.
- Les sauts d’électrons sont à comprendre entre 2 plus proches voisins seulement[11].
Cependant, l’hypothèse d’absence d’interactions entre électrons n’est pas réaliste dans la majorité des solides. En particulier, ce sont les interactions entre électrons qui sont à l’origine des propriétés de magnétisme de certains solides. Il faut également prendre en compte les interactions entre électrons dans le hamiltonien représentant le solide ainsi que dans la résolution de l’équation de Schrödinger. Mais ceci est très compliqué à prendre en compte correctement.
La représentation Tight Binding permet de remonter à l’énergie électronique d’un solide. Cette énergie est donnée par la relation de dispersion. Celle-ci peut se démontrer assez simplement dans certains cas. Ainsi, pour un système 1D constitué de N atomes et N électrons, la relation de dispersion est[12] :
E = ε0 − 2Jcos(ka)
ε0 : énergie de l’électron libre donc de l’atome isolé
J : énergie de saut de l’électron vers l’un des sites voisins
a : distance interatomique
k : vecteur d’onde représentant un électron
Dans le cas d’un solide 2D à N atomes et N électrons, elle devient[13] :
E = ε0 − 2Jcos(kxa) − 2Jcos(kya)
kx et ky : composantes du vecteur d’onde k
Il est possible d’étendre ce modèle à des systèmes à 3D mais les bandes électroniques deviennent bien plus complexes, ainsi que leurs représentations sur des graphes. Il n’est pas compliqué d’écrire le terme des interactions entre électrons dans le hamiltonien du système mais il est difficile de le calculer pour résoudre l’équation de Schrödinger.
Il existe cependant des moyens de résoudre l’équation de Schrödinger électronique d’un solide tridimensionnel composé d’un nombre N très grand d’électrons numériquement, par ordinateurs avec des algorithmes numériques implémentés sur des machines parallèles de calculs, en appliquant des représentations comme celles décrites partie 3. Il est alors possible de connaitre des énergies des bandes électroniques et de leurs remplissages, et d’accéder aux propriétés électroniques du système. Ces méthodes permettent aussi de suivre la dynamique des noyaux dans le temps, et donc celle des électrons également. Pour cela, on se place principalement dans la représentation de Born-Oppenheimer, et on résout l’équation de Schrödinger indépendante du temps à chaque pas de la trajectoire, c’est-à-dire après chaque déplacement des noyaux sous l’effet des forces qui leur sont appliquées[14].
Potentiels interatomiques
Les modélisations moléculaires permettent de décrire les matériaux à l’échelle de l’atome en se servant des équations de la mécanique de Newton afin de prédire les propriétés macroscopiques des matériaux en se basant sur les interactions interatomiques. En fonction des variables prises en compte, ces modèles peuvent par exemple prédire les phases cristallines, leur stabilité thermique et leur enthalpie de changement de phase ainsi que leurs propriétés mécaniques. Cette quantité d’informations, additionnée à une visualisation en trois dimensions, permet de mieux appréhender des phénomènes qui sont souvent inobservables expérimentalement.
Les atomes du système sont représentés par une masse, majoritairement celle du noyau atomique, et sont sujets à des interactions avec d’autres atomes qui proviennent surtout de la composante électronique des atomes. Ces interactions sont associées à des forces qui peuvent être dirigées suivant une direction, comme les liaisons covalentes. Elles peuvent également être sans orientation définie comme les liaisons ionique ou métallique. Ces interactions sont des interactions dites de paires, donc entre deux atomes, et sont décrites par une force venant d’une énergie potentielle.
Nous pouvons distinguer les matériaux (métalliques, organiques et céramiques) selon le type de force d’interaction qui lie les atomes.
Dans les métaux, la cohésion entre atomes est permise grâce à la liaison métallique qui agit principalement sur les premiers voisins. Si les atomes sont de la même espèce chimique, ils peuvent être interchangés sans qu’aucune distinction ne soit faite. Ces interactions sont à l’origine de la compacité du cristal à l’état solide mais aussi de la faible viscosité à l’état fondu.
Les céramiques sont essentiellement formées par des ions qui se lient par voie électrostatique. Celle-ci permet des interactions à plus longue distance et une plus grande cohésion pouvant expliquer leurs propriétés comme le module élastique et leur caractère réfractaire.
Pour les matériaux organiques, ce sont les liaisons chimiques fortes qui établissent la structure chimique des molécules. L’organisation du cristal est possible à l’état solide mais par arrangement, des molécules se lient par des liaisons de Van der Waals, qui sont des interactions considérées comme faibles face aux liaisons chimiques[15].
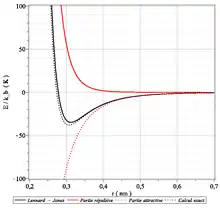
Les potentiels d’interaction contiennent toutes les informations sur la physique et la chimie des atomes et permettent donc d’accéder à diverses propriétés du matériau. Les interactions associées peuvent être modélisées à l’échelle atomique à l’aide de modèles qui peuvent se révéler très réalistes s’ils sont adaptés au système étudié. La liaison covalente peut par exemple être modélisée avec les potentiels REBO ou Tersoff, la liaison métallique avec des potentiels à N-corps EAM ou SMA, la liaison ionique avec des potentiels à charges partielles fixes ou variables comme le potentiel de Vashishta et la liaison Van der Waals avec des potentiels de pair de type Lennard-Jones ou Morse[16].
Un potentiel est composé par deux parties qui s’ajoutent l’une à l’autre. Il y a une composante répulsive qui est dominante lorsque la distance interatomique est faible. L’autre composante est attractive. Concernant la composante répulsive, les noyaux sont suffisamment proches pour que les nuages d'électrons se superposent. La théorie des perturbations ne peut être appliquée et le calcul quantique adopté est celui utilisé pour une quasi-molécule. Les forces à son origine sont les forces coulombiennes et l'interaction d'échange.
Quant à la composante attractive, la théorie des perturbations est cette fois-ci applicable. Dans la partie r<0.5nm, l'interaction d'échange est dominante. C’est dans cette partie que l’on trouve le minimum du potentiel. Dans la région externe l'opérateur d'interaction peut être développé. Une série multipolaire peut être employée pour l’opérateur de l’interaction au sein de la région externe, correspondant alors à des forces de van der Waals. Le terme en r-6 de la série correspond au dipôle mutuellement induit, il s’agit des forces de London. Ce terme se retrouve dans plusieurs potentiels comme le potentiel de Lennard-Jones, de Buckingham et d’autres. Les termes en r-8 représentent les interactions entre dipôles induits-quadripôles induits et sont souvent négligés. Les potentiels d’interaction contiennent toutes les informations sur la physique et la chimie des atomes et permettent donc d’accéder à diverses propriétés du matériau[17].
Méthodes de simulation atomistique
Dynamique moléculaire
La dynamique moléculaire est une méthode déterministe qui consiste à étudier les trajectoires temporelles d'un système d'atomes en interaction, en appliquant les lois de la mécanique newtonienne. Chaque particule est considérée comme une masse ponctuelle dont le mouvement est déterminé par l'ensemble des forces exercées sur elle par les autres atomes.
Les lois du mouvement de Newton sont les suivantes :
- Un corps se déplace en ligne droite à moins qu'une force agisse dessus ;
- La force est égale à la masse fois l'accélération ;
- À chaque action, il existe une réaction égale [18].
La dynamique moléculaire classique sert à :
- Simuler le comportement de systèmes d'atomes en fonction du temps ;
- Simuler les fluctuations autour d'un minimum local ;
- Passer d'un minimum d'énergie à un autre sous l'effet d'un potentiel, d'une contrainte ;
- Suivre l'évolution du système composé de plusieurs particules [19].
Cette méthode est divisée en deux étapes :
- L'implémentation d'un modèle énergétique, permettant de calculer l'énergie totale E d'interaction du système. Ceci permet de déterminer les forces Fi s'exerçant sur chaque atome de coordonnées ri(xi,yi,zi) de masse mi au temps t ;
- L'implémentation et la résolution d'un modèle cinétique, précisément l'intégration des équations de Newton. Au temps t, chaque atome i subit une accélération yi reliée à la force [20].
Pour observer un phénomène de dynamique moléculaire, suivre les fluctuations de structure et mesurer leur fréquence, il faut utiliser une méthode dont le temps caractéristique c'est-à-dire le temps qui lui faut pour réagir à la présence des atomes dans une structure moléculaire donnée et de les observer, soit comparable à la durée du mouvement que l'on veut étudier. Si ce temps est très court par rapport au phénomène, on ne peut avoir une structure de la molécule qu'à un instant figé. C'est le cas des spectroscopies Infrarouge et Ultraviolette [21].
Il existe deux types de dynamique :
- La dynamique dans le vide ;
- La dynamique en présence de solvant.
Les avantages de la dynamique dans le vide sont les suivants :
- Grande simplicité;
- Grande rapidité de calcul;
- Permet un temps de dynamique plus long.
Les avantages de la dynamique en présence de solvant sont les suivants :
- Meilleure prise en compte de l'effet électrostatique ;
- Possibilité de formation de la liaison hydrogène avec le solvant ;
- Prise en compte(partielle) de l'effet hydrophobe ;
- Meilleure stabilité du système [22].
Méthode de Monte-Carlo
La méthode de Monte-Carlo est une méthode numérique qui permet de reconstituer artificiellement un phénomène aléatoire en simulant un échantillon fictif de réalisations à partir d'hypothèses sur les variables aléatoires.
L'objectif est de générer un ensemble de configurations représentant le système afin de calculer les grandeurs thermodynamiques par une estimation de la valeur moyenne sur les configurations générées.
La méthode de simulation de Monte-Carlo fournit une gamme de résultats possibles. Ainsi, pour chaque résultat, nous pouvons déterminer la probabilité qu'il se produise. Cette technique est souvent utilisée dans les domaines suivants:
- la finance;
- les mathématiques;
- la physique;
- la biologie moléculaire et génétique.
La méthode de Monte-Carlo offre un certain nombre d'avantages:
- Les résultats permettent de prédire ce qui pourrait arriver ;
- Elle permet d'avoir une estimation sur l'erreur ;
- Il est facile de déterminer quelles valeurs ont le plus d’intérêt sur les résultats [23].
Méthode de Metropolis
La méthode de Monte-Carlo Metropolis a été introduite en physique de la matière condensée par Metropolis. Sa mise en œuvre nécessite de parcourir l'espace des configurations et un modèle de calcul d'énergies des configurations.
Cette méthode tient une place spéciale en modélisation moléculaire. Elle a été utilisée pour réaliser la première simulation informatique d'un système moléculaire.
Elle génère de manière aléatoire un grand nombre d'échantillons d'un système moléculaire (et donc de son énergie) afin d'en explorer la surface d'énergie potentielle.
Cependant une génération purement aléatoire de conformations ne permet pas de distinguer les conformations de hautes et basses énergies. Elles seront générées avec la même probabilité. D'un point de vue chimique, cela correspond à échantillonner des structures avec une haute énergie ayant peu de sens physique avec la même probabilité que les structures physiquement réalistes.
Ce concept est illustré par des notions de mécanique statistique.
La mécanique statistique permet de prédire les propriétés macroscopiques d'un système sur la base des propriétés individuelles de ses constituants microscopiques [24].
La première étape de cette méthode consiste en la construction de chaines de Markov. Une chaîne de Markov est une suite de variables aléatoires qui permet de modéliser l'évolution dynamique d’un système aléatoire. La propriété fondamentale des chaînes de Markov est que son évolution future ne dépend du passé qu’au travers de sa valeur actuelle [25].
La chaîne construite est de type :
Une Chaîne de Markov doit être ergodique. C'est-à-dire que le nombre de déplacements acceptés quittant l'état i doit être exactement égal au nombre de déplacements conduisant à l'état i à partir de tous les autres états. La seconde étape consiste en la réalisation de l'algorithme.
L'algorithme de Metropolis présente certaines limites :
- Le taux de rejet lors du tirage des transitions peut être élevé, ce qui peut ralentir l'évolution du processus;
- Le temps pris en compte est un nombre d'itérations et ne correspond pas à un temps réel.
Le principe général de cette simulation peut être décrit de la manière suivante :
- Calculer l'énergie du système dans son état n, Un
- Effectuer un changement aléatoire pour obtenir la conformation n+1
- Calculer l'énergie du système dans son état n+1, Un+1
- Effectuer le test d'acceptabilité
- Retourner au numéro 1 avec la nouvelle conformation (n+1)
Le test d'acceptabilité est le suivant :
- Si Un+1 est inférieur ou égal à Un accepter le changement et garder la conformation n+1. Elle sera comptabilisée dans la statistique de la simulation.
- Si Un+1 est supérieur à Un, évaluer le changement selon l'équation :
- Il s'agit de tirer un nombre aléatoirement entre 0 et 1. Si ce nombre est inférieur à U rejeter le changement et garder la conformation n. Si ce nombre est supérieur à U accepter le changement et garder la conformation n+1. Ceci permet au protocole de donner une chance de tirage à des structures de plus haute énergie.
- Collecter les variables et les faire contribuer à la moyenne globale.
Méthode de Monte-Carlo Cinétique

La méthode de Monte-Carlo Cinétique est une méthode de Monte-Carlo permettant de simuler l'évolution d'un système qui est le siège de processus se produisant à des vitesses connues. Elle permet de gérer un temps qui peut être relié au temps expérimental, permettant ainsi une comparaison avec les cinétiques expérimentales.
Contrairement à la méthode de Métropolis dans laquelle les évolutions sont liées à des variations aléatoires des positions qui n'ont pas nécessairement de sens physique précis, cette méthode est basée sur le recensement des processus physiques élémentaires pouvant se produire dans le système.
Chacun de ces processus i est associé à une énergie d'activation Ei et une vitesse vi [20].
L'équation maîtresse est la suivante :
Avec :
W(i,t) : probabilité du système d'être dans la configuration i au temps t ;
P(i→j) : probabilité de transiter d'une configuration i au temps t vers une configuration j à t+1
La probabilité d'une transition est obtenue par le rapport entre la vitesse du processus associé à cette transition et la somme des vitesses des processus de toutes les transitions possible de la configuration :
Les algorithmes les plus utilisés pour cette méthode sont les suivants :
- Algorithme Primaire ou simple;
- Algorithme Bortz-Kalos-Liebowitz (BKL);
- Algorithme Bortz-Kalos-Liebowitz (BKL) par méthode des classes.
Le point commun de ces algorithmes repose sur le calcul des probabilités de transition, et le calcul du temps. La différence concerne le choix du processus élémentaire à réaliser à chaque étape de l'algorithme.
L'algorithme Monte-Carlo cinétique est utilisé pour simuler les phénomènes physiques tels que la diffusion de surface, l'épitaxie, l'évolution et la croissance de domaines ou la mobilité des agrégats.
Enjeux socio-économiques
La modélisation fournit également des prédictions inestimables sur l’évolution d’un système d’une manière plus rapide ou moins coûteuse qu’avec des méthodes d’essai et d’erreur. L’industrie utilise la modélisation pour :
- Réduire les coûts en établissant une stratégie de mise à l’essai et en présélectionnant les nouveaux candidats au matériel, lorsqu’une approche « d’essai et d’échec » ne peut être mise en œuvre dans l’industrie ou que ce serait trop compliqué, dangereux ou coûteux.
- Comprendre les résultats des mesures. Ceci est particulièrement important à l’échelle nanométrique et femtométrique où l’accès aux propriétés des matériaux et aux méthodes de traitement est souvent difficile. La simulation peut fournir cette information pour chaque point de l’échantillon à tout moment. Réduire le temps de mise sur le marché, en accélérant les délais de compréhension et de développement de nouveaux matériaux et de matériaux existants dans de nouvelles applications.
- Suggérer de nouveaux matériaux et des procédures expérimentales pour les créer. La conception des matériaux par modélisation consiste à étudier les relations entre la composition chimique et physique, la microstructure et les propriétés efficaces à l’échelle macroscopique, de sorte qu’un matériau peut être conçu avec les macro-propriétés souhaitées. La modélisation peut être utilisée pour examiner les propriétés des matériaux et des dispositifs qui n’ont pas été créés ou qui ne le sont pas encore.Le développement de moyens de calculs puissants à coût modéré permet à la modélisation moléculaire de prendre en compte des systèmes de plus en plus réalistes[26].
Au cours de ces 15 dernières années, elle a permis d'abaisser considérablement le temps de calcul et le coût des opérations. Cependant, au fil des découvertes, le coût a généralement augmenté mais une plus large gamme de systèmes a pu être analysée, de manière plus rentable, en combinant expérience et simulation.
Elle permet de comprendre le comportement et la structure de nombreux systèmes et souvent de prédire des propriétés importantes pour les chercheurs et ingénieurs. L'essor de la modélisation moléculaire provient de l'évolution de calculateurs et du développement des algorithmes rapides. Les codes de calculs sont distribués mondialement. La commercialisation des logiciels facilitant l'utilisation dans l'industrie contribuent également à l'essor mondial de cette discipline.
La modélisation moléculaire participe profite à différents secteurs dont l'énergie et l'environnement en augmentant l'efficacité énergétique dans les transports ou encore dans les bâtiments, développer des énergies renouvelables telles que les biocarburants ou encore l'hydraulique.
En ingénierie, les simulations atomistiques sont devenues indispensables. Une communication de la Commission européenne sur les infrastructures indique que la fabrication d'objets complexes comme les avions ou encore les voitures sont basées sur la modélisation.
Les simulations basées sur des modèles moléculaires ont d'abord eu un impact dans le secteur des sciences de la vie. De plus, elle représente un élément essentiel dans le domaine de la pharmaceutique [27].
La simulation atomistique est une discipline à part entière de la chimie, possédant ses congrès, ses sociétés de services spécialisées ainsi que ses revues [28].
Références
- (en) Anne F. de Baas, Lulla Rosso, What Makes a Material Function? : Let Me Compute the Ways : Modelling in FP7 NMP Programme Materials ProjectsVolume 25531 de EUR (Luxembourg. Online), ISSN 1831-9424, , 255 p. (lire en ligne), p. 6-7
- CEA Grenoble, DSM/DRFMC. Disponible sur : « Approche multi-échelles en simulation atomistique », (consulté le ).
- INAC. « Simulation atomistique en science des matériaux : des propriétés physiques aux nanostructures », sur http://inac.cea.fr, (consulté le ).
- Julien Godet, Etude par simulations et calculs atomistiques, de laformation de dislocations aux défauts de surface dans un cristal de silicium soumis à des contraintes, , 177 p. (lire en ligne).
- Maylis Orio, Etude par la Théorie de la Fonctionnelle de la Densité des propriétés électroniques et magnétiques de complexes de fer. Application aux systèmes de types Catalase et Fer-Soufre, Grenoble, , 361 p. (lire en ligne), p. 4
- Maylis Orio, Etude par la Théorie de la Fonctionnelle de la Densité des propriétés électroniques et magnétiques de complexes de fer. Application aux systèmes de types Catalase et Fer-Soufre, Grenoble, , 361 p. (lire en ligne), p. 5
- Maylis Orio, Etude par la Théorie de la Fonctionnelle de la Densité des propriétés électroniques et magnétiques de complexes de fer. Application aux systèmes de types Catalase et Fer-Soufr, Grenoble, , 361 p. (lire en ligne), p. 15
- Maylis Orio, Etude par la Théorie de la Fonctionnelle de la Densité des propriétés électroniques et magnétiques de complexes de fer. Application aux systèmes de types Catalase et Fer-Soufr, Grenoble, , 361 p. (lire en ligne), p. 21
- Maylis Orio, Etude par la Théorie de la Fonctionnelle de la Densité des propriétés électroniques et magnétiques de complexes de fer. Application aux systèmes de types Catalase et Fer-Soufre, Grenoble, , 361 p. (lire en ligne), p. 22
- (en) Anne F de Baas, What makes a material function ? Let me compute the ways…, , 384 p. (lire en ligne), p. 22
- M.P. Gaigeot, Représentation ’Tight Binding’ (liaisons fortes) etstructure électronique de bandes des solides.Au-delà des électrons indépendants., , 20 p. (lire en ligne), p. 1-2
- M.P. Gaigeot, Représentation ’Tight Binding’ (liaisons fortes) et structure électronique de bandes des solides. Au-delà des électrons indépendants., , 20 p. (lire en ligne), p. 5
- M.P. Gaigeot, Représentation ’Tight Binding’ (liaisons fortes) et structure électronique de bandes des solides. Au-delà des électrons indépendants., , 20 p. (lire en ligne), p. 13
- M.P. Gaigeot, Représentation ’Tight Binding’ (liaisons fortes) et structure électronique de bandes des solides. Au-delà des électrons indépendants., , 20 p. (lire en ligne), p. 16-17
- B. Monasse, CHAPITRE XXVIII : MODELISATION MOLECULAIRE DES MATERIAUX, 9 p. (lire en ligne), p. 1-2
- E. Despiau-Pujo, Principes de la Dynamique Moléculaire, Grenoble, , 31 p. (lire en ligne), p. 10-14
- (en) Ilya G. Kaplan, Intermolecular Interactions. Physical Picture, Computational Methods and Model Potentials, (lire en ligne)
- « Modélisation moléculaire », (consulté le ).
- LAAS-CNRS.« Méthodes cinétiques atomistiques », (consulté le ).
- Yves Alain Beh Ongueng, Simulation atomistique Monte Carlo cinétique, , 212 p. (lire en ligne).
- Riess Jean. « Dynamique moléculaire ». Encyclopædia Universalis [en ligne], consulté le 22 septembre 2019
- « Cours Modélisation à partir de données expérimentales de RMN ».
- PALISADE. Disponible sur : « Monte Carlo simulation ».
- Université en ligne. Disponible sur : « Le principe de l'approche Monte Carlo Metropolis » (consulté le ).
- CERMICS. Introduction aux chaines de Markov, 2 p. (lire en ligne).
- (en) Anne F de Baas, What makes a material function ? Let me compute the ways…, , 384 p. (lire en ligne), p. 6-9
- Gerhard Goldbeck. The economic impact of the molecular modelling, (lire en ligne).
- Frédéric Biscay, Céline Chizallet, Benoit Creton, Antoine Fecant, Nicolas Ferrando, Patrice Malfreyt, Carlos Nieto-Draghi, Pascal Raybaud, Christhiane Rousseau et Philippe Ungerer, « La modélisation moléculaire s’invite dans l’industrie », L'Actualité chimique, vol. 2, (lire en ligne).




