Réseaux de Kahn
Les réseaux de Kahn (en anglais, Kahn process networks souvent abrégé KPNs, ou plus simplement process networks) sont un modèle de calcul distribué dans lequel un groupe de processus déterministes communiquent entre eux à travers des files non bornées. Le réseau ainsi constitué a un comportement déterministe indépendant des différents temps de calcul ou de la latence des échanges de message. Bien que le modèle ait été initialement développé pour modéliser les systèmes distribués, il s’est révélé adéquat pour modéliser des systèmes de traitement du signal. En conséquence, les réseaux de Kahn sont utilisés pour modéliser les systèmes embarqués et les systèmes distribués (notamment pour le calcul haute-performance). Les réseaux sont nommés d’après Gilles Kahn qui les a décrits en 1974 dans un article intitulé The semantics of a simple language for parallel programming[1] (littéralement : la sémantique d’un langage simple pour le calcul parallèle).
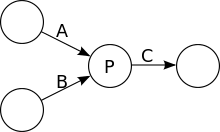
Modèle d’exécution
Les réseaux de Kahn sont un modèle standard pour décrire des systèmes de traitement du signal où les données en flux continu sont traitées séquentiellement par des processus s’exécutant en parallèle. Du fait que chaque processus est indépendant et que son comportement ne dépend que de l’état de ses canaux de communication, exécuter le modèle ne nécessite pas de parallélisme physique ou de système à temps partagé.
Dans le modèle, les processus communiquent à l’aide de files de messages non bornées. Les processus lisent et écrivent des données atomiques. L’écriture dans une file n’est pas bloquante, puisque les files sont infinies. En revanche, lire sur une file vide est bloquant. Un processus lisant sur une file vide est donc bloqué tant qu’il n’y a pas de donnée disponible. Les processus ne peuvent pas tester si une file est vide ou non, avant d’essayer de lire dedans, ce critère garantit le déterminisme quel que soit l’ordre d’exécution des processus. Pour un historique de données donné, un processus doit être déterministe, de sorte qu’il produise les mêmes sorties en fonction des entrées. Ainsi, le temps ou ordre d’exécution des processus ne peut pas modifier le résultat de chaque processus et le comportement global du réseau.
Cas particuliers
- Un processus peut ne pas avoir d’entrées, ou ne rien lire de ses entrées, il agit en ce cas en tant que source pure de données ;
- Un processus peut ne pas avoir de sorties, ou ne pas écrire sur ses sorties ;
- Tester si une entrée est vide peut être autorisé pour des raisons d’optimisation, à la condition expresse que ça ne modifie pas les sorties. Par exemple, un processus doit lire l’entrée 1, puis l’entrée 2, avant d’écrire sa sortie. S’il sait que la file 1 est vide mais que la 2 est prête, il peut gagner du temps en lisant d’abord la valeur de la file 2 avant d’être bloqué en lecture de la file 1. Cela peut permettre de gagner du temps notamment si le temps de lecture est long (allocation de ressources par exemple).
Lien avec les réseaux de Petri
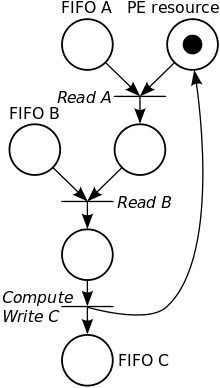
Prenons le réseau schématisé dans l’introduction. Supposons que le processus P est constitué de sorte qu’il lise d’abord sur l’entrée A (FIFO A), puis sur B, qu’il calcule quelque chose avec les deux données, puis l’écrit sur la sortie C, puis recommence. On peut modéliser ce comportement à l’aide du réseau de Petri présenté ci-contre. Le jeton situé dans la place PE resource force une exécution séquentielle du réseau de Kahn. Lorsque des données arrivent via les entrées A ou B, des jetons sont placés respectivement dans les places FIFO A et FIFO B. La transition Read A peut-être effectué lorsqu’il y a au moins un jeton dans FIFO A et un jeton dans PE resource. Le résultat de la transition rempli la place nécessaire à la transition Read B suivant le même principe. La dernière transition Compute/Write C correspond au calcul du processus P et à l’écriture sur sa sortie C. Le franchissement de cette dernière transition rempli à nouveau la place PE resource, permettant de franchir à nouveau la transition Read A dès qu’un jeton est disponible dans FIFO A.
Lien avec les automates finis
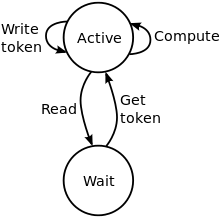
Un processus de Kahn peut être modélisé à l’aide d’un automate fini de deux états, dont le schéma est donné ci-contre :
- Active (en cours) : le processus calcule ou écrit sur une de ses sorties ;
- Wait (en attente) : le processus est bloqué en lecture sur une entrée.
En supposant que l’automate lise des données correspondant au comportement du processus, il pourrait donc lire trois types d’éléments Compute (calculer), Read (lire) et Write token (écrire). Une lecture le mène forcément dans l’état Wait, duquel il ne peut sortir qu’en lisant Get token, signifiant que le canal de communication contient au moins une valeur.
Propriétés
Bornes des files
Une file est strictement bornée par s’il y a au plus éléments dans cette file pour toutes les exécutions possibles. Un réseau est strictement borné par si toutes les files sont strictement bornées par .
Le nombre de données en attente dépend de l’ordre d’exécution des processus. Une source spontanée de données peut produire une quantité arbitraire de données dans une file si l’ordonnanceur n’exécute pas les processus pour en consommer.
Une application concrète ne peut pas avoir de files non bornées. Une implémentation doit donc calculer l’ordonnancement des processus afin d’établir une limite maximale de taille de file. Le problème de la capacité peut-être géré de différentes façons :
- Les limites de file peuvent être dérivées mathématiquement lors de la conception pour éviter les débordements de file. Cependant cette méthode n’est pas applicable pour tous les réseaux. Déterminer la valeur pour laquelle un réseau est strictement borné est indécidable. De plus, les capacités nécessaires peuvent dépendre du type de données à traiter.
- La capacité des files peut grandir lorsque c’est nécessaire (Parks 1995).
- Il est possible de rendre l’écriture bloquante lorsqu’une file est pleine. Cependant cette approche peut mener à des interblocages artificiels, à moins que le concepteur du réseau n'ait correctement calculé les limites sûres des files (Parks 1995). Une détection locale lors de l’exécution peut être nécessaire pour garantir des sorties correctes (Geilen et Basten 2003).
Réseaux ouverts et fermés
Un réseau fermé est un réseau dans lequel il n’y a pas d’entrée ou de sortie externes. Toutes les files sont connectées à deux processus. Les processus n’ayant pas d’entrée sont des producteurs, et ceux n’ayant pas de sortie, des consommateurs.
Un réseau ouvert est un réseau dans lequel tous les processus ont au moins une entrée et une sortie.
Déterminisme
Les processus d’un réseau de Kahn sont déterministes. Pour la même séquence de données dans ses entrées, un processus produira la même séquence de sortie. Les processus peuvent être modélisés comme des programmes séquentiels qui lisent et écrivent dans des canaux dans n’importe quel ordre et pour n’importe quelle quantité de données, tant que la propriété de déterminisme est préservée. Le modèle des réseaux de Kahn est déterministe de sorte que les sorties du système sont déterminées par le comportement des processus, le schéma du réseau et les valeurs initiales. Ni le temps de calcul propre à chaque processus, ni la latence des files de communication n’interviennent dans la caractérisation de déterminisme.
Monotonie
Les réseaux de Kahn sont monotones, ils n’ont besoin que de données partielles depuis leurs entrées pour produire des données partielles en sortie. La monotonie permet le parallélisme, car les processus sont de simple fonctions des entrées vers les sorties.
Utilisations
De par sa simplicité et sa grande expressivité, les réseaux de Kahn sont utilisés comme support à des modèles de calculs dans différents outils théoriques, notamment pour des calculs orientés sur des flux de données.
L’université de Leyde développe un framework open source nommé Daedalus[2] qui transforme des programmes séquentiels écrit en C en réseaux de Kahn. Cette transformation permet de transposer un programme logiciel en circuit, par exemple pour un FPGA.
Le processeur Ambric Am2045 utilise en interne un modèle de calcul comparable aux réseaux de Kahn[3]. Il possède une architecture parallèle composée de 336 cœurs reliés entre eux par des files dont les connexions sont programmables. Ces files sont bornées à l'aide des écritures bloquantes.
Notes et références
- (en) Gilles Kahn, « The semantics of a simple language for parallel programming », Proceedings of IFIP Congress, vol. 6, , p. 471-475 (ISBN 0-7204-2803-3, lire en ligne, consulté le )
- Daedalus (framework)
- (en) M. Butts, A.M. Jones et P. Wasson, « A Structural Object Programming Model, Architecture, Chip and Tools for Reconfigurable Computing », Proceedings of Field-Programmable Custom Computing Machines, vol. 15, , p. 55-64 (ISBN 978-0-7695-2940-0, DOI 10.1109/FCCM.2007.7)
