Réseaux d'interactions mutualistes

La diversité est un facteur important de la structure d’un réseau d’interactions écologiques. Elle correspond au nombre d'espèces présentes dans le réseau.

À partir de cette valeur, il est possible de calculer la taille du réseau qui est le produit du nombre total d’espèces animales et du nombre total d’espèces végétales interagissant dans le réseau[7].

Ce facteur permet de mieux représenter les interactions entre espèces plutôt que les espèces elles-mêmes.

La connectance est le nombre d’interactions observées par rapport au nombre total d’interactions possibles[5].

Elle peut être calculée par la formule[7]:

${\displaystyle C={\frac {I{\scriptstyle {\text{observées}}}}{I{\scriptstyle {\text{max}}}}}}$

Figure 1. Représentation de la connectance d’un réseau en fonction du nombre d’espèces. Plus une communauté est riche, plus sa connectance est faible.

Avec ${\displaystyle C}$ la connectance,${\displaystyle I{\scriptstyle {\text{observées}}}}$ le nombre d’interactions observées et ${\displaystyle I{\scriptstyle {\text{max}}}}$ le nombre total d’interactions possibles dans le cas où toutes les espèces animales interagissent avec toutes les espèces végétales. La connectance est donc un nombre entre 0 et 1.

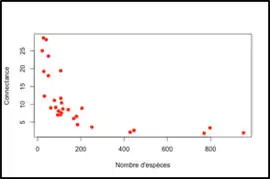
Le nombre absolu d’interactions augmente avec le nombre d’espèces impliquées dans un réseau, donc la diversité de ce réseau. Mais la connectance, quant à elle, diminue avec le nombre d’espèces. Cela est dû au fait qu’une espèce ne réalise jamais toutes les interactions possibles d’un réseau [4].

En considérant cela, il est possible de déduire une autre manière de calculer la connectance[8] - [9]:

${\displaystyle C={\frac {I{\scriptstyle {\text{observées}}}}{S^{2}}}}$

Avec ${\displaystyle S}$ est la richesse spécifique du réseau.

Ainsi, une connectance faible indique, par exemple, qu’un individu particulier du réseau réalise peu d’interactions par rapport à toutes les interactions du réseau.

Les altérations d’un réseau sont en partie liées à des modifications de la diversité et de la connectance[5].

Figure 2. Représentation d’une matrice de modularité pour un réseau plantes-pollinisateurs à 16 espèces et 16 interactions. Les carrés pleins correspondent à l'interaction entre 2 espèces, et les encadrements font référence aux modules du réseau. Ainsi, la matrice montre 4 modules, chacun composé de 4 espèces interagissant fortement entre elles (2 espèces de plantes et 2 espèces de pollinisateurs).

La modularité caractérise le degré de compartimentation d’un réseau[5] en modules. Un module est composé d’espèces interagissant fortement entre elles, et faiblement avec les espèces externes à ce module[6].

Un réseau modulaire peut être le résultat d’espèces proches phylogénétiquement ou d’un habitat hétérogène, conduisant ainsi à des interactions non aléatoires et complexes au sein du réseau[10].

Cependant, ce paramètre peut être difficile à quantifier face aux manques d’algorithmes suffisamment puissants pour détecter l’ensemble des modules[10].

Il est possible de mesurer la modularité par la formule[11]:

${\displaystyle M=\sum _{s=1}^{N_{M}}\left[{\frac {l{\scriptstyle {\text{s}}}}{L}}-\left({\frac {d{\scriptstyle {\text{s}}}}{2L}}\right)^{2}\right]}$

Dans cette formule :

${\displaystyle N_{M}}$ = nombre de modules

${\displaystyle L}$ = nombre de liens dans le réseau

${\displaystyle l_{s}}$ = nombre de liens entre la totalité des espèces du module ${\displaystyle s}$

${\displaystyle ds}$ = nombre de liens total des espèces du module au sein de celui-ci et avec les autres modules.

Dans ce calcul, ${\displaystyle M}$ mesure donc la modularité. Dans le cas d’un réseau parfaitement modulaire, ${\displaystyle M}$ prendra la valeur de 0. Et à l’inverse, dans le cas d’un réseau très peu modulaire, ${\displaystyle M}$ tendra vers ${\displaystyle -{\frac {1}{N_{M}}}}$.

Figure 3. Matrices représentant un réseau d’interactions entre 18 espèces classées en fonction de leur degré de généralisation. Les carrés verts représentent les 45 interactions entre 9 espèces de pollinisateurs et 9 espèces de plantes, classées de la plus généraliste (rang 1) à la moins généraliste (rang 9). La droite rouge correspond à l’isocline de parfaite nestedness. La figure a. représente un réseau à nestedness parfaite, la figure b. un réseau à nestedness plus faible. Dans le cas d’une parfaite nestedness, aucune interaction entre deux espèces spécialistes n’est observable. Plus précisément, les espèces de rang 6 ou supérieur n’interagissent jamais entre elles, mais sont en interaction avec les espèces les plus généralistes.

La nestedness, aussi appelée imbrication ou emboîtement, est caractérisée par des interactions entre espèces généralistes-généralistes et spécialistes-généraliste principalement, les interactions entre deux espèces spécialistes étant peu fréquentes[12] ; on parle alors de spécialisation asymétrique.

Un réseau d’interactions plantes-pollinisateurs avec une nestedness parfaite peut être représenté comme sur la figure 3. Un tel réseau présente premièrement un ensemble d’espèces de plantes et de pollinisateurs généralistes interagissant tous entre eux (carrés vert foncé), induisant ainsi une redondance fonctionnelle au sein du réseau. De ce fait, si l’une des espèces impliquées disparaît, l’interaction perdue pourra être compensée par les autres espèces généralistes[13]. De plus, aucune interaction entre deux espèces spécialistes n’est observable. A ajouter que la modularité est corrélée négativement avec la nestedness[6], ce qui concorde avec le fait que les réseaux d’interactions mutualistes sont fortement imbriqués et peu modulaires.

De nombreuses mesures ont été proposées pour quantifier la nestedness au sein des réseaux d’interactions mutualistes. Parmi ces propositions, deux sont particulièrement utilisées: la température ${\displaystyle T}$ [14] et la NODF[15] (Nestedness metric based on Overlap and Decreasing Fill). Il est cependant important de noter que le choix des métriques ne se fait pas au hasard, celui-ci dépend de ce qui est testé : nestedness de la composition en espèces ou de l’incidence des espèces[16]. De plus, ces formules peuvent être vouées à de multiples modifications, comme ça a été le cas avec la mesure de la température T proposée pour la première fois par Atmar et Patterson en 1993 et pour laquelle des modifications ont été suggérées par Rodriguez-Girones et Santamaria en 2006.

Figure 4. Représentation de la force et l’asymétrie des interactions. La force des interactions est représentée par l’épaisseur des flèches. La majorité des espèces présente des interactions faibles avec les autres espèces.

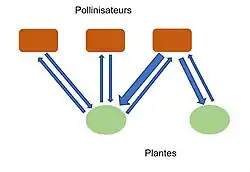
Pour étudier la structure de ces réseaux, deux notions également importantes sont la force et l’asymétrie des liens. En effet les liens unissant deux espèces peuvent être plus ou moins fort. La force des liens peut être représentée par l’impact d’une espèce sur la fitness de l’autre. Et l’asymétrie peut être observée en comparant l’impact de deux espèces l’une sur l’autre. Si une espèce a un impact plus fort sur l’autre alors la relation est asymétrique. En pratique, la mesure de la force est souvent résumée au nombre d'occurrences de l’interaction entre une espèce et une autre. Cette mesure est pratique mais néglige les différentes intensités que chaque occurrence de l’interaction peut avoir en fonction des espèces (les pollinisateurs ne vont pas tous transmettre le pollen aussi efficacement)[17].

Figure 5. Schéma d’un réseau mutualiste simplifié plante-pollinisateur. Les chiffres dans les figures représentent le degree de chaque nœud, c’est-à-dire le nombre d’interactions que fait l’espèce. On retrouve une structure hétérogène, avec des spécialistes et un nœud de généralistes et imbriquée, avec les spécialistes qui interagissent avec un sous-ensemble des espèces avec qui les généralistes interagissent.

Dans la nature, la majorité des réseaux d’interaction plantes-pollinisateurs et plantes-frugivores sont des réseaux :

• hétérogènes: la majorité des espèces présente peu d’interactions, mais quelques-unes ont de nombreuses connexions, il s’agit d’un noyau de généralistes
• imbriqués: les espèces spécialistes interagissent avec des sous-groupes des espèces avec lesquelles des généralistes interagissent
• construits sur des interactions faibles et asymétriques : les espèces au sein d’une paire ne dépendent pas fortement l’une de l’autre. Dans le cas où l’interaction est forte, elle est souvent unilatérale, c’est-à-dire qu’un des partenaires dépend beaucoup de l’autre, mais ce n’est pas réciproque[17].

Ce qui a été décrit précédemment considère que les interactions dans le réseau sont toutes mutualistes et à bénéfices réciproques. Or, la réalité est bien plus complexe et les interactions dans un réseau beaucoup plus diverses. Dans le cas du mutualisme, on peut notamment s’intéresser à un cas récurrent qui est celui de la présence de tricheurs. Ici, la triche est définie comme l’exploitation par une espèce d’une interaction mutualiste sans apporter de gain de fitness, et donc de bénéfices, aux autres espèces[2]. Par exemple, dans le cas des interactions plantes-pollinisateurs, ces tricheurs peuvent être des organismes non-mutualistes qui vont chercher à récupérer la récompense de l’interaction (nectar et pollen par exemple), sans rien donner en retour[18]. Ces organismes représentent un coût obligatoire du mutualisme pour les espèces impliquées. De plus, l’augmentation du nombre d’espèces dans un réseau mutualiste entraîne un accroissement de la proportion de tricheurs[2].

L’étude réalisée en 2010 par Genini et collaborateurs[18] a cherché à comprendre l’impact des tricheurs sur la structure des réseaux d’interactions mutualistes. Elle se base sur les réseaux plantes-animaux de deux familles de plantes tropicales: les Malpighiaceae et les Bignoniaceae dont les fleurs sont plus diverses et donc attirent un plus grand éventail de visiteurs tels que des insectes, des oiseaux ou des chauves-souris. Les résultats montrent que les tricheurs sont bien plus communs (75% des visiteurs) au sein du réseau des Bignoniaceae, qui est donc majoritairement un réseau plantes-tricheurs, qu’au sein de celui des Malpighiaceae (25% des visiteurs) qui est principalement mutualiste. Selon Genini et ses collaborateurs, cette différence dans la proportion des tricheurs peut expliquer la structure du réseau. En effet, le réseau de Malpighiceae est imbriqué mais non modulaire, tandis que celui des Bignoniaceae est modulaire mais non imbriqué. Ainsi, une augmentation de la tricherie dans un réseau d’interactions mutualistes peut entraîner une baisse de la nestedness et une augmentation de la modularité. En effet, la triche par vol de pollen est équivalente à l’herbivorie, dont les réseaux sont fortement modulaires[18]. De plus, ils ont également observé lors de cette étude que le retrait des tricheurs du réseau des Bignoniaceae a entraîné une diminution importante de la modularité, tandis que leur retrait du réseau des Malpighiceae n’a eu aucun impact conséquent.

On peut alors penser que les tricheurs ont seulement un impact négatif sur la stabilité des réseaux mutualistes, en réduisant la nestedness qui renforce le réseau. Cependant, il est possible que la modularité réduise la progression d’une perturbation dans le réseau. Ainsi, les tricheurs, qui sont ubiquistes dans le mutualisme, semblent jouer un rôle important dans la stabilité et la structure de ces réseaux[18].

Le mutualisme est une interaction coévolutive. De ce fait, la structure des réseaux mutualistes n’est pas issue de processus aléatoires non explicables, mais elle est le résultat d’une sélection coévolutive[2] - [3]. Deux forces de coévolution agissent pour former un réseau spécialisé autour d’un noyau de traits mutualistes: la complémentarité et la convergence[13] - [3]. Pour la complémentarité, une interaction mutualiste entre deux espèces, par exemple une plante et son pollinisateur, va se construire sur la complémentarité de traits phénotypiques qui influencent la fitness résultante de l’interaction entre les deux partenaires. La complémentarité entre la longueur de la langue d’un pollinisateur et celle de la corolle de la fleur est un bon exemple. Cette notion est la clé du succès ou de l’échec de l’interaction mutualiste entre une plante et un animal. Une fois cette interaction définie, d’autres espèces non apparentées vont pouvoir venir se greffer au réseau par convergence des traits[3]. On peut alors parler de coévolution diffuse. C’est un phénomène de coévolution qui s’observe au sein d’un groupe d’espèces en interaction, et qui peut affecter l’ensemble du réseau, en raison des pressions sélectives qui s’exercent et des réponses évolutives réciproques entre les espèces. Cette coévolution diffuse peut se mettre en place dans les réseaux d’interactions mutualistes, par exemple plantes-pollinisateurs. C’est ce qui explique la convergence coévolutive qui se met en place au sein de ces réseaux. Celle-ci est d’autant plus importante en présence de généralistes qui interagissent avec plusieurs groupes d’espèces[1].

En raison de la complémentarité et de la convergence, le mutualisme semble généralement coévoluer autour d’un noyau de traits mutualistes chez les espèces impliquées dans le réseau[2]. Plus le réseau grandit, plus ce noyau devient une stratégie évolutive stable. Plus la coévolution progresse, plus la sélection agit sur chaque espèce pour maximiser la fitness et minimiser le coût qu’elles tirent des interactions. À partir de tout ça, Thompson écrit dans le chapitre 14 de son livre The Geographic Mosaic of Coevolution une hypothèse sur la convergence au sein des réseaux mutualistes :

« Reciprocal selection on mutualisms between free-living species favors genetically variable, multispecific networks in which species converge and specialize on a core set of mutualistic traits rather than directly on other species. »

« La sélection réciproque qui s’exerce dans le mutualisme entre des espèces libres favorise des réseaux génétiquement variables et plurispécifiques au sein desquels les espèces convergent et se spécialisent autour d’un noyau de traits mutualistes plutôt que directement entre espèces. »

L’évolution de la pollinisation des plantes est un exemple classique d’un tel phénomène. C’est notamment le cas de celles qui sont pollinisées par des papillons de la famille des Sphinx. Ces plantes sont de plusieurs familles différentes et sont de formes variées. Cependant, elles partagent certaines combinaisons de traits qui augmentent la pollinisation par les Sphinx, tels que des fleurs blanches et tubulaires, du nectar composé de saccharose ou encore la déhiscence au crépuscule[2]. De tels traits vont former le noyau autour duquel la coévolution se met en place.

Cette coévolution qui a lieu au sein des réseaux d’interactions mutualistes favorise une structure imbriquée de ces derniers[1]. En effet, en raison du noyau de traits qui dirige la coévolution au sein du réseau, ce dernier s’organise autour d’un ensemble cohésif d’espèces généralistes qui interagissent les unes avec les autres et qui forment une ressource stable que les autres espèces peuvent exploiter, ce que font les spécialistes dont l’évolution est guidée par les interactions avec les généralistes. Cependant, les spécialistes sont rares car, plus le nombre d’espèces augmente, plus les alternatives évolutives à la spécialisation se font nombreuses. La sélection coévolutive favorise alors une asymétrie avec une grande abondance des généralistes[2].

Ainsi, deux forces de coévolution renforcent la structure imbriquée et asymétrique des réseaux d’interactions mutualistes: la complémentarité des traits mutualistes et la convergence entre des espèces non apparentées du fait de leurs interactions.

La stabilité d’un système écologique est sa capacité à retourner à son équilibre après une petite perturbation. Deux indices de stabilité fréquemment utilisés sont la persistance et la résilience.

La persistance correspond à la proportion d’espèces dans la communauté à son équilibre. La résilience est la vitesse à laquelle la communauté retourne à l’équilibre après une perturbation[5]. Il est également possible de parler de la robustesse d’un réseau, qui représente l’intensité de la perturbation qui entraînera la perte de 50% des espèces[19]. Un réseau robuste sera donc peu sensible aux perturbations, dans la mesure où celles-ci ne sont pas trop drastiques.

Figure 6. Résumé de l’influence des paramètres structuraux sur la stabilité. Les flèches oranges représentent un effet négatif. Les flèches bleues représentent un effet positif. L’épaisseur des flèches représente l’intensité de l’effet. Les lignes continues représentent les effets directs. Les lignes pointillées représentent les effets indirects.

Le modèle largement utilisé pour étudier la stabilité des réseaux d’interaction mutualistes est un modèle fréquence-dépendant dans lequel les bénéfices saturent avec la densité de partenaires.

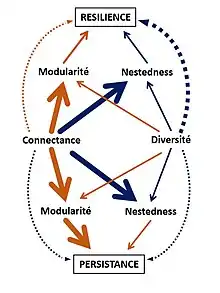
Les différents paramètres de la structure des réseaux jouent un rôle dans leur stabilité. La modularité et la nestedness influencent directement la persistance et la résilience des réseaux. La modularité a notamment un effet négatif sur la persistance, tandis que la nestedness favorise la résilience.

La connectance ainsi que la diversité ont des effets directs sur la stabilité du réseau ainsi que des effets indirects, par la modification de la modularité et de la nestedness. Les effets directs de la connectance et la diversité sur la persistance du réseau sont faibles par rapport aux effets indirects. On observe l’inverse pour la résilience.

Ainsi, une forte connectance et diversité diminuent la modularité et favorisent la nestedness, entraînant une augmentation de la persistance et la résilience[5].

La notion de force d'interaction joue elle aussi un rôle important dans la stabilité d’un système. Le retrait d’une espèce avec une forte connectance mais des interactions faibles aura un effet plus limité qu’une espèce avec la même connectance mais de fortes interactions.

Les informations sur la force des interactions doivent donc aussi être prises en compte dans les stratégies de conservation.

L’extinction d’une espèce peut en priver une autre d’une interaction qui lui serait vitale. Dans ce cas-là, la première extinction en entraîne une deuxième. Cet effet peut se produire à nouveau, ce qui amènerait à la perte de nombreuses espèces. Ce phénomène se nomme “cascade de coextinction”.

La structure hétérogène et imbriquée des réseaux d’interactions mutualistes les rend robustes face à la perte d’espèces. Dans ces réseaux, on retrouve des espèces avec peu de connexions différentes (spécialistes) et d’autres avec beaucoup (généralistes). La perte des espèces les plus spécialistes n’aura pas un grand effet sur la stabilité du réseau, et ne provoquera donc probablement pas de coextinction.

Figure 7. Représentation d’événements d’extinction au sein d’un réseau d’interactions mutualistes. Lorsqu’une espèce généraliste s’éteint, les espèces spécialistes qui en dépendaient s’éteignent à leur tour. Lorsqu’une espèce spécialiste s’éteint, cela n’impacte pas beaucoup la structure du réseau

A l’inverse, la perte d’espèces plus généralistes peut provoquer l'extinction d’espèces dépendantes à cette dernière, par leur spécialisation.

On en déduit donc qu’une extinction aléatoire d'espèces aurait peu d’effet car la majorité des espèces sont spécialistes. A l’inverse, l’extinction ciblée des espèces les plus généralistes pourrait entraîner de nombreuses extinctions à cause des cascades de coextinction[1].

À préciser que la phylogénie des espèces a également un impact sur les cascades de coextinction. En effet, les espèces les plus proches phylogénétiquement ont un rôle fonctionnel souvent similaire[1]. Cela va entraîner un effet de cascade plus fort pour les espèces proches dans l’arbre phylogénétique et donc augmenter l’effet des cascades de coextinction sur la perte de biodiversité taxonomique.

Dans le contexte actuel de changements globaux, des bouleversements affectent les interactions au sein des réseaux mutualistes. L’augmentation moyenne des températures et les différentes variabilités climatiques vont modifier la phénologie des plantes et des insectes. Ces modifications peuvent diminuer les possibilités  des interactions dans le temps, voire créer une incompatibilité entre deux espèces.

La modification du climat peut aussi changer la composition du réseau en provoquant la perte de certaines espèces et l'arrivée d’autres.