Quadrupôle électrostatique

En électrostatique, un quadrupôle est une distribution de charges telle que les barycentres des charges positives et des charges négatives soient confondus.

Quadrupôle électrique.

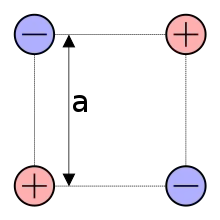
Analyse du quadrupôle

Soit une distribution $({\mathcal {D}})$ de charges $q_{i}$ aux points $P_{i}$ . Cette distribution $({\mathcal {D}})$ à support compact crée à une grande distance des charges (pour $r\gg a$ , avec $a$ longueur caractéristique de la distribution) un potentiel $V_{1}(r)$ .

On définit :

${\vec {r_{i}}}={\vec {OP_{i}}}$
$q=\sum _{i}q_{i}$ la somme des charges
${\vec {p}}(O)=\sum _{i}q_{i}{\vec {r_{i}}}$ , indépendant de $O$ si $q=0$ , nul si $O$ est choisi barycentre des charges
$J_{O}=\sum _{i}q_{i}r_{i}^{2}$ , le moment d'inertie par rapport à $O$
${\hat {J}}({\vec {X}})=\sum _{i}q_{i}{\vec {r_{i}}}\wedge ({\vec {X}}\wedge {\vec {r_{i}}})$ , l'opérateur linéaire d'inertie par rapport à $O$
${\hat {Q}}=2J_{o}X-3{\hat {J}}X$ , l'opérateur linéaire quadrupolaire en $O$

On peut vérifier que ${\hat {Q}}$ est de trace nulle : ${\textrm {Tr}}\ {\hat {Q}}=0$ .

Dans le cas d'une distribution continue de charge, l'expression de la composante $Q_{ij}$ du tenseur quadrupolaire est

$Q_{ij}=\int \rho \left(3r_{i}r_{j}-\|r\|^{2}\delta _{ij}\right){\textrm {d}}^{3}{\vec {r}}$ , où $\delta _{ij}$ est le symbole de Kronecker.

Développement quadrupolaire

Théorème :

$V_{1}({\vec {r}})={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{r}}+{\frac {{\vec {p}}\cdot {\vec {u}}}{r^{2}}}+{\frac {{\vec {u}}\cdot \left({\hat {Q}}{\vec {u}}\right)}{2r^{3}}}\right)+o\left({\frac {1}{r^{3}}}\right)$ , avec ${\vec {u}}={\frac {\vec {r}}{r}}$

En gravimétrie, ce théorème s'appelle formule de MacCullagh.

Cas particulier : axe de symétrie

Lorsque $({\mathcal {D}})$ possède une symétrie de révolution, les expressions du moment quadrupolaire se simplifient et ${\hat {Q}}$ est diagonale.

Si on suppose la symétrie autour de l'axe $(Oz)$ , alors la matrice des moments est $Q_{x,x}=Q_{y,y}=-Q_{o}/2$ et $Q_{z,z}=Q_{o}$ .

Si $q$ n'est pas nul, on choisit $O$ en $G$ , et alors :

$V_{1}({\vec {r}})={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{r}}+{\frac {Q_{o}}{2r^{3}}}\cdot P_{2}(cos\theta )\right)+o\left({\frac {1}{r^{3}}}\right)$ , avec $P_{2}(x)={\frac {3x^{2}-1}{2}}$ (3^e polynôme de Legendre).

Ce théorème vaut en gravimétrie pour la Terre supposée de révolution. Dans ce cas, $Q_{o}=2(A-C)$ < 0 ; l'usage est de poser $J_{2}={\frac {C-A}{Ma^{2}}}=1.08263\times 10^{-3}$ .

Le potentiel terrestre est ainsi $V(M)=-{\frac {GM}{r}}+{\frac {GMaJ_{2}P_{2}(cos\theta )}{r^{3}}}$ .

Ce développement peut être poussé plus loin (développement en harmoniques sphériques; termes en $J_{4}$ (octupolaire), $J_{6}$ , etc.).

Articles connexes

Cet article est issu de wikipedia. Texte licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.