Quadratrice d'Hippias
La quadratrice d’Hippias, trisectrice ou quadratrice de Dinostrate est une courbe mécanique dont l'invention est attribuée par Proclus au sophiste Hippias d'Élis (vers 420 av. J.-C.), qui s'en servit pour résoudre le problème de la trisection de l'angle (d'où son nom de « trisectrice »). Vers 350 av. J.-C., Dinostrate s'en servit pour résoudre la quadrature du cercle. C'est l'un des premiers exemples de courbe non-circulaire.
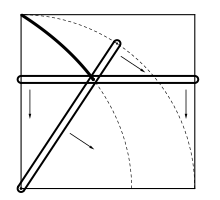
Définition
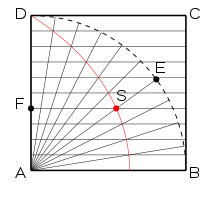
La quadratrice d'Hippias est décrite par composition d'un mouvement rectiligne uniforme avec un mouvement circulaire uniforme de la façon suivante. Dans le carré ABCD, on considère le quadrant DB de centre A. Soit E un point décrivant ce quart de cercle de D à B à vitesse constante, et soit F un point décrivant le segment DA à vitesse constante, de telle façon que E et F partent simultanément du point D et arrivent simultanément au point B (resp. A). La quadratrice est le lieu géométrique de l'intersection S du segment AE et de la parallèle à AB passant par F.
Si l'on note a le côté du carré et que l'on prend le point A comme origine d'un système de coordonnées cartésiennes avec l'axe des abscisses le long de AB, l'équation paramétrique de la quadratrice est
- ,
- .
On peut utiliser cette équation pour définir abstraitement la quadratrice, avec une difficulté liée cependant aux non-définitions de la fonction cot(t).
Application à la trisection de l'angle
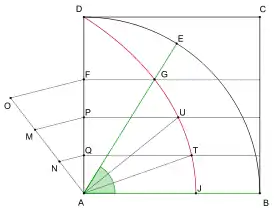
La trisection de l'angle est l'un des Trois grands problèmes de l'Antiquité, qui traduisent des cas d'inconstructibilité « à la règle et au compas ». Selon Proclus, Hippias aurait imaginé la quadratrice comme un moyen de diviser graphiquement un angle[1].
Par construction, l'angle au centre d'un point de la quadratrice est proportionnel à son ordonnée (comptée depuis D) ; par conséquent, si l'on peut découper un segment en parties égales, on divisera par là-même un angle en trois angles égaux. Or la division d'un segment en 3 segments égaux est constructible à la règle et au compas.
Soit ainsi l'angle BAE ( ≤ 90°) : on construit sur sa base AB un carré ABCD et l'on forme la quadratrice inscrite grâce au mécanisme décrit ci-dessus. L'autre côté de l'angle recoupe la quadratrice au point G, et la droite parallèle au côté AB issue de G intercepte le côté AD du carré au point F; le segment AF est proportionnel à l'arc BE ou, plus précisément, le rapport de longueurs AF/AD est égal au rapport des longueurs d'arcs BE/BD.
À présent, portons depuis A trois segments égaux alignés (AN, NM, MO) et traçons la droite OF ; puis menons depuis M et N des parallèles à cette droite ; on partage ainsi AF en trois segments égaux. Les parallèles à AB menées depuis les extrémités de ces segments : P, Q, coupent la quadratrice aux points U et T qui divisent exactement l'angle donné en trois angles égaux[2].
La quadratrice n'est pas constructible à la règle et au compas : ce n'est qu'une courbe « constructible par points », c'est-à-dire qu'on ne peut en construire qu'un ensemble dénombrable de points[3]. Il est vrai qu'on peut ainsi esquisser assez précisément la quadratrice, mais elle ne peut véritablement s'obtenir en totalité que par un mécanisme ; or il faut avoir toute la courbe pour pouvoir l'utiliser, car les points d'intersection utiles sont évidemment a priori indéterminés.
Application à la quadrature du cercle
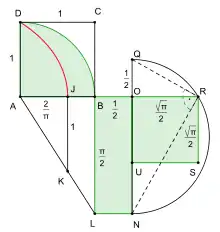
Comme la trisection de l'angle, la quadrature du cercle à la règle et au compas est impossible, mais la quadratrice d’Hippias permet la construction du carré cherché (ou, ce qui revient au même, d'un carré de même surface que le quart du cercle donné).
Le lemme de Dinostrate énonce[1] que la quadratrice d’Hippias divise le côté du carré dans le rapport . Autrement dit, étant donné un quadrant de rayon r, on forme d'abord le carré circonscrit ABCD (donc d'arête r). La quadratrice intercepte le côté AB du carré en J de telle sorte que .
La construction d'un carré de surface π/2 s'en déduit aisément.
Du point J, on élève un segment JK perpendiculaire à AB et de longueur r. Soit L le point d'intersection entre AK et le côté prolongé BC. D'après la similitude des triangles AJK et ABL, on a . Si à présent l'on prolonge le rayon AB d'un segment colinéaire , BL et BO forment les côtés d'un rectangle OBLN, dont la surface est celle du quart de cercle. Il reste à former un carré de même surface, ce qui s'obtient au moyen des relations métriques dans le triangle rectangle et du théorème de Thalès.
Pour cela, prolongeons ON d'un segment , décrivons un demi-cercle de diamètre NQ et prolongeons AO jusqu'à intercepter le demi-cercle. Soit R le point d'intersection. D'après le théorème de Thalès le triangle NQR est un triangle rectangle, et les relations métriques indiquent que sa hauteur OR est l'arête d'un carré de même surface que le rectangle OBLN.
Il importe de remarquer que le pantographe imaginé par Hippias ne permet pas d'obtenir le point d'intersection J de la quadratrice avec le côté AB du carré, car les deux réglettes (le rayon tournant et la réglette en translation verticale) se superposent lorsqu'elles passent par le point B, et donc n'ont plus d’intersection unique (réduite à un point). Et ainsi on ne peut pas davantage former le point J avec la quadratrice qu'avec la règle et le compas[4].
Historique
L'histoire de la quadratrice, sa construction et ses applications sont parvenues jusqu'à nous par trois sources différentes : Proclus (412-485), Pappus d'Alexandrie (IVe siècle) et Jamblique (vers 240-325). Proclus nomme Hippias comme l'inventeur de la quadratrice et montre comment Hippias a appliqué cette courbe à la trisection de l'angle. Pappus, pour sa part, montre comment Dinostrate, Nicomède et d'autres géomètres se sont servis d'une courbe qu'ils appelaient « quadratrice » pour résoudre graphiquement le problème de la quadrature du cercle ; nulle part il ne fait allusion à Hippias, et n'évoque pas même son nom avec celui de la courbe. Jamblique indique seulement au détour d'une phrase que Nicomède s'est servi d'une courbe quadratrice pour quarrer le cercle[5]. Bien que son nom de quadratrice, donné par Proclus, donne à penser qu'Hippias l'a imaginée pour résoudre le problème de la quadrature, Moritz Cantor, et à sa suite Thomas Heath[5] et Abel Rey[1], s'ils admettent que c'est bien Hippias qui l'a inventée, estiment en revanche qu'il ne l'a fait qu'en vue de résoudre la trisection de l'angle, et que son application à la quadrature est l'œuvre de géomètres postérieurs, vraisemblablement Dinostrate et Nicomède.
Voir aussi
Article connexe
La cissoïde de Dioclès, un mésolabe.
Bibliographie
- Henri Lebesgue, Leçons sur les constructions géométriques, Paris, Gauthier-Villars, (réimpr. 2003), 318 p., « 1-La solution des problèmes fondamentaux : trisection de l'angle, duplication du cube »
- Robert Baccou, Histoire de la science grecque, de Thalès à Socrate, Paris, Aubier, , 256 p.
- Felix Klein, Famous Problems of Elementary Geometry, Boston etc., Ginn & Co., (réimpr. 2007) (lire en ligne), p. 57-58)
- Thomas Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, Clarendon Press, (réimpr. Elibron Classics 2006), p. 225-230.
Liens externes
- La quadratrice de Dinostrate sur MathCurve.
- La quadratrice et la quadrature du cercle sur le site de l’université de Lunebourg.
- Michael D. Huberty, Ko Hayashi, Chia Vang: La quadratrice d'Hippias.
- (en) Quadratrix of Hippias sur le site MathWorld.
Références
- Abel Rey, L'Apogée de la science technique grecque, vol. IV : Les mathématiques d'Hippocrate à Platon, Albin Michel, coll. « L’Évolution de l'Humanité », , chap. 5 (« De la quadrature à la trisection de l'angle et à la géométrie supérieure : Hippias d'Élée »), p. 224-227.
- D'après (en) Underwood Dudley, The Trisectors, Washington (D.C.), CUP, , 184 p. (ISBN 0-88385-514-3, lire en ligne), p. 6-8.
- Cf. Lebesgue 1950, partie III, no 1, « Courbes constructibles par points quelconques ».
- Cf. Jean-Paul Delahaye, Le Fascinant Nombre π [détail de l’édition], chap. 3 (« Histoire de π au temps de la géométrie »), p. 54.
- (en) Thomas Little Heath, A History of Greek Mathematics, vol. 1 : From Thales to Euclid, CUP, (1re éd. 1921) (ISBN 978-1-108-06306-7, lire en ligne).
![{\displaystyle \gamma :[0,{\tfrac {\pi }{2}}]\rightarrow \mathbb {R} ^{2}}](https://img.franco.wiki/i/ccbaddd1f18c766e4a16c50a0c177ee3678c6803.svg)





