Procédé en cascade
En génie chimique, un procédé en cascade est une technique se déployant en plusieurs étages d'opérations unitaires identiques, chaque étage opérant sur le produit de l'étage précédent. On trouve des procédés en cascade dans la séparation isotopique, la distillation, la flottation, et divers autres procédés de séparation ou de purification.
Les procédés en cascade se rencontrent le plus souvent pour enrichir un mélange hétérogène : il est alors question d'une cascade d'enrichissement.
Quand la performance d'un étage ne varie guère suivant la concentration générale, ce qui est le plus souvent le cas, la mise en cascade permet d'augmenter exponentiellement l'efficacité du procédé. Ainsi, pour distiller de l'eau, si une distillation enlève 99 % des impuretés, l'eau bi-distillée sera pure à 99,99 %, et trois distillations ne laisseront que (1-99 %)3 soit 1 ppm des impuretés d'origine.
Procédés en cascade
On rencontre des procédés en cascade à chaque fois qu'un étage serait insuffisant ou inefficient pour obtenir le résultat visé. Par exemple, dans de nombreux procédés d'enrichissement isotopique de l'uranium, l'isotope recherché (uranium 235) n'est que très faiblement enrichi par le passage dans une étape de traitement. Pour obtenir un enrichissement significatif, de nombreuses étapes doivent être enchaînées, parfois plusieurs centaines, chaque étage alimentant l'étage suivant par un mélange légèrement plus riche que celui qu'il reçoit.
On rencontre des mises en cascade dans d'autres domaines :
- en physique, un autre exemple est celui de la liquéfaction de l'air, basée sur le refroidissement consécutif à une détente adiabatique. Pris isolément, un compresseur ne peut pas liquéfier de l'air à température ambiante ; mais la mise en cascade des flux thermiques entre compresseurs permet d'extraire en fin de compte suffisamment d'énergie pour obtenir l'air à l'état liquide ;
- une fusée à étages correspond à la mise en cascade de trois fusées élémentaires ;
- dans le domaine financier, on peut rencontrer un phénomène similaire dans les achats à effet de levier.
Cependant, seuls les enrichissement de mélanges ou de distillation soulèvent des questions de calcul d'étages complexes, qui seront décrits dans la suite de l'article.
Performance d'une cascade
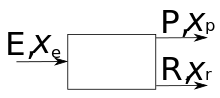
Notations
Une unité élémentaire à l'étage i réalise la séparation d'une masse en entrée en entrée, de teneur , en une masse produit de produit de sortie de teneur , et un résidu de masse ayant comme teneur[1]. Dans une cascade idéale, le point de fonctionnement de cette unité élémentaire doit être choisi au voisinage de son point de fonctionnement optimal, si bien que toutes les unités doivent fonctionner avec des valeurs sensiblement identiques. Ceci impose que le nombre d'unités varie d'un étage à l'autre ; dans le cas contraire d'une cascade carrée (par exemple, une colonne de distillation) le travail varie d'un étage à l'autre.
Le travail de séparation correspondant à cette opération élémentaire est exprimé par :
Avec :
- .
Le facteur de séparation associé à cet étage est la variation relative des richesses de concentration du produit à concentrer, entre l'entrée et la sortie :
On peut montrer que le facteur de séparation ainsi défini ne dépend pas des concentrations, et qu'il est une propriété caractéristique du procédé. En revanche, il peut dépendre fortement du débit d'entrée et du fractionnement P/E.
Couplage des étages
.jpg.webp)
Dans une cascade d'enrichissement, chaque étage est alimenté par le produit de l'étage inférieur. De proche en proche, le flux produit devient donc de plus en plus concentré.
Le flux rejeté par un étage élémentaire doit généralement être recyclé, d'une part pour ne pas dilapider la matière correspondante, d'autre part pour ne pas perdre le travail de séparation que représente leur concentration partielle. Le montage le plus simple est celui d'une cascade symétrique, où le résidu de chaque étage est mélangé au flux entrant de l'étage inférieur. Pour que ce mélange se fasse sans perte de travail de séparation, il faut que les concentrations et soient égales. Dans ce cas, on montre également que le coefficient de partage doit être égal à 1/2. D'autres montages sont possibles si le rapport entre et s'éloigne trop de l'unité : si par exemple l'étage élémentaire est optimisé de telle manière que est de l'ordre de grandeur de , un montage asymétrique transférera le flux appauvri deux étages plus bas dans la cascade. Les montages correspondants sont évidemment plus complexes, mais ne changent pas le principe de fonctionnement d'une cascade.
En général, l'enrichissement obtenu par un étage élémentaire est relativement faible :
- avec
Dans ce cas, le facteur de séparation α d'un étage (caractéristique du procédé, et ne dépendant que du débit et du coefficient de partage, mais non des concentrations) peut s'exprimer en fonction de ce gain élémentaire :
- ou encore
Sous cette dernière forme, on voit que le rapport des teneurs entre entrée et sortie d'un étage est sensiblement constant tant que ces teneurs restent petites, et est égal au facteur de séparation de l'étage élémentaire. Inversement, lorsque ces concentrations deviennent significatives, le gain sur les teneurs devient progressivement plus faible, et tend évidemment à s'annuler quand la teneur s'approche de 100 %.
Le fonctionnement des unités élémentaires étant supposé identique d'un étage à l'autre, on voit que le coût d'enrichissement est d'autant plus élevé que la concentration du produit est forte ; c'est-à-dire inversement que dans une cascade même idéale, à quantité de travail égale, le gain en concentration devient progressivement d'autant plus faible que la concentration est forte. C'est le passage à la limite de cette équation, avec tendant vers zéro pour des étages « infiniment minces », qui conduit à l'équation différentielle de l'unité de travail de séparation, proposée par Paul Dirac dans les années 1940.
L'approximation α=cte peut néanmoins servir pour déterminer approximativement le nombre d'étages n nécessaires pour obtenir l'enrichissement Q, qui sera au minimum :
Par exemple, pour enrichir de l'uranium naturel à 0,71 % jusqu'à une teneur de 3,5 % par un procédé dont le facteur de séparation est de 1,0833, il sera nécessaire d'enchaîner au moins Log(4,93)/Log(1,0833)= 20 étages d'enrichissement au moins.
Section d'épuisement
La répartition entre les flux de sortie se calcule simplement en fonction des concentrations en écrivant que le flux total de matière et le flux de composé sont simultanément conservés :
d'où l'on déduit facilement que le rapport entre masse de produit et masse d'entrée (le coefficient de partage θ) est donné par l'expression :
Cette expression traduit le fait (intuitivement évident) que plus on épuise le mélange traité, moins on a besoin d'en fournir en entrée pour obtenir une quantité enrichie donnée ; ou inversement, plus le déchet contient encore de l'isotope recherché non séparé, et plus l'alimentation du processus doit être importante, pour en sortie obtenir la production désirée. Autrement dit, si les teneurs d'alimentation xe et de production xp sont imposées, pour une production donnée, le flux d'alimentation nécessaire diminue avec xr.
De ce fait, un procédé en cascade ne se limite pas à une section d'enrichissement, mais comporte également une section d'épuisement. L'importance de cette section d'épuisement est déterminée par des considérations économiques : ce que l'on gagne en matière première économisée se traduit par un coût d'investissement en unités d'enrichissement, et un coût de production des unités de travail de séparation. De cet arbitrage on peut déduire la concentration xr optimale, celle où le gain marginal d'un étage d'épuisement supplémentaire est équilibré par le produit qu'elle permet d'économiser.
Notes et références
Notes
- Les publications anglaises utilisent traditionnellement les indices f, p, et w ou t, pour feed, product, et waste ou parfois tail.
Références
- Daniel Massignon, « Enrichissement de l'uranium », Éditions techniques de l'ingénieur, traité Génie nucléaire





















