Pression de vapeur saturante de l'eau
La pression de vapeur saturante de l'eau est la pression à laquelle la vapeur d'eau est en équilibre thermodynamique avec son état condensé. Lorsque la pression partielle de la vapeur d'eau devient plus grande, celle-ci est supposée se condenser.
Formules
Sauf indication contraire, les températures notées sont exprimées en kelvins (K), les températures notées en degrés Celsius (°C), les pressions en pascals (Pa).
Rankine
La formule de Rankine est obtenue par intégration de la formule de Clausius-Clapeyron, valable pour les gaz parfaits, en considérant l'enthalpie de vaporisation constante[1] - [2] :
- ,
où = 18,01 × 10−3 kg mol−1 kg/mol est la masse molaire de l'eau, = 8,314 462 618 153 24 J mol−1 K−1 est la constante universelle des gaz parfaits, est la température considérée (K). Les bornes d'intégration et sont choisies pour un point d'ébullition connu. À pression atmosphérique normale = 1 atm = 1 013,25 hPa, = 100 °C = 373,15 K ; de plus on choisissant = 2,365 × 106 J kg−1, on obtient la formule de Rankine[3] - [4], qui peut être considérée comme une simplification de la formule de Dupré[5] :
- .
Antoine
Il s'agit d'une amélioration de la formule de Rankine pour s'approcher davantage de données expérimentales :
- ,
- en kelvins, en bars.
| Coefficient | Coefficient | Coefficient | Température (K) | Référence |
|---|---|---|---|---|
| 4,65430 | 1 435,264 | −64,848 | 255,9 - 373 | [7] |
| 5,40221 | 1 838,675 | −31,737 | 273 - 303 | [8] |
| 5,20389 | 1 733,926 | −39,485 | 304 - 333 | [8] |
| 5,07680 | 1 659,793 | −45,854 | 334 - 363 | [8] |
| 5,08354 | 1 663,125 | −45,662 | 344 - 373 | [8] |
| 3,55959 | 643,748 | −198,043 | 379 - 573 | [9] |
ISO 13788
Une relation simple est proposée dans la norme NF EN ISO 13788:2012[10] :
- .
Avec la température en degrés celsius.
Sonntag ; NF X15-110
Plusieurs formules sont proposées par A. Wexler et corrigées par D. Sonntag[11] - [12], selon qu'il s'agisse de vapeur au contact de l'eau ou de la glace. Elles sont citées dans la norme NF X15-110[13]. Des facteurs d'augmentation sont proposés afin de connaitre la pression de vapeur saturante pour l'air humide.
Pression de vapeur saturante en phase pure au-dessus d'une surface d'eau :
- ,
- pour
Pression de vapeur saturante en phase pure au-dessus d'une surface de glace :
- ,
- pour .
Facteurs d'augmentation :
- ,
- .
Si le facteur d'augmentation a peu d'importance dans les conditions de pression et de température ordinaires, il doit être pris en compte pour de fortes pressions. Il permet de tenir compte de l'effet des gaz dissouts dans le condensat ou encore l'effet des forces intermoléculaires sur les propriétés des fluides[13].
Hardy
Plusieurs formules sont proposées par Bob Hardy[14]. Comme précédemment elles prévoient l'équilibre eau-vapeur et glace-vapeur ainsi que les facteurs d'augmentation utiles pour évaluer les pressions de vapeur saturante dans le cas de l'air humide.
Pression de vapeur saturante en phase pure au-dessus d'une surface d'eau :
- pour .
Pression de vapeur saturante en phase pure au-dessus d'une surface de glace :
- pour .
Facteurs d'augmentation en présence d'autres gaz :
- avec et , étant la température en degrés celsius.
| Eau
|
Eau
|
Glace
| |
|---|---|---|---|
| 3,621 83.10-4 | 3,53624.10-4 | 3.64449.10-4 | |
| 2,606 124 4.10-5 | 2,9328363.10-5 | 2.9367585.10-5 | |
| 3,866 777 0.10-7 | 2,6168979.10-7 | 4.8874766.10-7 | |
| 3,826 895 8.10-9 | 8,5813609.10-9 | 4.3669918.10-9 | |
| -1,076 04.101 | -1,07588.101 | -1.07271.101 | |
| 6,398 744 1.10-2 | 6,3268134.10-2 | 7.6215115.10-2 | |
| -2,635 156 6.10-4 | -2,5368934.10-4 | -1.7490155.10-4 | |
| 1,672 508 4.10-6 | 6,3405286.10-7 | 2.4668279.10-6 |
Tables
Le tableau suivant rassemble, pour différentes formulations, la pression de vapeur saturante en phase pure au contact de l'eau, et la pression de valeur saturante de l'air humide .
| T(K) | θ(°C) | Psat (Pa) | P'sat (Pa) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rankine | Antoine | Sonntag NF EN ISO 13788 | NF X15-110 | Hardy | Wagner et Pruß IAPWS | NF X15-110 | Hardy | ||
| 273,15 | 0 | 653,312 | 610,809 | 610,500 | 611,213 | 611,213 | 611,213 | 613,906 | 613,574 |
| 283,15 | 10 | 1 266,543 | 1 227,002 | 1 227,310 | 1 228,133 | 1 228,139 | 1 228,112 | 1 233,526 | 1 232,884 |
| 293,15 | 20 | 2 346,954 | 2 336,727 | 2 336,951 | 2 339,249 | 2 339,262 | 2 339,194 | 2 349,783 | 2 348,600 |
| 303,15 | 30 | 4 175,571 | 4 243,806 | 4 240,505 | 4 247,029 | 4 247,046 | 4 246,920 | 4 267,206 | 4 265,156 |
| 313,15 | 40 | 7 160,558 | 7 378,132 | 7 370,928 | 7 385,296 | 7 385,299 | 7 385,110 | 7 423,157 | 7 419,875 |
| 323,15 | 50 | 11 876,297 | 12 339,754 | 12 328,554 | 12 352,743 | 12 352,690 | 12 352,479 | 12 421,821 | 12 417,018 |
| 333,15 | 60 | 19 108,385 | 19 927,585 | 19 919,308 | 19 947,664 | 19 947,476 | 19 947,383 | 20 068,340 | 20 061,902 |
| 343,15 | 70 | 29 903,969 | 31 177,088 | 31 194,319 | 31 202,327 | 31 201,894 | 31 202,199 | 31 398,686 | 31 390,516 |
| 353,15 | 80 | 45 626,617 | 47 371,365 | 47 489,554 | 47 415,543 | 47 414,751 | 47 415,784 | 47 696,546 | 47 686,137 |
| 363,15 | 90 | 68 014,618 | 70 104,267 | 70 464,025 | 70 182,213 | 70 181,042 | 70 182,678 | 70 479,428 | 70 467,036 |
| 373,15 | 100 | 99 241,488 | 101 291,009 | 102 135,228 | 101 419,042 | 101 417,770 | 101 417,994 | 101 417,859 | 101 416,668 |
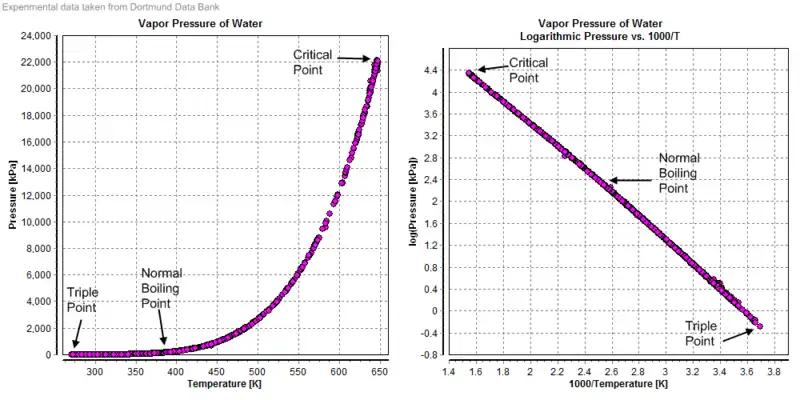
Graphes donnant la pression de vapeur saturante de l'eau en fonction de la température
Références
- Collectif, Tout le Cours - Thermodynamique - PCSI MPSI PTSI, NATHAN (ISBN 978-2-09-812153-9, lire en ligne).
- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, De Boeck Superieur, (ISBN 978-2-8073-0744-5, lire en ligne), p. 236.
- Vidal Lionel, Régis Bourdin, Ludovic Menguy, Vincent Parmentier, Jean Lou Reynier, Nicolas Ta, Physique PT/PT* - 3e édition actualisée, Editions Ellipses, (ISBN 978-2-340-04178-3, lire en ligne), p. 482.
- Pascal Febvre, Richard Taillet et Loïc Villain, Dictionnaire de physique, De Boeck Superieur, (ISBN 978-2-8041-7554-2, lire en ligne), p. 575.
- Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, De Boeck Superieur, (ISBN 978-2-8073-0744-5, lire en ligne).
- (en) « Water », sur NIST/WebBook (consulté le 21 juin 2010).
- Daniel R. Stull, « Vapor Pressure of Pure Substances. Organic and Inorganic Compounds », Industrial & Engineering Chemistry, vol. 39, no 4, , p. 517–540 (ISSN 0019-7866, DOI 10.1021/ie50448a022, lire en ligne, consulté le ).
- O. C. Bridgeman et E. W. Aldrich, « Vapor Pressure Tables for Water », Journal of Heat Transfer, vol. 86, no 2, , p. 279–286 (ISSN 0022-1481, DOI 10.1115/1.3687121, lire en ligne, consulté le ).
- Chia-Tsun Liu et William T. Lindsay, « Vapor pressure of deuterated water from 106 to 300.deg. », Journal of Chemical & Engineering Data, vol. 15, no 4, , p. 510–513 (ISSN 0021-9568, DOI 10.1021/je60047a015, lire en ligne, consulté le ).
- « NF EN ISO 13788 : Performance hygrothermique des composants et parois de bâtiments - Température superficielle intérieure permettant d'éviter l'humidité superficielle critique et la condensation dans la masse - Méthodes de calcul », sur Afnor EDITIONS (consulté le ).
- (en) D. Sonntag, « Important new values of the physical constants of 1986, vapour pressure formulations based on the ITS-90, and psychrometer formulae. », Zeitschrift fuer Meteorologie, , p. 340-344.
- Bernard Crétinon et Bertrand Blanquart, « Air humide : Notions de base et mesures », Techniques de l'ingénieur, , p. 4 (lire en ligne
 ).
). - « NF X15-110 : Mesure de l'humidité de l'air - Paramètres hygrométriques », sur Afnor EDITIONS (consulté le ).
- (en) Bob Hardy, « ITS-90 formulations for vapor pressure, frostpoint temperature, dewpoint temperature, and enhancement factors in the range –100 TO +100 °C », The Proceedings of the Third International Symposium on Humidity & Moisture, (lire en ligne).
- (en) W. Wagner et A. Pruß, « The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use », Journal of Physical and Chemical Reference Data, , p. 387-535.
Annexes
Articles connexes
- Formule de Duperray
- Formule de Dupré
- Équation de Goff-Gratch (en)
Bibliographie
- (en) Garnett, Pat ; Anderton, John D ; Garnett, Pamela J, Chemistry Laboratory Manual For Senior Secondary School, Longman, (ISBN 0-582-86764-9).
- (en) Murphy, D. M. et Koop, T., « Review of the vapour pressures of ice and supercooled water for atmospheric applications », Quarterly Journal of the Royal Meteorological Society, vol. 131, no 608, , p. 1539–1565. (DOI 10.1256/qj.04.94).
Liens externes
(en) Holger Vömel, Différentes équations pour la pression de vapeur saturante, CIRES, université du Colorado, Boulder




![{\displaystyle P_{\mathrm {sat} }=P_{0}\times \exp \!\left[{\Delta _{\text{vap}}H\times M \over R}\left({1 \over T_{0}}-{1 \over T}\right)\right]}](https://img.franco.wiki/i/64cefb266604af6d18cc6d6b0d0fba687195c0f1.svg)
















![{\displaystyle f_{w}={\frac {P'_{w{\text{ sat}}}}{P_{w{\text{ sat}}}}}=1+{\frac {10^{-6}\,P_{w{\text{ sat}}}(\theta )}{273+\theta }}\left[\left(38+173\,e^{\theta /43}\right)\left(1-{\frac {P_{w{\text{ sat}}}(\theta )}{P}}\right)+\left(6{,}39+4{,}28\,e^{-\theta /107}\right)\left({\frac {P}{P_{w{\text{ sat}}}(\theta )}}-1\right)\right]}](https://img.franco.wiki/i/874ca305f4ddf2c0b75c0a665f35b03b606af7fa.svg)
![{\displaystyle f_{i}={\frac {P'_{i\ \mathrm {sat} }}{P_{i\ \mathrm {sat} }}}=1+{\frac {10^{-7}\,P_{i\ \mathrm {sat} }(\theta )}{273+\theta }}\left[\left(2100-65\,\theta \right)\left(1-{\frac {P_{i\ \mathrm {sat} }(\theta )}{P}}\right)+\left(109-0{,}35\,\theta +{\frac {\theta ^{2}}{338}}\right)\left({\frac {P}{P_{i\ \mathrm {sat} }(\theta )}}-1\right)\right]}](https://img.franco.wiki/i/33aa6e5d5a2cd32b8512215b5790a86c1e138167.svg)


![{\displaystyle f={\frac {P'_{\text{sat}}}{P_{\text{sat}}}}=\exp \left[\alpha \left(1-{\frac {P_{\text{sat}}(T)}{P}}\right)+\beta \left({\frac {P}{P_{\text{sat}}(T)}}-1\right)\right]}](https://img.franco.wiki/i/c369a5c06a96543627ab8c41f8b2754425076770.svg)















