Porte de Toffoli

En informatique, la porte de Toffoli, est une porte logique. Elle est réversible et universelle, ce qui signifie que n'importe quel circuit réversible peut être construit à partir de portes de Toffoli. Elle agit comme une porte NON à double contrôle, d'où le nom qu'on lui donne également de « controlled-controlled-not gate » (CCNOT).

Elle est due à Tommaso Toffoli.

Définition

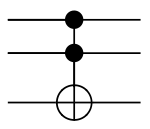
Représentation d'une porte de Toffoli

La porte de Toffoli est une porte logique à 3 bits en entrée et 3 bits en sortie. Si les deux premiers bits sont égaux à 1, le troisième bit est inversé, comme le montrent les représentations suivantes :

Table de vérité

Matrice de permutation

ENTRÉE			SORTIE
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	0	1
1	1	0	1	1	1
1	1	1	1	1	0

$\left[\ {\begin{matrix}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&1&0\\\end{matrix}}\ \right]$

Autrement dit, pour trois bits en entrée a, b, et c nous obtenons en sortie a, b, et (c XOR (a ET b)).

Réversibilité

Définition

Une porte logique L est réversible si, pour toute sortie y, il existe une entrée x unique telle que L(x) = y. Si une porte L est réversible, il existe une porte inverse L’ pour laquelle L’(y) = x. Par exemple, la porte NON est réversible, comme le montre sa table de vérité :

ENTRÉE	SORTIE
0	1
1	0

Par contre, la porte ET n'est pas réversible, les entrées 00, 01 et 10 ayant toutes trois pour sortie 0.

Importance

On s'est intéressé aux portes logiques réversibles dans les années 1960, parce que les portes réversibles dissipent moins de chaleur que les autres (en principe elles pourraient même à la limite n'en dissiper aucune). Dans une porte classique, les états d'entrée ne sont pas systématiquement conservés et nous obtenons généralement moins d'information en sortie qu'en entrée. Cette perte entraîne aussi une perte d'énergie, sous forme de chaleur, selon le principe de l'entropie en thermodynamique. Autrement dit, il faut de l'énergie pour permettre la transformation des bits d'information. Une porte réversible ne fait que modifier l'état des bits sans perte d'information, l'énergie est donc conservée[1].

Plus récemment, l'intérêt est venu de l'informatique quantique[2]. La physique quantique impose l'utilisation de transformations réversibles, mais permet en contrepartie de travailler avec des états plus larges pour réaliser des calculs à l'aide du principe de superposition. Les portes réversibles forment un sous-ensemble des portes autorisées par l'informatique quantique.

Universalité et porte de Toffoli

Selon le principe des tiroirs, toute porte réversible doit avoir le même nombre de bits en entrée et en sortie.

Pour un seul bit d'entrée, il existe deux portes réversibles. La première est la porte NON qui inverse 0 et 1, et la seconde la porte d'identité qui n'entraîne aucun changement.
Pour deux bits d'entrée, il n'existe qu'une seule porte non triviale la porte CNOT (en), qui, étant donné deux bits d'entrée, restitue le premier et donne comme second le OU exclusif des deux entrées :

Table de vérité

Matrice de permutation

INPUT		OUTPUT
0	0	0	0
0	1	0	1
1	0	1	1
1	1	1	0

$\left[\ {\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\\\end{matrix}}\ \right]$

Malheureusement, il existe des fonctions réversibles qui ne peuvent pas être réalisées en utilisant seulement ces portes. Autrement dit, le jeu de portes composé de NON et de XOR n'est pas universel (voir l'intégralité fonctionnelle). Si nous tenons à réaliser une fonction quelconque à l'aide de portes réversibles, nous avons besoin d'une autre porte. La porte de Toffoli, proposée en 1980 par Tommaso Toffoli, est une solution[3] - [4].

La porte de Toffoli est universelle, ce qui signifie que, quelle que soit la fonction booléenne f(x₁, x₂, ..., x_m), il y a un circuit composé de portes de Toffoli qui

prend en entrée x₁, x₂, ..., x_m — plus quelques bits supplémentaires à 0 ou à 1 ;
a comme sortie x₁, x₂, ..., x_m, f(x₁, x₂, ..., x_m) — plus quelques autres bits, inutilisés.

On peut donc construire avec des portes de Toffoli des systèmes qui réaliseront de façon réversible une fonction booléenne quelconque.

Liens avec l'informatique quantique

Toute porte réversible peut être implantée sur un ordinateur quantique. La porte de Toffoli est donc aussi un opérateur quantique. Mais elle n'est pas un opérateur quantique universel, même s'il est vrai que l'ordinateur quantique peut réaliser tous les calculs classiques.

Une porte de Toffoli a été réalisée en janvier 2009 à l'université d'Innsbruck en Autriche[5].

Portes semblables

Représentation Fredkin–Toffoli des portes sous forme de boules de billard

La porte de Fredkin (en) est une porte réversible à trois bits qui permute les deux derniers bits si le premier est à 1 (permutation contrôlée)[6].
La porte de Toffoli à n bits est une généralisation de la porte de Toffoli. Elle a n bits en entrée (x₁, x₂, ..., x_n) et n bits en sortie. Les n−1 premiers bits sortent inchangés ; le dernier est (x₁ ET ... ET x_n−1) XOR x_n.
On peut construire une porte de Toffoli avec cinq portes quantiques à 2 qubits[7].
Cette porte est l'une des portes réversibles modélisables par boules de billard[8]. Cette modélisation est due à Fredkin et Toffoli[4].

Références

Voir le principe auquel Rolf Landauer a donné son nom.
(Barenco et al. 1982)
(Toffoli 1980)
(Fredkin et Toffoli 1982)
(Monz et al.)
Porte de Fredkin quantique
(Barenco et al. 1995)
Voir en:Billiard-ball computer dans la Wikipédia en anglais.

Bibliographie

(en) T. Monz, K. Kim, W. Hänsel, M. Riebe, A. S. Villar, P. Schindler, M. Chwalla, M. Hennrich et R. Blatt, « Realization of the quantum Toffoli gate with trapped ions », Physical review letters, American Physical Society, vol. 102, n^o 4,‎ 2009 (DOI 10.1103/PhysRevLett.102.040501, arXiv 0804.0082)
(en) Adriano Barenco, Charles H. Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin et Harald Weinfurter, « Elementary gates for quantum computation », Phys. Rev. A, vol. 52,‎ mars 1982, p. 3457–3467 (DOI 10.1103/PhysRevA.52.3457, lire en ligne)
Tommaso Toffoli, « Reversible computing », dans Automata, Languages and Programming, Seventh Colloquium, Noordwijkerhout, Netherlands, J. W. de Bakker et J. van Leeuwen, 1980 (ISBN 3 540 10003 2, lire en ligne [archive du 15 avril 2010]), p. 632-644
(en) Edward Fredkin et Tommaso Toffoli, « Conservative logic », International Journal of Theoretical Physics, Springer Netherlands, vol. 21, n^o 3,‎ 1982, p. 219–253 (ISSN 0020-7748, DOI 10.1007/BF01857727, lire en ligne [archive du 11 mars 2012])
(en) Adriano Barenco, Charles H. Bennett, Cleve Richard, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin et Harald Weinfurter, « Elementary gates for quantum computation », Phys. Rev. A, American Physical Society, vol. 52, n^o 5,‎ 1995, p. 3457–3467 (PMID 9912645, DOI 10.1103/PhysRevA.52.3457, Bibcode 1995PhRvA..52.3457B, arXiv quant-ph/9503016)

Voir aussi

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.