PolynĂŽme de Touchard
Les polynÎmes de Touchard, étudié par Jacques Touchard[1], aussi appelés polynÎmes exponentiels[2] - [3] - [4] ou polynÎmes de Bell[5], constituent une suite de polynÎmes de type polynomial[6] définie par
- ,
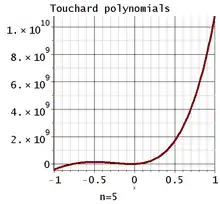
5Ăšme polynĂŽme de Touchard
oĂč est le nombre de Stirling de seconde espĂšce qui compte le nombre de partitions d'un ensemble de Ă©lĂ©ments en sous-ensembles non vides disjoints.
Propriétés
- La valeur en 1 du -iĂšme polynĂŽme de Touchard est le -iĂšme nombre de Bell, c'est-Ă -dire le nombre de partitions d'un ensemble de taille :
- .
- Les polynÎmes de Touchard vérifient
- .
- La suite de polynÎmes est de type binomial, et satisfait les identités
- .
- Les polynÎmes de Touchard sont la seule suite polynomiale de type binomial dont le coefficient du terme de degré 1 est égal à 1 dans chaque polynÎme.
- Les polynÎmes de Touchard vérifient une formule de Rodrigues :
- Les polynÎmes de Touchard vérifient les relations de récurrence :
- et .
- Pour , elle se réduit à la formule de récurrence pour les nombres de Bell.
- Avec la notation empruntée au calcul ombral, ces formules deviennent :
- et
- La série génératrice des polynÎmes de Touchard est :
- ,
- ce qui correspond à la série génératrice des nombres de Stirling de seconde espÚce.
- Les polynÎmes de Touchard admettent une représentation par intégrale de contour :
- .
ZĂ©ros
Les zéros des polynÎmes de Touchard sont réels négatifs[7]. Le plus petit zéro est minoré, en valeur absolue, par[8] :
et il est conjecturé que le plus petit zéro croßt linéairement avec l'index n.
On peut encadrer la mesure de Mahler des polynĂŽmes de Touchard comme suit[9] :
oĂč et sont les plus petits indices k qui maximisent respectivement et .
Généralisations
- Les polynĂŽmes de Bell complets peuvent ĂȘtre vus comme une gĂ©nĂ©ralisation multivariĂ©e des polynĂŽmes de Touchard , puisque
- .
- Les polynĂŽmes de Touchard (et par consĂ©quent aussi les nombres de Bell) peuvent ĂȘtre gĂ©nĂ©ralisĂ©s Ă des indices fractionnaires en utilisant la partie rĂ©elle de lâintĂ©grale donnĂ©e plus haut :
- .
Références
- (en) Cet article est partiellement ou en totalitĂ© issu de lâarticle de WikipĂ©dia en anglais intitulĂ© « Touchard polynomials » (voir la liste des auteurs).
- Jacques Touchard, « Sur les cycles des substitutions », Acta Mathematica, vol. 70, no 1,â?/span> , p. 243â?97 (ISSN 0001-5962, DOI 10.1007/BF02547349, MR 1555449).
- Steven Roman, The Umbral Calculus, Dover, , 193 p. (ISBN 0-486-44139-3).
- Khristo N. Boyadzhiev, « Exponential polynomials, Stirling numbers, and evaluation of some gamma integrals », Abstract and Applied Analysis, vol. 2009,â?/span> , p. 1â?8 (DOI 10.1155/2009/168672, Bibcode 2009AbApA2009....1B, arXiv 0909.0979).
- Bruce C. Brendt, « Ramanujan reaches his hand from his grave to snatch your theorems from you », Asia Pacific Mathematics Newsletter, vol. 1, no 2,â?/span> , p. 8-13 (lire en ligne, consultĂ© le ).
- (en) Eric W. Weisstein, « Bell Polynomial », sur MathWorld.
- Une suite de polynĂŽmes indexĂ©s par { 0, 1, 2, 3, ... }, oĂč l'index de chaque polynĂŽme est Ă©gal Ă son degrĂ©, est de type polynomial si elle vĂ©rifie les identitĂ©s
- .
- Lawrence H. Harper, « Stirling behavior is asymptotically normal », The Annals of Mathematical Statistics, vol. 38, no 2,â?/span> , p. 410â?14 (DOI 10.1214/aoms/1177698956)
- IstvĂĄn MezĆ et Roberto B. Corcino, « The estimation of the zeros of the Bell and r-Bell polynomials », Applied Mathematics and Computation, vol. 250,â?/span> , p. 727â?32 (DOI 10.1016/j.amc.2014.10.058).
- IstvĂĄn MezĆ, « On the Mahler measure of the Bell polynomials » (consultĂ© le ).
Articles liés
Cet article est issu de wikipedia. Texte licence: CC BY-SA 4.0, Des conditions supplĂ©mentaires peuvent sâappliquer aux fichiers multimĂ©dias.



























