Polynôme d'Ehrhart

L'idée de la construction de Ehrhart est de considérer comme fonction de t le nombre de points entiers intérieurs à un polytope obtenu par homothétie par un facteur t du polytope étudié.

Plus précisément, soit un réseau ${\displaystyle {\mathcal {L}}}$ de l'espace euclidien ${\displaystyle \mathbb {R} ^{n}}$ et un polytope P de ${\displaystyle \mathbb {R} ^{n}}$dont tous les sommets sont des points du réseau (par exemple , on utilise fréquemment le réseau ${\displaystyle {\mathcal {L}}=\mathbb {Z} ^{n}}$et des polytopes dont tous les sommets ont des coordonnées entières), engendrant un sous-espace affine de dimension d (d est appelé la dimension de P). Pour tout entier positif t, soit tP le polytope obtenu par dilatation de P par un facteur t, c'est-à-dire le polytope obtenu en multipliant par t les coordonnées de tous les sommets (exprimés dans une base du réseau, et soit ${\displaystyle L(P,t)=\#\left(tP\cap {\mathcal {L}}\right)}$ le nombre de points du réseau contenus dans le polytope tP. Ehrhart (en) montra en 1962 que L est un polynôme en t de degré d, c'est-à-dire qu'il existe des nombres rationnels ${\displaystyle L_{0}(P),\dots ,L_{d}(P)}$ tels que ${\displaystyle L(P,t)=L_{d}(P)t^{d}+L_{d-1}(P)t^{d-1}+\cdots +L_{0}(P)}$ pour tout entier t.

Le polynôme d'Ehrhart de l'intérieur d'un polytope convexe P de dimension d vérifie ${\displaystyle L(\operatorname {int} (P),t)=(-1)^{d}L(P,-t),}$ résultat connu sous le nom de réciprocité d'Ehrhart–Macdonald[1].

Le dilaté correspondant à ${\displaystyle t=2}$d'un carré unité contient ${\displaystyle (t+1)^{2}=9}$ points entiers.

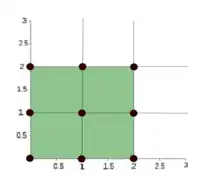
Soit P un hypercube unité de dimension d, dont les sommets sont les points dont toutes les coordonnées valent 0 ou 1, autrement dit ${\displaystyle P=\left\{x\in \mathbb {R} ^{d}:0\leq x_{i}\leq 1;1\leq i\leq d\right\}.}$

La dilatation de P par t est un hypercube de côté t, contenant (t + 1)^d points entiers, et donc le polynôme d'Ehrhart de P est L(P,t) = (t + 1)^d[2] - [3]. On voit aussi qu'aux entiers négatifs, on a${\displaystyle L(P,-t)=(-1)^{d}(t-1)^{d}=(-1)^{d}L(\operatorname {int} (P),t),}$ comme le prédit la réciprocité d'Ehrhart–Macdonald.

Bien d'autres nombres figurés peuvent s'exprimer à l'aide de polynômes d'Ehrhart. Par exemple, les nombres pyramidaux carrés sont donnés par le polynôme d'Ehrhart d'une pyramide à base carrée de côtés et de hauteur 1 ; le polynôme d'Ehrhart est dans ce cas 1/6(t + 1)(t + 2)(2t + 3)[4].

Soit P un polytope rationnel convexe, c'est-à-dire que ${\displaystyle P=\left\{x\in \mathbb {R} ^{d}:Ax\leq b\right\},}$ avec ${\displaystyle A\in \mathbb {Q} ^{k\times d}}$ et ${\displaystyle b\in \mathbb {Q} ^{k}}$ (cela revient à dire que P est l'enveloppe convexe d'un ensemble fini de points de ${\displaystyle \mathbb {Q} ^{d}}$). Posons ${\displaystyle L(P,t)=\#\left(\left\{x\in \mathbb {Z} ^{n}:Ax\leq tb\right\}\right)}$, le nombre de points entiers contenus dans tP. Dans ce cas, L(P, t) est un quasi-polynôme (en) en t, c'est-à-dire que ${\displaystyle L(P,t)=c_{d}(t)t^{d}+c_{d-1}(t)t^{d-1}+\cdots +c_{0}(t)}$, où les ${\displaystyle c_{i}(t)}$ sont des fonctions périodiques de période entière. La loi de réciprocité d'Ehrhart–Macdonald est encore valable : on a ${\displaystyle L(\operatorname {int} (P),t)=(-1)^{n}L(P,-t)}$.

Soit P un quadrilatère de sommets (0,0), (0,2), (1,1) et (3/2, 0). Le nombre de points entiers dans tP est donné par le quasi-polynôme ${\displaystyle L(P,t)={\frac {7t^{2}}{4}}+{\frac {5t}{2}}+{\frac {7+(-1)^{t}}{8}}}$[5].

Si P est fermé (c'est-à-dire que les faces de la frontière appartiennent à P), certains coefficients de L(P, t) ont une interprétation simple :

• le coefficient dominant, ${\displaystyle L_{d}(P)}$, est égal au volume d-dimensionnel de P, divisé par ${\displaystyle v({\mathcal {L}})}$, le covolume du réseau ${\displaystyle {\mathcal {L}}}$ ;
• le second coefficient, ${\displaystyle L_{d-1}(P)}$, peut se calculer en partant des réseaux ${\displaystyle {\mathcal {L}}_{F}}$ induits par ${\displaystyle {\mathcal {L}}}$ sur les faces F de P : ${\displaystyle L_{d-1}(P)}$ est obtenu en divisant le (d-1)-volume de chaque face F par ${\displaystyle 2v({\mathcal {L}}_{F})}$, et en faisant la somme de ces nombres pour toutes les faces de P ;
• le coefficient constant a₀ est la caractéristique d'Euler de P ; dans le cas convexe et fermé, on a ${\displaystyle L_{0}(P)=1}$

La série génératrice des polynômes d'Ehrhart pour un polytope P de dimension d est ${\displaystyle \operatorname {Ehr} _{P}(z)=\sum _{t\geq 0}L(P,t)z^{t}}$.

Cette série est une fraction rationnelle ; plus précisément, Ehrhart a démontré qu'il existe des nombres complexes ${\displaystyle h_{j}^{*}}$ (dépendants de P) tels que ${\displaystyle \operatorname {Ehr} _{P}(z)={\frac {\sum _{j=0}^{d}h_{j}^{\ast }z^{j}}{(1-z)^{d+1}}},\qquad \sum _{j=0}^{d}h_{j}^{\ast }\neq 0.}$

De plus, le théorème de non-négativité de Richard Stanley affirme que sous ces hypothèses, les ${\displaystyle h_{j}^{*}}$ sont des entiers naturels.

Un autre résultat de Stanley montre que si P iest un polytope contenu dans Q (sur le même réseau, on a ${\displaystyle h_{j}^{*}(P)\leq h_{j}^{*}(Q)}$ pour tout j[6].

On peut déterminer des bornes pour les coefficients non dominants ${\displaystyle c_{0},\dots ,c_{d-1}}$de la représentation ${\displaystyle L(P,t)=\sum _{r=0}^{d}c_{r}t^{r}}$ : on a par exemple[9] ${\displaystyle c_{r}\leq (-1)^{d-r}{\begin{bmatrix}d\\r\end{bmatrix}}c_{d}+{\frac {(-1)^{d-r-1}}{(d-1)!}}{\begin{bmatrix}d\\r+1\end{bmatrix}}}$, où ${\displaystyle \left[{\begin{smallmatrix}n\\k\end{smallmatrix}}\right]}$ est un nombre de Stirling de première espèce ; des bornes inférieures existent également[10]

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Ehrhart polynomial » (voir la liste des auteurs).

• Eugène Ehrhart, « Sur les polyèdres rationnels homothétiques à n dimensions », Comptes rendus de l'académie des Sciences, vol. 254,‎ 1962, p. 616–618 (MR 0130860)
• (en) Ricardo Diaz et Sinai Robins, « The Ehrhart polynomial of a lattice n-simplex », Electronic Research Announcements of the American Mathematical Society, vol. 2,‎ 1996, p. 1–6 (DOI 10.1090/S1079-6762-96-00001-7, MR 1405963)
• (en) Matthias Beck, Jesús A. De Loera, Mike Develin, Julian Pfeifle et Richard P. Stanley, « Integer Points in Polyhedra—Geometry, Number Theory, Algebra, Optimization », Contemporary Mathematics, Providence, RI, American Mathematical Society, vol. 374,‎ 2005, p. 15–36 (MR 2134759)
• (en) Mircea Mustață, « Lecture notes on toric varieties », février 2005
• (en) Matthias Beck et Sinai Robins, Computing the Continuous Discretely: Integer-Point Enumeration in Polyhedra, New York, Springer-Verlag, coll. « Undergraduate Texts in Mathematics », 2007 (ISBN 978-0-387-29139-0, MR 2271992)
• (en) Jesús A. De Loera, Jörg Rambau et Francisco Santos, Triangulations: Structures for Algorithms and Applications, vol. 25, Springer, coll. « Algorithms and Computation in Mathematics », 2010 (ISBN 978-3-642-12970-4, lire en ligne), p. 475
• (en) Richard J. Mathar, Point counts of ${\displaystyle D_{k}}$ and some ${\displaystyle A_{k}}$ and ${\displaystyle E_{k}}$ integer lattices inside hypercubes, 2010 (Bibcode 2010arXiv1002.3844M, arXiv 1002.3844)
• Hélène Chakroun, « Le théorème d'Ehrhart », sur Université Grenoble-Alpes, 22 mai 2017