Plongement lexical

De façon générale, la technique des plongements lexicaux est possible grâce à l'hypothèse distributionnelle (distributional hypothesis), établie dans le domaine de la sémantique distributionnelle (en). L’idée est que des mots de sens proches auront tendance à apparaître dans des voisinages de mots similaires. Comme l'a écrit John Rupert Firth en 1957, « Vous connaîtrez un mot par ses fréquentations. »[6]. En utilisant le voisinage d'un mot pour représenter ce dernier, on crée ainsi une représentation qui peut encoder sa sémantique (son sens). En d'autres termes, le contexte suffit pour représenter un mot, ce qui est fort différent de la linguistique traditionnelle chomskienne.

D'un point de vue historique, l’encodage des mots selon certaines caractéristiques de leur sens a commencé dans les années 1950 et 1960. En particulier, le modèle vectoriel en recherche d’information permet de représenter un document complet par un objet mathématique qui vise à rendre compte de son sens. Avec ces représentations de documents, on peut notamment concevoir un moteur de recherche plein texte, qui compare la représentation d’une requête utilisateur avec les représentations de multiples documents. La représentation la plus proche de celle de la requête correspond alors au document le plus pertinent[7].

On distingue deux approches pour encoder le contexte (le voisinage) d'un mot. Les approches à base de fréquences dénombrent les mots cooccurrents avec un mot donné, puis distillent cette information pour créer des vecteurs denses et de petite dimension. Un exemple est l'analyse sémantique latente[4]. Les plongements lexicaux constituent une seconde approche, prédictive celle-là, par laquelle on cherche à prédire un mot donné à l'aide de son contexte[8] ou vice-versa. C'est ce processus qui engendre les plongements lexicaux. Une implémentation populaire du calcul des plongements de mots est fournie par le chercheur Tomas Mikolov dans son programme word2vec[9] - [10], dont la description date de 2013[9].

L'idée générale est de projeter un ensemble de mots d'un vocabulaire de taille ${\displaystyle V}$dans un espace vectoriel continu où les vecteurs de ces mots ont une taille ${\displaystyle N}$ relativement petite. De plus, on veut trouver une représentation vectorielle de chaque mot de ${\displaystyle V}$de façon que les mots aux représentations voisines apparaissent dans des contextes similaires[11].

L'approche de Mikolov s'appuie sur des réseaux de neurones artificiels pour construire ces vecteurs. Ces modèles sont entraînés sur des corpus très volumineux. Le principe de base est qu'on tente de prédire un mot à partir de son contexte ou vice-versa. Un sous-produit de cet apprentissage constitue les plongements lexicaux. Il existe deux variantes de l'algorithme word2vec. Le modèle continuous bag-of-words (sac de mots continu) cherche à prédire un mot à partir de ses mots voisins, par exemple prédire attrape dans l'extrait le chat ____ la souris. Le modèle skip-gram cherche à prédire les mots du contexte à partir d'un mot central, par exemple prédire les quatre mots le, chat, la et souris à partir de attrape[4].

Modèle CBOW. Illustration adaptée de l'article de Mikolov[9].

Modèle skip-gram. Illustration adaptée de l'article de Mikolov[9].

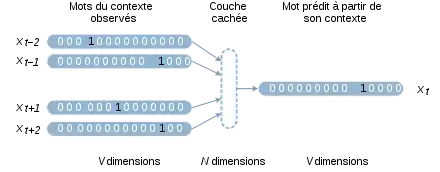
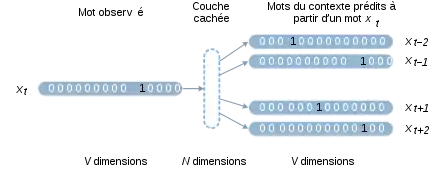
Dans les deux cas, on définit un réseau de neurones artificiels qui a une couche d'entrée ${\displaystyle X}$, et une couche de sortie ${\displaystyle Y}$. Ces vecteurs sont binaires et de taille ${\displaystyle V}$. Une couche cachée à ${\displaystyle N}$dimensions est intercalée entre les deux. ${\displaystyle N}$ est un hyperparamètre d'apprentissage. L'entraînement du réseau produit une matrice ${\displaystyle W}$ de taille ${\displaystyle V\times N}$, connectée à gauche aux entrées et à droite à la couche cachée. Au terme de l'apprentissage, la matrice ${\displaystyle W}$ contient les plongements de tous les mots du vocabulaire.

Les vecteurs ${\displaystyle X}$ et ${\displaystyle Y}$sont construits avec un encodage one-hot : ils possèdent un unique 1 dans leur i^ème dimension et des zéros partout ailleurs. La dimension i non nulle correspond au mot i du vocabulaire. À la suite de la multiplication matricielle, la i^ème ligne de ${\displaystyle W}$encode donc le plongement du i^ème mot. La propagation consiste à mettre à jour les différentes couches du réseau. La couche cachée est une application linéaire des entrées ${\displaystyle X}$ et de la couche ${\displaystyle W}$. La couche de sortie ${\displaystyle Y}$ est calculée grâce à la fonction softmax. La rétro-propagation utilise une fonction de perte ${\displaystyle E}$, qui spécifie un score suivant la sortie en sachant l'entrée ${\displaystyle X}$[12].

réseau de neurones skip-gram

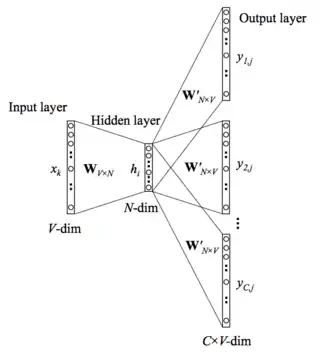
Le modèle skip-gram[9] apprend en considérant un mot tiré d'une phrase donnée. Autrement dit pour entraîner le réseau de neurones nous considérons une phrase ${\displaystyle p}$, on en extrait un mot ${\displaystyle m_{i}}$ qui sera notre entrée du réseau ${\displaystyle \{x_{k}\}}$. Le reste de la phrase sera notre sortie ${\displaystyle \{y_{1},..,y_{c}\}}$.

La couche cachée ${\displaystyle h}$ est dans ce cas la somme pondérée de l'entrée ${\displaystyle X}$ par ${\displaystyle W}$, seuls les éléments non nuls de ${\displaystyle X}$ apportent de l'information, on peut donc montrer que: ${\displaystyle h=X^{T}W=W_{(k,.)}=v_{w_{I}}}$.

La couche de sortie ${\displaystyle Y}$ peut être calculée sur la même idée, on a donc que l'entrée à la ${\displaystyle j}$-ième valeur du ${\displaystyle c}$-ième mot est: ${\displaystyle u_{cj}=v'{^{T}_{w_{j}}}h}$

Nous pouvons donc appliquer la fonction fonction softmax. qui nous donne ${\displaystyle p(w_{c,j}=w_{O,c}|w_{i})=y_{c,j}={\frac {exp(u_{c,j})}{\sum _{j=1}^{V}exp(u_{j'})}}}$

La fonction de perte est définie comme étant ${\displaystyle E=-\log p(w_{0,1},..,w_{0,c}|w_{I})}$.

réseau de neurones Continuous Bag-of-words

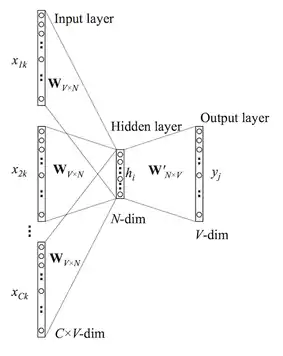
Le modèle Continuous Bag-of-words[9] est l'image inverse du skip-gram modèle. À partir d'un contexte ${\displaystyle \{x_{i},..,x_{c}\}}$ il apprend à reconnaître un mot ${\displaystyle y_{j}}$, l'ensemble ${\displaystyle \{xi,..,x_{c}\}\bigcup \{y_{j}\}}$ est une phrase du langage.

Comme dans le modèle Skip-gram la couche cachée ${\displaystyle h}$ est la somme pondérée de l'entrée ${\displaystyle X}$ par ${\displaystyle W}$, on peut donc montrer que: ${\displaystyle h={\frac {1}{C}}W.\sum _{i=1}^{C}x_{i}}$.

La couche de sortie ${\displaystyle Y}$ peut être calculée sur la même idée, on a donc que l'entrée à la ${\displaystyle j}$-ième valeur du mot est: ${\displaystyle u_{j}=v'{^{T}_{w_{j}}}.h}$

Nous pouvons donc appliquer la fonction fonction softmax qui nous donne ${\displaystyle p(w_{y_{j}|w_{1},..,w_{C}})=y_{j}={\frac {\exp(u_{j})}{\sum _{j=1}^{V}\exp(u'_{j})}}}$

La fonction de perte est définie comme étant ${\displaystyle E=-\log p(w_{O}|w_{I})}$.

Les premiers outils de traduction se basent sur des corpus parallèles afin d'apprendre les traductions mot à mot. Cette méthode étant très limitée (par exemple small peut être traduit par petit, petite, petites ou petits en fonction du contexte, ce qui n'est pas étudié dans le cas présent), la méthode a évolué en étudiant les bigrammes ou trigrammes afin de replacer chaque mot dans son contexte. La traduction est ainsi largement améliorée mais reste approximative car il n'y a aucune analyse sémantique des phrases.

L'analyse sémantique est difficilement réalisable à partir des mots seuls. La traduction étant l'étude sémantique des similarités entre deux langages, cela rajoute encore une difficulté. Le plongement lexical permet une traduction automatique à partir des similarités sémantiques entre les langages.

La traduction avec le plongement lexical se fait en plusieurs temps :

• plongement lexical sur chacun des deux langages (apprentissage de la sémantique de chaque langage)
• plongement lexical bilingue (apprentissage des similarités inter-langages)

Le plongement lexical bilingue nécessite deux étapes :

• l'initialisation
• l'entrainement.

Lors de l'initialisation, le coefficient d'alignement de chaque mot d'un langage avec les mots de l'autre langage est calculé, c'est-à-dire le nombre de fois où chaque mot x est aligné avec chaque mot y (et donc apparaît au même endroit dans les deux textes) par rapport au nombre de fois où le mot x apparaît dans toutes les sources.

On crée ainsi une matrice d'alignement où chaque ${\displaystyle a_{ij}}$ correspond au coefficient d'alignement du i^ème mot du premier langage avec le j^ème mot du deuxième langage.

Enfin, pour l'entrainement, on calcule un vecteur objectif qui se base sur la matrice d'alignement précédemment calculée et sur les apprentissages de chaque langage. Ce vecteur servira de vecteur objectif lors de l'entrainement du plongement lexical bilingue.

Avec l'arrivée des réseaux sociaux, l'analyse automatique de sentiments (opinion mining) est devenue un domaine de recherche très étudié, le but étant de déduire si une phrase est plutôt positive, négative ou neutre. Cette analyse est notamment utilisée dans l'analyse de tweets.

Avant l'arrivée du plongement lexical, l'analyse automatique de sentiments se basait sur une base d'apprentissage annotée entièrement à la main.

Le plongement lexical apporte donc une véritable aide pour l'analyse de sentiments car il permet d'éviter une partie importante de travail manuel.

Le plongement lexical ne peut pas être utilisé tel quel. Il comporte, en effet, une approche sémantique, or, avec cette approche, les mots bon et mauvais, par exemple, seront très proches alors que l'analyse de sentiment les voudrait opposés. Il faut donc ajouter dans la représentation de chaque mot un apprentissage spécifique aux sentiments.

Pour cela, en plus du plongement lexical sémantique, s'ajoute un plongement lexical qui étudie les sentiments dans une phrase ainsi qu'un dernier qui va permettre de mêler ces deux plongements lexicaux.

Le plongement lexical qui permet d'étudier les sentiments se base sur les mêmes éléments qu'un plongement lexical sémantique, c'est-à-dire le même réseau de neurones.

Chaque séquence de mot va être étudiée à l'aide d'une fenêtre glissante, c'est-à-dire qu'on étudie n-gramme par n-gramme. La dernière couche du réseau de neurones, qui se base sur des probabilités conditionnelles, calcule la probabilité totale (pour la somme de tous les n-grammes de la séquence de mots) d'avoir une séquence de mot positive ou négative, cette probabilité donne directement la prédiction voulue.

Le plongement lexical sémantique ne prend pas en compte les sentiments, tandis que le plongement lexical de sentiments ne prend pas en compte la sémantique. On peut donc les unifier en considérant une fonction de coût qui correspond à une combinaison linéaire des deux fonctions de coûts.

Pour l'entraînement, la base d'apprentissage se base sur un corpus distant-supervisés grâce à des émoticônes positives et négatives, c'est-à-dire un corpus n'étant pas étiqueté à la main mais grâce à une heuristique ayant un minimum de connaissance (ici la connaissance de l'heuristique est le sentiment en fonction de quelques émoticônes).

Les principaux problèmes de la reconnaissance vocale sont : le coût, le temps de collecte et d'annotation des données et la mise à jour des données.

Le plongement lexical permet de contrer l'ensemble de ces inconvénients.

L'utilisation du plongement lexical se fait ici de deux manières : une première étape permet de reconnaître la phonétique de la phrase, une seconde permet d'apprendre à reconnaître de nouveaux mots.

Entraînement du plongement lexical pour la reconnaissance vocale.

Lors de la première étape, un flux de parole correspondant à une phrase exprimée par l'utilisateur est donné en entrée. Le plongement lexical est d'abord entraîné pour trouver le prochain mot d'une phrase à partir d'un corpus de textes. Afin de déterminer chaque mot, le début de la phrase déjà analysée et la phonétique partant du début jusqu'à la fin du mot à analyser est donné en entrée. Cela permet de calculer la probabilité avec une fonction softmax de chaque mot possible à partir de sa phonétique, afin de déterminer le mot le plus probable.

Cette technique n'est, cependant, pas suffisante car les mots détectés doivent exclusivement faire partie des corpus utilisés lors de l'entrainement.

Ce problème est réglé par l'ajout d'un deuxième plongement lexical qui ne travaille pas sur la sémantique mais sur les mots proches phonétiquement. Ce dernier se base sur les ensembles de lettres. Par exemple, le mot "hello" est décomposé comme suit : {h, e, l, o, [h, he, el, lo, o], [he, hel, ell, llo, lo], . . . }. Afin de l’entraîner, deux plongements lexicaux phonétiques et un acoustique sont utilisés (voir figure ci-contre). Le flux de parole correspondant à un mot est envoyé en entrée du plongement lexical acoustique, puis deux mots pouvant correspondre (le bon mot ainsi qu'un mauvais) sont envoyés aux deux autres. Un tel entraînement permet de comprendre d'autres mots et permet d'apprendre les mots proches phonétiquement car leurs vecteurs ainsi calculés sont très proches.

L'espace appris par les méthodes traditionnelles n'est pas interprétable, il est généralement impossible d'interpréter le sens de chacune des dimensions pour un humain. Néanmoins, certaines méthodes de la littérature permettent de construire des plongements interprétables. Les travaux de Murphy et al.[13] sont pionniers en ce sens, avec leur approche Non negative sparse embedding (NNSE), ils proposent de factoriser la matrice de co-occurrences en introduisant des termes de régularisation pour forcer l'apprentissage d'un espace dans lequel les vecteurs sont creux. Par la suite, Faruqui et al.[14] avec Spowv et Subarmanian et al.[15] avec Spine ont proposé des approches qui reprennent cette idée. En revanche, Spine se base sur des architectures plus récentes, introduisant un auto-encodeur permettant d'obtenir de telles représentations creuses. Prouteau et al.[16] proposent eux d'apprendre ces représentations via une approche basée graphe à la faible complexité, permettant un calcul très rapide de ces vecteurs dont l'interprétabilité est évaluée[17].