Modèle vectoriel

Le modèle vectoriel est une représentation mathématique du contenu d'un document, selon une approche algébrique.

L'ensemble de représentation des documents est un vocabulaire comprenant des termes d'indexation. Ceux-ci sont typiquement les mots les plus significatifs du corpus considéré : noms communs, noms propres, adjectifs... Ils peuvent éventuellement être des constructions plus élaborées comme des expressions ou des entités sémantiques. À chaque élément du vocabulaire est associé un index unique arbitraire.

Chaque contenu est ainsi représenté par un vecteur v, dont la dimension correspond à la taille du vocabulaire. Chaque élément v_i du vecteur v consiste en un poids associé au terme d'indice i et à l'échantillon de texte. Un exemple simple est d'identifier v_i au nombre d'occurrences du terme i dans l'échantillon de texte. La composante du vecteur représente donc le poids du mot ${\displaystyle i}$ dans le document. L'un des schémas de pondération les plus usités est le TF-IDF.

Étant donné une représentation vectorielle d'un corpus de documents, on peut introduire une notion d'espace vectoriel sur l'espace des documents en langage naturel. On en arrive à la notion mathématique de proximité entre documents.

Représentation de deux documents (${\displaystyle d_{1}}$ et ${\displaystyle d_{2}}$) et d'une requête (${\displaystyle q}$) dans un espace vectoriel. La proximité de la requête aux documents est représentée par les angles ${\displaystyle \alpha }$ et ${\displaystyle \theta }$ entre les vecteurs.

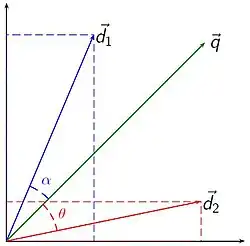
En introduisant des mesures de similarité adaptées, on peut quantifier la proximité sémantique entre différents documents. Les mesures de similarité sont choisies en fonction de l'application. Une mesure très utilisée est la similarité cosinus, qui consiste à quantifier la similarité entre deux documents en calculant le cosinus entre leurs vecteurs. La proximité d'une requête ${\displaystyle q}$ à un document ${\displaystyle d_{1}}$ sera ainsi donnée par:

${\displaystyle \cos {\alpha }={\frac {\mathbf {d_{1}} \cdot \mathbf {q} }{\left\|\mathbf {d_{1}} \right\|\left\|\mathbf {q} \right\|}}}$

En conservant le cosinus, nous exprimons bien une similarité. En particulier, une valeur nulle indique que la requête est strictement orthogonale au document. Physiquement, cela traduit l'absence de mots en commun entre ${\displaystyle q}$ et ${\displaystyle d_{1}}$. De plus, cette mesure n'est pas sensible à la norme des vecteurs, donc ne tient pas compte de la longueur des documents.

Un avantage de la similarité cosinus est qu'elle peut efficacement profiter d'une implémentation par index inversé à condition d'indexer également la norme des documents. Chaque élément non nul de la requête ${\displaystyle q}$ permet de retrouver des documents potentiellement pertinents et le produit scalaire (numérateur de la similarité cosinus) est simultanément calculé par accumulation « en ligne ».

Une alternative tout aussi efficace est de calculer le carré de la norme L2 entre ${\displaystyle q}$ et ${\displaystyle d_{1}}$ exprimée par:

${\displaystyle \|\mathbf {q-d_{1}} \|_{2}^{2}=\|\mathbf {q} \|_{2}^{2}+\|\mathbf {d_{1}} \|_{2}^{2}-2\mathbf {d_{1}} \cdot \mathbf {q} }$

Cette approche dépendant des mêmes grandeurs que la similarité cosinus, elle est aussi efficace à calculer via une implémentation par index inversé.

Parmi les applications existantes, on peut citer :

• la catégorisation : regrouper automatiquement des documents dans des catégories prédéfinies.
• la classification : étant donné un ensemble de documents, déterminer automatiquement les catégories qui permettront de séparer les documents de la meilleure façon possible (catégorisation non supervisée).
• la recherche documentaire : trouver les documents qui répondent le mieux à une requête (ce que fait un moteur de recherche) ; la requête de l'utilisateur est considérée comme un document, traduite en vecteur, et comparée aux vecteurs contenus dans le corpus des documents indexés.
• Le filtrage : classer à la volée des documents dans des catégories prédéfinies (par exemple, identifier un spam sur la base d'un nombre suspect d'occurrence du mot « pénis » dans un courriel et l'envoyer automatiquement à la corbeille).

Le modèle vectoriel est relativement simple à appréhender (algèbre linéaire) et est facile à implémenter. Il permet de retrouver assez efficacement des documents dans un corpus non structuré (recherche d'information), son efficacité dépendant pour une grande part de la qualité de la représentation (vocabulaire et schéma de pondération). La représentation vectorielle permet aussi une mise en correspondance des documents avec une requête imparfaite.

Il comporte également plusieurs limitations qui furent, pour certaines, corrigées par des affinements du modèle. En particulier, ce modèle suppose que les termes représentatifs sont indépendants. Ainsi, dans un texte, l'ordre des mots n'est pas pris en compte. Dans sa version la plus simple, il ne prend pas non plus en compte les synonymes ou la morphologie des contenus.