Fonction softmax

En mathématiques, la fonction softmax, aussi appelée fonction softargmax[2]^:184 ou fonction exponentielle normalisée[3]^:198, est une généralisation de la fonction logistique. Elle convertit un vecteur de $K$ nombres réels en une distribution de probabilités sur $K$ choix. Plus précisément, un vecteur $\mathbf {z} =\left(z_{1},\dots ,z_{K}\right)$ est transformé un vecteur $\sigma \left(\mathbf {z} \right)$ de $K$ nombres réels strictement positifs et de somme 1. La fonction est définie par :

\sigma (\mathbf {z} )_{j}={\frac {\mathrm {e} ^{z_{j}}}{\sum _{k=1}^{K}\mathrm {e} ^{z_{k}}}}

pour tout

j\in \left\{1,\ldots ,K\right\}

Fonction softmax utilisée après un CNN (Réseau neuronal convolutif). Ici le vecteur (35.4, 38.1, -5.0) est transformée en (0.06, 0.94, 0.00). Dans ce contexte de classification d'images, le chien est reconnu[1].

c'est-à-dire que la composante $j$ du vecteur $\sigma (\mathbf {z} )$ est égale à l'exponentielle de la composante $j$ du vecteur $z$ divisée par la somme des exponentielles de toutes les composantes de $z$ .

En théorie des probabilités, la sortie de la fonction softmax peut être utilisée pour représenter une loi catégorielle – c’est-à-dire une loi de probabilité sur $K$ différents résultats possibles. La fonction softmax est également connue pour être utilisée dans diverses méthodes de classification en classes multiples, par exemple dans le cas de réseaux de neurones artificiels. Cette fonction est parfois considérée pour une version régulière de la fonction argmax[4] : si une composante $z_{j}$ est strictement plus grande que les autres composantes $z_{k}$ , alors $\sigma (\mathbf {z} )_{j}$ vaut presque 1 et $\sigma (\mathbf {z} )_{k}$ est quasiment nulle pour tout $k\neq j$ .

Exemple

Considérons un vecteur

\mathbf {z} =\left(1~;~3~;~2,\!5~;~5~;~4~;~2\right)

de six nombres réels. La fonction softmax donne en sortie (tronquée à 10^-2) :

\sigma (\mathbf {z} )=(0,\!01~;~0,\!08~;~0,\!04~;~0,\!60~;~0,\!22~;~0,\!03)

Apprentissage

Régression logistique

Une utilisation courante de la fonction softmax apparaît dans le champ de l'apprentissage automatique, en particulier dans la régression logistique : on associe à chaque possibilité de sortie un score, que l'on transforme en probabilité avec la fonction softmax. L'intérêt de cette fonction est qu'elle est différentiable, et s'avère donc compatible avec l'algorithme du gradient.

Concrètement, on a en entrée un vecteur, qui est donc une matrice colonne, notée $x$ , de $N$ lignes. On va la multiplier par une matrice dite « de poids » $W$ de $T$ lignes et de $N$ colonnes, afin de transformer $x$ en un vecteur de $T$ éléments (appelés logits). La fonction softmax est utilisée pour transformer les logits dans un vecteur de probabilités, indiquant la probabilité que $x$ appartienne à chacune des classes de sortie $T$ .

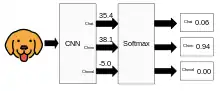
Par exemple, si on donne en entrée la couleur des pixels d'une image de chat, on aura pour chaque ligne de $W$ des nombres, des « poids », propres à chaque animal, et ainsi chaque logit sera le score d'un animal. Si le score du chat est le plus important, alors la probabilité donnée par la fonction softmax que l'image est un chat sera la plus importante, d'après l'étude de la couleur des pixels. Mais on peut travailler sur d'autres caractéristiques, et ainsi obtenir d'autres probabilités, afin de déterminer l'animal sur la photo. Au fur et à mesure que l'intelligence artificielle aura d'exemples, plus la matrice de poids s'affinera, et plus le système sera performant : on parle d'apprentissage automatique.

Classification multi-classes

Pour faire de la classification multi-classes, on peut utiliser un perceptron dont la dernière couche contient autant de neurones que de classes. La fonction softmax est utilisée comme fonction d'activation dans l'architecture d'un perceptron multi-classe[4].

Lien avec la physique statistique

En physique statistique, la distribution de Maxwell est essentiellement une application de la fonction softmax aux niveaux d'énergie $E i$ possibles :

P_{i}={\mathrm {e} ^{-\beta E_{i}} \over \sum _{j}\mathrm {e} ^{-\beta E_{j}}}

En substance, l'idée est qu'un système en équilibre thermodynamique avec un environnement avec lequel il échange constamment de l'énergie, tendra à occuper les états d'énergie les plus bas, mais que cette tendance sera tout de même contrariée par le facteur $β$ , dit de température inverse. Le choix d'une température inverse revient en fait à choisir une base d'exponentielle pour la fonction softmax, qui garde néanmoins sa propriété de construction fondamentale.

Ceci est la raison pour laquelle en apprentissage automatique, un paramètre de température est introduit pour choisir le niveau d'uniformité de la distribution : plus la température sera élevée, plus les possibilités seront équiprobables, tandis qu'avec une température faible, les valeurs d'énergie faibles seront considérablement plus probables que toutes les autres.

Voir aussi

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Softmax function » (voir la liste des auteurs).

(en) Gian Carlo Cardarilli, Luca Di Nunzio, Rocco Fazzolari et Daniele Giardino, « A pseudo-softmax function for hardware-based high speed image classification », Scientific Reports, vol. 11, n^o 1,‎ 28 juillet 2021, p. 15307 (ISSN 2045-2322, DOI 10.1038/s41598-021-94691-7, lire en ligne, consulté le 15 juin 2023)
Ian Goodfellow, Yoshua Bengio et Aaron Courville, Deep Learning, MIT Press, 2016, 180–184 p. (ISBN 978-0-26203561-3, lire en ligne), « 6.2.2.3 Softmax Units for Multinoulli Output Distributions »
Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006 (ISBN 0-387-31073-8)
Chloé-Agathe Azencott, Introduction au Machine Learning, 3 juillet 2022 (lire en ligne), Chapitre 7, Définition 7.1 p. 102.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.