Phase-shift keying

Pour déterminer les erreurs de manière mathématique, voici les définitions utiles pour la suite :

• ${\displaystyle E_{b}}$ = énergie par bit
• ${\displaystyle E_{s}}$ = énergie-par-symbole = ${\displaystyle kE_{b}}$ avec k bits par symbole
• ${\displaystyle T_{b}}$ = durée d'un bit (inverse du débit binaire)
• ${\displaystyle T_{s}}$ = durée d'un symbole
• ${\displaystyle N_{0}/2}$ = densité spectrale de bruit (W/Hz)
• ${\displaystyle P_{b}}$ = probabilité d'une erreur de bit
• ${\displaystyle P_{s}}$ = probabilité d'une erreur de symbole

${\displaystyle Q(x)={\frac {1}{\sqrt {2\pi }}}\int _{x}^{\infty }e^{-{\frac {1}{2}}t^{2}}\,dt={\frac {1}{2}}\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right),\ x\geq 0}$.

Exemple de diagramme de constellation pour BPSK.

BPSK est la forme la plus simple du PSK. Elle utilise deux phases qui sont séparées de 180° ; on l'appelle également 2-PSK. Cette modulation est la plus robuste de toutes les PSK car il faut une grande déformation du signal pour que le démodulateur se trompe sur le symbole reçu. Cependant on ne peut moduler qu'un seul bit par symbole (voir le schéma), ce qui est un inconvénient pour les applications qui nécessitent un débit binaire élevé.

Le taux d'erreur binaire du BPSK peut être calculé ainsi :

${\displaystyle P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)}$

Comme il y a un bit par symbole, cela correspond également au taux d'erreur de symbole.

Diagramme de constellation pour QPSK (codage gray binaire).

Souvent connue sous le nom de 4-PSK ou QPSK, cette modulation utilise un diagramme de constellation à quatre points, à équidistance autour d'un cercle. Avec quatre phases, QPSK peut coder deux bits par symbole, cf. schéma code de Gray. Cela permet de multiplier le débit binaire par deux comparé à un système BPSK tout en maintenant la bande passante du signal, ou de maintenir le débit en réduisant la bande passante utilisée par deux.

Bien que le QPSK puisse être vu comme une modulation en quadrature, il est aussi simple de le considérer comme deux modulations indépendantes. Avec cette interprétation, les bits pairs (ou impairs) sont utilisés pour moduler la composante In-Phase(I), tandis que les bits impairs (ou pairs) sont utilisés pour la Quadrature-phase (Q). BPSK est utilisé sur les deux porteuses et peuvent être démodulées indépendamment.

La probabilité d'une erreur de bit en QPSK est la même qu'en BPSK :

${\displaystyle P_{b}=Q\left({\sqrt {\frac {2E_{b}}{N_{0}}}}\right)}$.

Cependant, avec deux bits par symbole, le taux d'erreur par symbole augmente :

${\displaystyle \,\!P_{s}}$	${\displaystyle =1-\left(1-P_{b}\right)^{2}}$
	${\displaystyle =2Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)-\left[Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)\right]^{2}}$.

Si le rapport signal sur bruit est élevé (comme c'est le cas en pratique pour des systèmes QPSK), la probabilité d'erreur symbole peut être approximée par :

${\displaystyle P_{s}\approx 2Q\left({\sqrt {\frac {E_{s}}{N_{0}}}}\right)=erfc\left({\sqrt {\frac {E_{s}}{2N_{0}}}}\right)=erfc\left({\sqrt {\frac {E_{b}}{N_{0}}}}\right)}$

Comme avec BPSK il y a un problème d'ambigüité sur la phase pour le receveur et l'encodage différentiel de QPSK est souvent utilisé en pratique.

Implémentation

L'implémentation de QPSK est plus générale et d'un ordre PSK plus élevé que BPSK. L'écriture des symboles liés au diagramme de constellation en termes de composantes sinus et cosinus est représentée par :

${\displaystyle s_{i}(t)={\sqrt {\frac {2E_{s}}{T}}}\cos \left(2\pi f_{c}t+(2i-1){\frac {\pi }{4}}\right),i=1,2,3,4}$.

Avec, donc, les quatre valeurs de phases suivantes : ${\displaystyle \pi /4}$, ${\displaystyle 3\pi /4}$, ${\displaystyle 5\pi /4}$ and ${\displaystyle 7\pi /4}$.

Les deux composantes du signal sont données par les fonctions de base suivantes :

${\displaystyle \phi _{1}(t)={\sqrt {\frac {2}{T_{s}}}}\cos(2\pi f_{c}t)}$

${\displaystyle \phi _{2}(t)={\sqrt {\frac {2}{T_{s}}}}\sin(2\pi f_{c}t)}$

La fonction de base ${\displaystyle \phi _{1}(t)}$ donne la composante I ou In-phase et ${\displaystyle \phi _{2}(t)}$ la composante Q ou Quadrature permettant ainsi de représenter les états de phase du signal par quatre points dans le diagramme de constellation (voir ci-dessus).

${\displaystyle \left(\pm {\sqrt {E_{s}/2}},\pm {\sqrt {E_{s}/2}}\right)}$.

Le facteur ${\displaystyle 1/2}$ indique que la puissance totale est également répartie entre les deux porteuses.

En comparant ces expressions avec celles de BPSK, on remarque que QPSK peut s'interpréter comme deux signaux BPSK indépendants. QPSK peut être implémenté de différentes façons. Le schéma ci-dessous représente la structure et les composantes principales de la transmission d'un signal modulé par QPSK. Les deux symboles correspondant chacun à un état de phase dans le diagramme de constellation BPSK (voir section 2) ne relève pas d'un scindage du débit binaire par porteuse comme montré dans le schéma ci-dessous.

Schéma de principe de la transmission du signal QPSK. Le train binaire entrant est partagé entre les composantes In-phase et Quadrature. Les trains de bits sortant du démultiplexeur sont modulés séparément à l'aide d'une fonction de base orthogonale. Dans cette implémentation, deux sinusoïdes sont utilisées. Par la suite, les deux signaux ainsi obtenus sont recombinés pour former le signal QPSK. Les encodeurs ne retournent pas de polarité à bit 0 (NRZ). Ceux-ci peuvent être placés devant la source de données binaires, mais ici, ils sont disposés après pour illustrer conceptuellement la différence entre les signaux numériques et analogiques contribuant à la modulation numérique.

Schéma de principe de la réception du signal QPSK. Les filtres peuvent être remplacés par des corrélateurs. Chaque dispositifs de détection utilise une valeur seuil de référence pour déterminer si un 1 ou un 0 est détecté.

Signaux QPSK dans le domaine temporel

Le signal à moduler représenté sur la figure ci-dessous est donné pour un train de bits aléatoire réparti sur l'intervalle de données Data. Les deux ondes porteuses situées dans la partie supérieure du schéma correspondent respectivement à la composante cosinus (I ou In-phase) et la composante sinus (Q ou Quadrature). Les bits impairs sont assignés à la composante In-phase et les bits pairs à la composante Quadrature (le premier bit est forcé à 1). La résultante de la somme des deux composantes I et Q donne le signal représenté en bas de la figure. Les sauts de phase sur chaque composante peuvent être considérés comme des changements de phase PSK survenant au démarrage d'une période binaire. La forme d'onde du haut prise isolément correspond à la description de BPSK donnée en section 2.

Diagramme temporel QPSK. Le train de bits est affiché sous l'axe des temps T. Les deux composantes du signal avec leurs bits d'affectation sont représentées dans la partie haute du diagramme. L'onde du bas correspond à la combinaison des deux composantes. Notez les changements brusques de phase pour certaines valeurs du temps T !

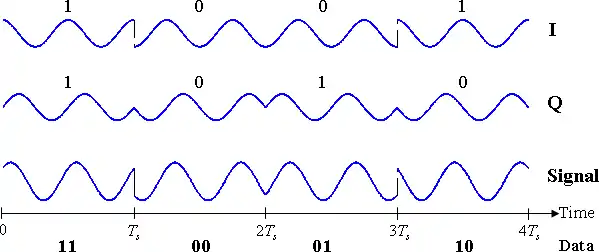
Ici, le mot binaire véhiculé par l'onde de forme est : 1 1 0 0 0 1 1 0.
Par rapport à ce mot binaire, on a :

• Bits impairs (en gras et soulignés) correspondant à la composante I ou In-phase : 1 1 0 0 0 1 1 0
• Bits pairs (en gras et soulignés) correspondant à la composante Q ou Quadrature : 1 1 0 0 0 1 1 0

${\displaystyle \pi /4}$–QPSK

Diagramme des deux constellations de phase pour π/4-QPSK. Cette figure montre deux constellations identiques avec code Gray décalées par rotation l'une par rapport l'autre de 45°.

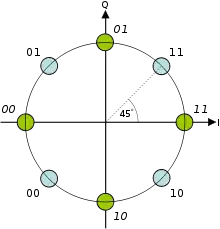
Cette dernière variante de QPSK utilise deux constellations identiques superposées et décalées par rotation l'une par rapport à l'autre de 45° (d'où le nom de ${\displaystyle \pi /4}$). Généralement, les bits pairs sont utilisés pour sélectionner les points d'une constellation et les bits impairs, les points de l'autre constellation. Dans ce cas, le décalage de phase est au maximum de 180° pour la phase qui correspond à l'un des points et de 135° pour la phase correspondant à l'autre point correspondant. La fluctuation d'amplitude est alors comprise entre OQPSK et QPSK non compensé.

Une des propriétés que possède ce type de modulation est que le signal modulé est représenté dans le plan complexe car il n'y aucune possibilité pour celui-ci de passer par l'origine. Ainsi, la plage de fluctuation du signal est réduite dynamiquement. Cette propriété est très intéressante pour l'ingénierie des signaux de communication.

D'autre part, ${\displaystyle \pi /4}$–QPSK se prête facilement à la démodulation et est utilisé, par exemple, dans les systèmes de multiplexage TDMA pour téléphone mobile.

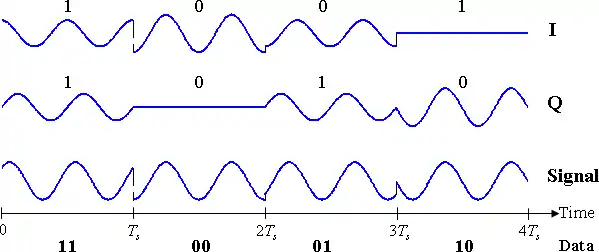
Le signal à moduler représenté sur la figure ci-dessous est donné pour un train de bits aléatoire réparti sur l'intervalle de données Data. La présentation du diagramme temporel est pratiquement la même que pour le QPSK à quatre points vu en section 3.2. Les symboles qui se succèdent sont issus du diagramme des deux constellations ci-contre. Ainsi, le premier symbole (1 1) est pris dans la constellation des points bleus et le second symbole (0 0) est tiré de la constellation des points verts. Notez que l'ordre de grandeur des deux ondes de forme change lorsqu'elles basculent entre les constellations pendant que l'amplitude totale du signal reste constante. Les décalages de phase sont entre celles des deux diagrammes temporels.

Diagramme temporel pour π/4-QPSK. Le train de bits est affiché sous l'axe des temps T. Les deux composantes du signal avec leurs bits d'affectation sont représentées dans la partie haute du diagramme. L'onde du bas correspond à la combinaison des deux composantes. Notons que la succession des symboles, à partir des deux constellations, se fait de manière alternative en commençant par un « bleu ».

Diagramme de constellation pour 8-PSK avec code de Gray.

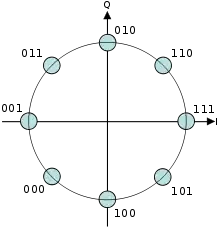
Il est possible de construire un diagramme de constellation PSK avec un nombre quelconque de phases. Mais, en pratique, 8-PSK est l'ordre le plus élevé dans l'élaboration d'un tel diagramme. En effet, avec plus de huit phases, la modulation PSK génère un taux d'erreur trop important. Il est nécessaire, pour aller au-delà de huit phases, d'utiliser un type de modulation plus complexe comme QAM (quadrature amplitude modulation). Même si un nombre quelconque de phases peut être employé, le fait que la constellation traite des données binaires signifie que le nombre de symboles est toujours obtenu à partir d'une puissance de 2 (ce qui représente un nombre égal de bits par symbole).

Pour ${\displaystyle M}$-PSK, il n'y a pas d'expression mathématique simple pour calculer le taux d'erreur si ${\displaystyle M>4}$. En effet, la seule expression générale permettant de représenter ce taux est :

${\displaystyle P_{s}=1-\int _{\frac {\pi }{M}}^{\frac {\pi }{M}}p_{\Theta _{r}}\left(\Theta _{r}\right)d\Theta _{r}}$

où

${\displaystyle p_{\Theta _{r}}\left(\Theta _{r}\right)={\frac {1}{2\pi }}e^{-2\gamma _{s}\sin ^{2}\Theta _{r}}\int _{0}^{\infty }Ve^{-\left(V-{\sqrt {4\gamma _{s}}}\cos \Theta {r}\right)^{2}/2}}$,

${\displaystyle V={\sqrt {r_{1}^{2}+r_{2}^{2}}}}$,

${\displaystyle \Theta _{r}=\tan ^{-1}\left(r_{2}/r_{1}\right)}$,

${\displaystyle \gamma _{s}={\frac {E_{s}}{N_{0}}}}$ et

${\displaystyle r_{1}\sim {}N\left({\sqrt {E_{s}}},N_{0}/2\right)}$ et ${\displaystyle r_{2}\sim {}N\left(0,N_{0}/2\right)}$ sont des variables aléatoires conjointes de Gauss.

Courbes du taux d'erreur binaire pour BPSK, QPSK, 8-PSK et 16-PSK. Le rapport signal/bruit en abscisse est exprimé en décibel.

L'expression mathématique de ${\displaystyle P_{s}}$ peut être approximée pour M et ${\displaystyle E_{b}/N_{0}}$ très élevés par :

${\displaystyle P_{s}\approx 2Q\left({\sqrt {2\gamma _{s}}}\sin {\frac {\pi }{M}}\right)}$.

La probabilité liée au taux d'erreur binaire pour ${\displaystyle M}$-PSK peut être déterminée dans la mesure où l'on connaît la cartographie binaire du signal. Toutefois, lorsque le code de Gray est utilisé, l'erreur probabiliste générée par le passage d'un symbole à l'autre est égale à une erreur binaire. Dans ce cas, on a l'approximation :

${\displaystyle P_{b}\approx {\frac {1}{k}}P_{s}}$.

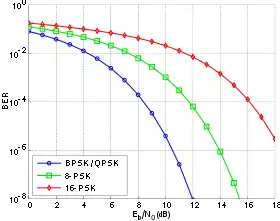
Le graphique de gauche compare le taux d'erreur binaire entre BPSK, QPSK (identique à BPSK), 8-PSK et 16-PSK. On constate sur celui-ci que les modulations d'ordre supérieur présentent un taux d'erreur plus important. En revanche, ce taux est constaté pour un train de données plus élevé.

Les limites sur taux d'erreur provenant de différents types de modulations numériques peuvent être précisées par application de l'inégalité de Boole au diagramme de constellation du signal.