Pendule de torsion
En physique, un pendule de torsion est un dispositif constitué d'une barre horizontale, fixée à un support par l'intermédiaire d'un fil de torsion. Ce fil d'acier exerce un couple de rappel, proportionnel à l'angle de torsion qu'on lui impose :
- .
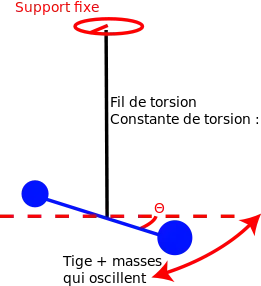
Sur la barre, on peut positionner deux masselottes de façon symétrique, afin de modifier le moment d'inertie.
Modèle sans frottements
Si on lâche le dispositif en l'ayant écarté — dans un plan horizontal — de sa position d'équilibre, celui-ci oscille dans ce plan. Dans des approximations acceptables, la période est indépendante de l’amplitude : on parle d'oscillations isochrones. On peut la calculer à partir de la formule ci-dessous :
où J désigne le moment d'inertie de la barre munie des masselottes.
Cette relation simplifiée provient de l'équation différentielle du mouvement, établie à partir du théorème du moment cinétique ou de la conservation de l'énergie mécanique, lorsqu'on considère les frottements négligeables. Si θ représente l'angle de torsion du fil, on a :
Le pendule de torsion est idéalement un oscillateur harmonique.

Modèle avec frottements
Si l'on veut tenir compte de la perturbation apportée par les frottements, par exemple exercés par l'air, on peut par exemple utiliser un modèle visqueux à faible vitesse, tel que le couple exercé s'oppose à la vitesse :
L'équation du mouvement s'écrit alors :
Ici, les oscillations sont amorties : on parle d'oscillations pseudo-périodiques.




