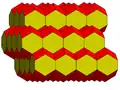
Pavage de l'espace

Dans cet emploi le terme pavage est une généralisation à trois dimensions du concept de pavage du plan, lequel dérive directement du sens commun de pavage, le recouvrement d'un sol par des pavés jointifs (des blocs de forme grossièrement cubique) : la surface d'un sol pavé se présente comme un assemblage de carrés jointifs.

En anglais on utilise le terme honeycomb (« nid d'abeille »), qui fait référence aux cellules de cire construites par les abeilles. En français on réserve plutôt le terme de nid d'abeille (ou d'abeilles) aux structures à base de prismes de section hexagonale.

Honeycomb en anglais, comme pavage en français, est aussi utilisé pour des espaces de dimension supérieure à 3, concurremment avec le terme tiling ou tessellation (« tuilage »). George Olshevsky a cependant plaidé pour limiter le terme honeycomb aux pavages tridimensionnels et développer une terminologie systématique pour les dimensions plus élevées : tetracomb pour les pavages d'un espace de dimension 4, pentacomb pour les pavages d'un espace de dimension 5, et ainsi de suite.

Il existe 28 pavages uniformes convexes (en) - l'ensemble des pavages uniformes dans l'espace tridimensionnel euclidien rempli par les cellules polyédriques uniformes convexes.

D'autres pavages isoédriques bien connus incluent le pavage dodécaédrique rhombique (en) et le pavage par des dodécaèdres rhombo-hexagonaux (en).

Les pavages les plus simples sont des couches empilées de prismes selon un pavage du plan. En particulier, pour chaque parallélépipède, chaque copie peut remplir l’espace, le pavage cubique (en) étant une forme régulière spéciale.

• 
  Pavage dodécaédrique rhombique (en).
• 
  Pavage cubique bitronqué (en).
• 
  Dodécaèdres rhombo-hexagonaux (en).
• 
  Pavage tétraédrique-octaédrique (en).
• 
  Pavage cubique (en).

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Honeycomb (geometry) » (voir la liste des auteurs).