Pas (sciences)
En sciences de l'ingénieur, le pas est la distance entre deux points de mesure ou de calcul. Il fait référence au découpage d'une longueur (respectivement : d'une surface ou d'un volume), en segments (respectivement en pavés, en cellules), et définit par là-même un treillis et des intervalles. Ce découpage permet de ramener l'information sur une grandeur variant de façon continue à travers l'espace, à l'information en certains points seulement, et donc de permettre un traitement (détection, calcul, affectation) sur un nombre de points fini. Le pas est la mesure fondamentale d'une opération de discrétisation.
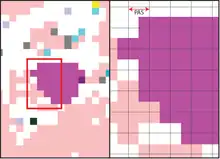
La taille du pas définit la résolution des données acquises ou la précision d'une activité mécanique ou numérique. On parle parfois, par une analogie mathématique avec le temps, de « période spatiale » et, réciproquement, de « pas de temps » pour désigner une période.
Exemples
Pour la réalisation d'une carte, un pas élevé permettra d'acquérir des données peu précises, mais couvrant une grande surface tandis qu'un pas faible couvrira une surface plus limitée, mais avec un niveau de détail plus élevé. La discrétisation permet par exemple de construire de manière approchée les courbes de niveau du relief, ainsi que les limites des strates dans une coupe géologique : les interfaces des strates ne sont en effet connues que par des sondages ponctuels, et le géologue formule implicitement une hypothèse de continuité de ces interfaces.

Les méthodes de calcul numérique par discrétisation : méthode des différences finies, méthode des éléments finis, méthode des volumes finis, etc. utilisent un maillage décrit par son pas. Une méthode numérique est dite convergente lorsque l'erreur d'approximation diminue avec le pas de discrétisation[1]. La réduction du pas de discrétisation est appelée raffinement h[2].
Pour les systèmes d'acquisition ou de fabrication automatisés le principe est le même : la machine fonctionnera par quadrillage de mesure dont la maille correspondra au pas choisi et ou chaque intersection sera un point de mesure (voir figure ci-dessus).
Références
- Philippe Ciarlet, Introduction à l'analyse numérique matricielle et à l'optimisation, Masson, coll. « Math. Appl. pour la Maîtrise », (réimpr. 2001) (ISBN 2-225-68893-1), « Origine des problèmes », p. 39
- (en) A. W. Craig, M. Ainsworth, J. Z. Zhu et O. C. Zienkiewicz, « h and h-p version error estimation and adaptive procedures from theory to practice. », Engineering with Computers, vol. 5, , p. 221–234