Orientation dans l'espace
L'orientation d'un objet dans l'espace est une partie de la description de la façon dont un objet est placé dans l'espace. Cette orientation est relative et ne peut être décrite que par rapport à une orientation de référence ; l'orientation est alors la rotation imaginaire que l'objet devrait subir pour être placé de la même façon que la référence. Une rotation n'est pas en général suffisante pour retrouver le placement de référence et il est le plus souvent nécessaire de faire subir une translation à l'objet, ce qui correspond à la position de l'objet dans l'espace.
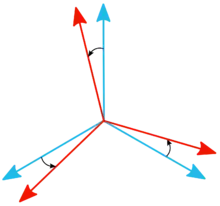
Repère lié à l'objet
Pour définir l'orientation d'un objet, la première étape consiste donc à définir deux vecteurs, c'est-à-dire deux axes orientés (c'est-à-dire munis d'un sens) non parallèles et liés à l'objet. Ces axes peuvent être choisis de manière arbitraire, ou bien suivre la forme ou l'anisotropie de l'objet. Par exemple, si l'objet est parallélépipédique, on choisira deux des arêtes de l'objet ; si l'objet est un cristallite, on choisira les deux directions ayant la plus grande densité d'atomes.
Cela revient en fait à définir un repère lié à l'objet, le troisième axe du repère pouvant être la normale au plan contenant les deux premiers axes.
Dans le plan (par exemple un piéton, ou un véhicule roulant sur terre), il suffit de définir un seul axe orienté pour l'objet.
Cas particulier du repère lié à la personne
Pour une personne, il est facile d'orienter les axes avant/arrière (face/dos) et, sauf cas inhabituel, l'axe dessus/dessous (tête/pieds) ; en raison de l'apparente symétrie du corps, il est moins évident d'orienter la dimension restante : la gauche peut alors être définie comme la direction qui vient compléter {vers le dessus, vers l'avant} pour former un trièdre direct.
Des phénomènes de désorientation spatiale (avec vertiges, éventuellement) peuvent affecter la personne dans le cas de certaines pathologies, de l'autisme, ou chez un pilote d'avion manquant des repères visuels habituellement disponibles au sol.
Rotations dans l'espace
L'orientation de référence peut être la coïncidence du repère lié à l'objet et du repère de référence considéré, ou bien l'orientation de l'objet à un instant donné.
Le passage de l'orientation de référence à l'orientation à l'instant considéré peut se faire par une rotation ρΔ(α) unique d'angle α donné selon un axe Δ donné (ceci est un résultat connu de la mécanique du solide). L'orientation peut donc être déterminée par la donnée de α et de , le vecteur directeur unitaire de Δ.
La rotation ρΔ(α) étant une application linéaire, elle est décrite par une matrice 3×3 g ; on peut donc également représenter l'orientation par la donnée de g.
Cependant, on utilise plus volontiers la donnée de trois angles, correspondant à trois rotations selon les axes liés à l'objet : les angles d'Euler (ψθφ). L'inconvénient est qu'une même orientation peut être définie par différents triplets d'angles d'Euler.
Rotation dans le plan
Dans le plan, il faut également définir un angle de rotation, mais il est inutile de définir l'axe : on peut prendre par convention la normale au plan (la verticale). On peut alors définir l'orientation par un seul chiffre, l'angle par rapport à l'axe objet-Nord.
Applications
Orientation en navigation
En navigation maritime et aérienne, on définit l'orientation par :
- la direction ou azimut, c'est-à-dire l'angle que fait l'axe arrière-avant du bateau ou de l'avion avec l'axe objet-Nord ; c'est l'angle d'Euler ψ ;
- le roulis, qui est la rotation autour de l'axe arrière-avant (le véhicule penche à gauche ou à droite) ; c'est l'angle d'Euler θ ;
- le tangage, qui est la rotation selon l'axe perpendiculaire à l'axe arrière-avant qui est horizontal dans la position de référence : l'axe des ailes pour un avion, la largeur du pont pour un bateau (le véhicule penche vers l'avant ou l'arrière) ; c'est l'angle d'Euler φ.
Orientation en anatomie
En anatomie, on s'intéresse en particulier aux mouvements des articulations. On prend comme référence la partie la plus proche du tronc lorsque cela est pertinent.
Les rotations portent le nom de flexion-extension, adduction-abduction, pronation-supination...
- Voir l'article détaillé Mouvement (anatomie).
