Ordre de domination

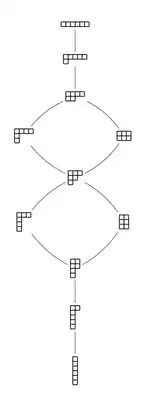
Soient ${\displaystyle p=(p_{1},p_{2},\ldots )}$ et ${\displaystyle q=(q_{1},q_{2},\ldots )}$ deux partitions d'un entier ${\displaystyle n}$, avec ${\displaystyle p_{1}\geq p_{2}\geq \cdots }$ et ${\displaystyle q_{1}\geq q_{2}\geq \cdots }$. Alors ${\displaystyle p}$ est inférieur ou égal à ${\displaystyle q}$ dans l'ordre de domination, et on écrit ${\displaystyle p\trianglelefteq q}$ si, pour tout ${\displaystyle k\geq 1}$, la somme des ${\displaystyle k}$ parties les plus grandes de ${\displaystyle p}$ est inférieure ou égale à la somme des ${\displaystyle k}$ plus grandes parties de ${\displaystyle q}$. Formellement : ${\displaystyle p\trianglelefteq q}$ si et seulement si, pour tout ${\displaystyle k\geq 1}$, ${\displaystyle p_{1}+\cdots +p_{k}\leq q_{1}+\cdots +q_{k}.}$

Dans cette définition, les partitions sont allongées si nécessaire en les complétant de parties nulles. Par exemple, et comme indiqué dans la figure, on a ${\displaystyle (6)\trianglerighteq (5,1)\trianglerighteq (4,2)\trianglerighteq \cdots \trianglerighteq (1,1,1,1,1,1)}$.

• Parmi les partitions d'un entier ${\displaystyle n}$, la partition ${\displaystyle (1,\ldots ,1)}$ est la plus petite, et ${\displaystyle (n)}$ la plus grande.
• L'ordre de domination implique l'ordre lexicographique. En d'autres termes, si ${\displaystyle p}$ domine ${\displaystyle q}$, alors ${\displaystyle p}$ est supérieur à ${\displaystyle q}$ dans l'ordre lexicographique, mais la réciproque n'est pas vraie : par exemple ${\displaystyle (4,1,1)}$ et ${\displaystyle (3,3)}$ sont incomparables pour l'ordre de domination alors que la première est lexicographiquement plus grande que la deuxième.
• L'ensemble partiellement ordonné des partitions de ${\displaystyle n}$ est totalement ordonné (et l'ordre de domination et l'ordre lexicographique sont égaux) si et seulement si ${\displaystyle n\leq 5}$. C'est un ensemble partiellement ordonné gradué (possédant une fonction de rang) si et seulement si ${\displaystyle n\leq 6}$.
• Une partition ${\displaystyle p}$ couvre une partition ${\displaystyle q}$ (c'est-à-dire qu'il n'y a pas d'élémentre entre ces deux, formellement ${\displaystyle p\trianglelefteq q}$ et ${\displaystyle p\trianglelefteq r\trianglelefteq q}$ implique ${\displaystyle p=r}$ ou ${\displaystyle q=r}$) si et seulement il existe deux indices ${\displaystyle i,k}$ tels que ${\displaystyle q_{j}=p_{j}}$ pour ${\displaystyle j\neq i,k}$, et ${\displaystyle p_{i}=q_{i+1},p_{k}=q_{k-1}}$; et soit ${\displaystyle k=i+1}$, soit ${\displaystyle q_{k}=q_{i}}$[2].
• Toute partition ${\displaystyle p}$ possède une partition duale ${\displaystyle p^{\star }}$ dont le diagramme de Ferrers est le transposé du diagramme de ${\displaystyle p}$. Cette opération inverse le sens de l'ordre de domination : ${\displaystyle p\trianglelefteq q}$ si et seulement si ${\displaystyle q^{\star }\trianglelefteq p^{\star }.}$

Les partitions d'un entier ${\displaystyle n}$ forment un treillis pour l'ordre de domination. L'opération de conjugaison est un antiautomorphisme de ce treillis. On peut décrire les opérations de treillis comme suit :

À une partition ${\displaystyle p=(p_{1},p_{2},\ldots )}$, complétée éventuellement par des parties nulles, on associe la suite

${\displaystyle {\hat {p}}=(0,p_{1},p_{1}+p_{2},\ldots ,p_{1}+p_{2}+\cdots +p_{n}).}$

On retrouve ${\displaystyle p}$ à partir de ${\displaystyle {\hat {p}}}$ par ${\displaystyle p_{i}={\hat {p}}_{i}-{\hat {p}}_{i-1}.}$. Par exemple, pour (3,1,1,1) et (2,2,2) les suites associées sont (0,3,4,5,6,6,6) et (0,2,4,6,6,6,6). Les suites associées aux partitions sont caractérisées, parmi les suites à ${\displaystyle n+1}$ termes, par les trois propriétés suivantes. Elles sont :

• croissantes au sens large : ${\displaystyle {\hat {p}}_{i}\leq {\hat {p}}_{i+1}~;}$
• concaves : ${\displaystyle 2{\hat {p}}_{i}\geq {\hat {p}}_{i-1}+{\hat {p}}_{i+1}~;}$
• et le premier terme est 0 et le dernier terme est ${\displaystyle n}$ : ${\displaystyle {\hat {p}}_{0}=0,{\hat {p}}_{n}=n.}$

Par la définition de l'ordre de domination, une partition ${\displaystyle p}$ précède une partition ${\displaystyle q}$ ( ${\displaystyle p\trianglelefteq q}$) si et seulement si la suite ${\displaystyle {\hat {p}}}$ est terme par terme inférieure ou égale à ${\displaystyle {\hat {q}}}$. Il en résulte que la borne inférieure ${\displaystyle p\land q}$ de deux partitions ${\displaystyle p}$ et ${\displaystyle q}$ est la partition dont la suite associée est ${\displaystyle \min({\hat {p}}_{i},{\hat {q}}_{i})}$. Ainsi, pour les partitions (3,1,1,1) et (2,2,2), la suite associée à leur borne inférieure est (0,2,4,5,6,6,6), et donc ${\displaystyle p\land q=(2,2,1,1)}$.

Une formule aussi simple n'existe pas pour la borne supérieure parce que le maximum, pris composante par composante, de deux suites concaves n'est plus nécessairement concave: ainsi pour les partitions (3,1,1,1) et (2,2,2) les suites associées sont (0,3,4,5,6,6,6) et (0,2,4,6,6,6,6) et leur maximum, pris terme à terme, est (0,3,4,6,6,6,6) qui n'est pas concave (parce que 2\cdot4<3+6). La construction de la borne supérieure passe par la conjugaison en utilisant l'antiautomorphisme : la borne supérieure ${\displaystyle p\lor q}$ de ${\displaystyle p}$ et ${\displaystyle q}$ est la partition conjuguée de la borne inférieure des conjuguées ${\displaystyle p^{\star }}$ et ${\displaystyle q^{\star }}$ :

${\displaystyle p\lor q=(p^{\star }\land q^{\star })^{\star }.}$

Pour les deux partitions ${\displaystyle p}$ et ${\displaystyle q}$ de l'exemple précédent, leurs partitions conjuguées sont (4,1,1) et (3,3), et leur borne inférieure est (3,2,1). Cette partition est sa propre conjuguée, et la borne supérieure de ${\displaystyle p}$ et ${\displaystyle q}$ est donc (3,2,1). Thomas Brylawski[3] a établi d'autres propriétés du treillis des partitions pour l'ordre de domination. Ainsi, le treillis n'est pas distributif dès que ${\displaystyle n\geq 7}$. En revanche, certaines propriétés des treillis distributifs restent valables dans ce treillis : par exemple, sa fonction de Möbius ne prend que les valeurs 0, 1, et –1.

• Treillis de Young
• Majorisation

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Dominance order » (voir la liste des auteurs).

• (en) Thomas Brylawski, « The lattice of integer partitions », Discrete Mathematics, vol. 6, n^o 3,‎ janvier 1973, p. 201-219 (DOI 10.1016/0012-365X(73)90094-0)
• (en) Ian G. Macdonald, Symmetric functions and Hall polynomials, OUP, coll. « Oxford Mathematical Monographs », 1995, 2^e éd. (ISBN 978-0-19-853489-1, MR 1354144, présentation en ligne)