Opérateur trace
Un opérateur trace est un opérateur mathématique mis en œuvre dans des études d'existence et d'unicité de solutions aux problèmes avec conditions aux limites. L'opérateur trace permet aussi au moyen d'une formulation dans un espace de Sobolev d'étendre au bord d'un domaine la notion de restriction d'une fonction.
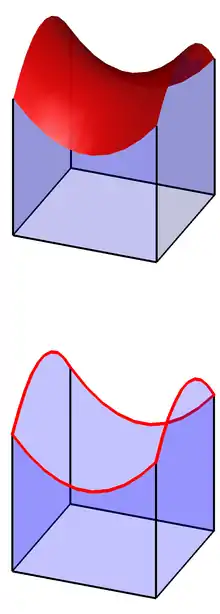
Origine
Soit Ω un ouvert borné de l'espace euclidien ℝn avec une frontière de classe C1[1] ∂Ω. Si u est une fonction C1 (ou simplement continue) sur l'adhérence Ω de Ω, sa restriction est bien définie et continue sur ∂Ω. Si de plus u est la solution d'une équation aux dérivées partielles donnée, elle est en général une formulation faible, qui appartient donc à un certain espace de Sobolev. Les fonctions d'un tel espace ne sont généralement pas continues et sont définies seulement sur Ω (et même seulement à égalité près presque partout), donc leur restriction à ∂Ω n'a aucun sens. Il vient que la restriction simple d'une fonction ne peut pas être utilisée pour définir clairement une solution générale d'une équation aux dérivées partielles avec des conditions aux limites de Ω données.
On peut contourner cette difficulté en considérant que tout élément u d'un espace de Sobolev peut être mal défini en tant que fonction, mais peut toutefois être approché par une suite (un) de fonctions de classe C1 définies sur l'adhérence de Ω. Alors, la restriction u|∂Ω de u sur ∂Ω est définie comme la limite de la suite des restrictions un|∂Ω.
Construction de l'opérateur trace
Afin de définir rigoureusement la notion de restriction d'une fonction dans un espace de Sobolev, soit un réel p ≥ 1. Considérons l'opérateur linéaire
défini sur l'ensemble des fonctions de classe C1 sur Ω à valeurs dans l'espace Lp(∂Ω), vérifiant
Le domaine de T est un sous-ensemble de l'espace de Sobolev W1,p(Ω).
Il existe une constante C, dépendant uniquement de Ω et p, telle que
Alors, comme les fonctions C1 sur Ω sont denses dans W1,p(Ω), l'opérateur T admet un unique prolongement continu (donc, lui aussi, linéaire)
défini sur l'espace entier W1,p(Ω). T est appelé opérateur trace. La restriction (ou trace) u|∂Ω d'une fonction u de W1,p(Ω) est alors donnée par Tu.
Puisque ce prolongement T est séquentiellement continu, pour toute suite (un) de fonctions de classe C1 sur Ω qui converge dans W1,p(Ω) vers u, la suite (un|∂Ω) converge dans Lp(∂Ω) vers Tu.
Application
Considérons la résolution de l'équation de Poisson avec des conditions aux limites de Dirichlet :
Ici, est une fonction continue donnée sur Ω.
Grâce au concept de trace, on définit, dans l'espace de Sobolev H1(Ω) := W1,2(Ω), le sous-espace H1
0(Ω) des fonctions de trace nulle. Alors l'équation admet la formulation faible suivante :
- Trouver telle que
- pour tout dans H1
0(Ω).
Par le théorème de Lax-Milgram, on peut démontrer que ce problème admet une unique solution, et donc que l'équation de Poisson a une solution faible unique.
Un raisonnement similaire peut être utilisé pour prouver l'existence et l'unicité de solutions dans le cas d'autres équations aux dérivées partielles avec des conditions aux limites différentes, telles les conditions de Neumann ou de Robin, la notion de trace étant importante dans ces cas.
Bibliographie
- Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
- (en) Lawrence C. Evans, Partial differential equations, Providence, R.I., AMS, , 2e éd. (1re éd. 1998), 749 p. (ISBN 978-0-8218-4974-3, lire en ligne), p. 174
Notes et références
- Un ouvert Ω de RN est dit de classe C1, si au voisinage de tout point de ∂Ω, il existe un difféomorphisme de classe C1 qui redresse la frontière en un hyperplan de RN−1 et Ω en un des demi-espaces limité par cet hyperplan.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Trace operator » (voir la liste des auteurs).








