Onde équatoriale
Les ondes équatoriales sont des ondulations de la circulation atmosphérique près de l'Équateur. Il s'agit de perturbations faibles de la zone de convergence intertropicale régie par le dégagement de chaleur latente des précipitations convectives associées. En général, elles se propagent vers l'ouest[1]. Ces ondes peuvent se propager normalement tout autour du globe terrestre, tant dans l'horizontal que la verticale, le long de l'équateur météorologique mais s'estompent rapidement quand elles s’en éloignent[2]. En effet, la rotation de la Terre cause l'apparition de la force de Coriolis qui augmente à mesure que l'on s'éloigne de l'Équateur ce qui cause un cisaillement des vents qui étire et dissipe ces ondes.
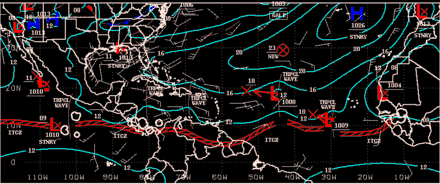
Les ondes équatoriales se retrouvent également dans les courants marins de la même région. Ces ondes atmosphériques et océanographiques jouent un rôle important dans le climat équatorial et dans l'apparition de phénomènes comme le El Niño.
Formation
Plusieurs processus peuvent déclencher des ondes équatoriales. Dans le cas de l'atmosphère, ce sont les processus adiabatiques de formation nuages d'orage dans la zone de convergence intertropicale (ZCIT) qui capturent de l'énergie lors de la montée de l'air en altitude puis la relâchent ailleurs lors de la formation du nuage et des pluies abondantes qui lui sont associées. La différence de chaleur entre deux endroits dans la ZCIT causent alors une variation de l'écoulement[2]. Dans l'océan, ce sont les changements de directions des alizés qui les causent[2].
Les ondes équatoriales peuvent être séparées en différents types, selon les forces dynamiques qui les causent. Ces types ont des périodes et des directions de propagation différentes. Les ondes les plus courtes sont les ondes de gravité équatoriales alors que les plus longues sont celles de Rossby. Entre les deux, on retrouve les ondes de Kelvin équatoriales[2].
Ondes de Rossby et de gravité
La vitesse de propagation des ondes peut être calculée quand on considère l'écoulement d'un fluide non visqueux dans une couche d'épaisseur uniforme H. Parce que le paramètre « f » de la force de Coriolis (f= 2Ω sin(θ) où Ω est le moment angulaire de la Terre, 7,2921 10−5 rad/s, et θ est la latitude) est zéro près de l'Équateur, il faut faire une approximation[2]. Celle-ci se nomme approximation du plan Beta (β) où f est estimé par βy où β est la variation de f avec la distance à l'Équateur () et y est la distance de l'Équateur [2].
Le calcul néglige la friction et utilise cette approximation[2] - [3] :
- Avec l'équation de continuité, qui tient compte des effets de convergence et de divergence horizontales de l'air, on obtient une variation du géopotentiel (Φ) avec le temps de :
- La composante est-ouest u dit zonale du vent est :
- La composante nord-sud v du vent est :
La solution de ces trois équations à trois inconnues donne une solution exponentielle de la forme :
En utilisant le terme ω pour remplacer la fréquence angulaire, on obtient trois solutions pour les vitesses de déplacements horizontales, verticales et latitudinaires. Celles-ci correspondent au déplacement des ondes de Rossby, de gravité et mixtes gravité-Rossby[2]. Les ondes de gravité peuvent se déplacer vers l'est ou l'ouest. Les ondes de gravité-Rossby, observées pour la première dans la stratosphère le chercheur japonais M. Yanai en 1966, transporte toujours l'énergie produite vers l'est mais le déplacement des crêtes et des creux peut être vers l'ouest si la période de l'onde est assez longue, la vitesse de groupe et la vitesse de phase pouvant être de directions différentes[4].
Ondes de Kelvin équatoriales
C'est Lord Kelvin qui a le premier remarqué des ondes se propageant le long des côtes mais se dissipant si on s'en éloigne. Ces ondes de Kelvin se propagent vers la droite dans l'hémisphère nord et la gauche dans celui du sud. Les ondes équatoriales de Kelvin suivent la même règle et se comportent un peu comme si l'Équateur était un mur et vont se déplacer vers l'est de chaque côté de celui-ci[2].
Les équations utilisées pour trouver le mouvement de ces ondes sont les mêmes qu'antérieurement sauf qu'il n'y a pas de mouvement méridional () dans ce cas (aucun mouvement nord-sud) :
- Avec l'équation de continuité, qui tient compte des effets de convergence et de divergence horizontales de l'air, on obtient une variation du géopotentiel avec le temps de[2] :
- La composante zonale du vent est :
- La composante nord-sud du vent est :
La solution de ces équations donne une vitesse de phase de : c2 = gH, la même solution que pour une onde de gravité dans un fluide peu profond sans les effets de la rotation de la Terre[2]. Ces ondes sont en conséquence non dispersives, parce que la vitesse de phase est indépendante du nombre d'onde. Elles se propagent uniquement vers l'est parce que lorsque Φ tend vers zéro, y tend vers l'infini[3].
Relation avec ENSO
Plusieurs chercheurs ont utilisé des modèles numériques qui couplent les interactions atmosphère-océan pour simuler l'oscillation australe. Ils ont trouvé qu'une oscillation de Madden-Julian (OJM), un cycle de 30 à 60 jours dans le passage des systèmes météorologiques équatoriaux, peuvent déclencher des ondes de Kelvin océaniques grâce à l'intense relâchement de chaleur latente. Les ondes de Kelvin équatoriales peuvent ensuite déclencher le phénomène El Niño[5].
Notes et références
- Organisation météorologique mondiale, « Onde équatoriale », Glossaire de la météorologie, Eumetcal (consulté le )
- (en) James R. Holton, An Introduction to Dynamic Meteorology, Burlington, MA, Elsevier Academic Press, , 4e éd., 535 p. (ISBN 978-0-12-354015-7 et 0123540151, présentation en ligne, lire en ligne), p. 394–400
- (en) Dalin Zhang, Waves in Rotating, Homogeneous Fluids, College Park, Université du Maryland, , Personal communication
- M. Yanai et T. Maruyama, « Stratospheric wave disturbances propagating over the equatorial Pacific », Journal of the Atmospheric Sciences, American Meteorological Society, vol. 29, no 2, , p. 368-375 (lire en ligne)
- (en) « El Nino and La Nina », Stormsurf, (consulté le )
Voir aussi
Articles connexes
Lien externe
- (en) David S. Battisti et Michela Biasutti, « Developing a Theory for ENSO (Développement d'une théorie de l'ENSO) », UCAR (consulté le )









