Noyau de système d'exploitation formellement prouvé
Un noyau de système d'exploitation formellement prouvé (ou Formal Verification of an OS Kernel, le terme anglophone) est un noyau pour lequel on a prouvé de façon mathématique que celui-ci ne possédait aucun défaut de conception. Cette vérification dite « formelle » est définie en fonction de plusieurs critères appelés critères communs.
L’idée de la vérification formelle des systèmes d'exploitation apparaît dans les années 1970. En effet, les programmes informatiques étant convertibles mathématiquement, l’envie de prouver qu’ils sont corrects est automatiquement apparue. Et cela est fait de manière formelle afin que cela puisse être vérifié/ checké par une machine.
Plusieurs méthodes existent afin de prouver formellement que ces noyaux sont sans erreur, telles que la Vérification de modèles ou la Démonstration automatique de théorèmes. Mais ces méthodes seules ne suffisent pas, des outils de vérification viennent les compléter : on parle d’outils comme Spin ou ComFoRT qui sont des models checkeurs ou alors via des langages formels comme Haskell ou Coq. Via ces méthodes et ces outils, différents critères doivent être respectés. En fonction du nombre de critères validés, un niveau d’assurance est donné au noyau. Plus le niveau est élevé, plus le noyau est garanti.
Historiquement, le premier système d'exploitation formellement prouvé est le sel4. Ce projet a été complété en 2009. Il s’agit d’un micronoyau de la famille L4 conçu pour offrir des mécanismes de sécurité forts tout en conservant la haute performance.
Le fait de prouver qu’un système d'exploitation est formellement correct est une preuve de fiabilité : cela prouve que son noyau peut résister à tout type de situation. C’est aussi une preuve de sécurité.
Mais il est à noter que la vérification formelle d’un système d'exploitation est encore en développement et comporte actuellement en 2016 des nombreuses lacunes : on prouve qu’un système d'exploitation est fonctionnellement correct, pas qu’il soit parfait notamment au niveau de la sécurité.
Généralités
Système d'exploitation
Prouver formellement qu’un système d'exploitation est sécurisé et sans failles est un sujet de recherche de plus de 30 ans[1]. En effet, on ne peut être assuré de la sécurité et la fiabilité d’un système informatique uniquement si son système d'exploitation est garantie sans erreur. Il est à noter que le noyau qui est exécuté dans le mode le plus privilégié dans le processeur, à des accès illimités au matériel. Par conséquent, la moindre erreur dans le noyau de l’OS peut compromettre toute la légitimité du reste du système.
Un système d'exploitation, au même titre que n’importe quel code informatique, peut-être converti mathématiquement, et donc, si l’on souhaite s’assurer que celui-ci est sans erreur, il suffit de le prouver.
Il est possible de pousser la robustesse et la sécurité au point de garantir l’absence de bugs ainsi que la présence de très hautes propriétés de sécurités, mais cela avec de très petits noyaux. En effet, il est inévitable d’avoir des erreurs dans un code informatique, par conséquent plus la taille du code est élevée, plus la possibilité d’avoir des erreurs est grande. Évidemment, la réduction parfois radicale de la taille des systèmes d'exploitation peut amener à une forte augmentation de la complexité ainsi qu’à une baisse des performances et des fonctionnalités.
Objectifs de la preuve
Il y a deux aspects d'un noyau que l'on peut souhaiter vérifier.
Le premier aspect est la sécurité du noyau. Celle-ci comprend la confidentialité des informations auxquelles le noyau a accès, ainsi que l'intégrité du noyau, où quel code peut être exécuté et ce qu'il peut réaliser.
Le second aspect concerne la sûreté du noyau. Pour des applications critiques où la sécurité d'usagers peut être en jeu, comme dans l'aéronautique, il est vital de garantir certaines propriétés. Ces propriétés peuvent être le respect de contraintes temporelles comme un temps de réaction limite à un événement extérieur[2].
Méthodes de vérifications
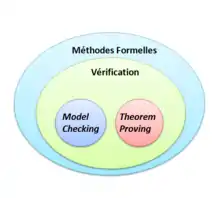
Vérification de modèles
Il faut tout d'abord noter que la Vérification de modèles ne travaille pas directement sur le noyau du système d'exploitation. Dans un premier temps, il faut formaliser le noyau sous forme de modèle. En effet, le but de la Vérification de modèles va être d'explorer de manière exhaustive ce modèle afin de vérifier que le noyau supporte n'importe quel état qui peut se présenter. C'est-à-dire, peu importe l'erreur qui va survenir, cela ne fera pas planter l'OS.
De ce fait, Vérification de modèles n'est pas une méthode qui pourra être efficace sur des noyaux d'OS modernes vu qu'ils sont assez volumineux en taille : cela prend énormément de temps. On va plutôt l'utiliser sur des noyaux de petite taille, essentiellement des micronoyaux.
On va plutôt utiliser cette méthode pour vérifier certaines règles de sécurité ou bien des propriétés bien précises. De plus, vu qu'il a fallu transposer le noyau sous forme de modèle, ce qui est fait généralement fait manuellement, cela prend du temps et est sujet à erreurs.
Certains outils comme SLAM, peuvent travailler directement sur le noyau, mais ils ne peuvent vérifier que de simples propriétés, or cela n'est pas suffisant pour prouver que le système est correct.
En conséquence, Vérification de modèles n'est pas une méthode qui est souvent utilisée.
Theorem proving
Contrairement à la Vérification de modèles, le but de theorem proving va être d'exprimer les propriétés du noyau et son modèle de façon logique. Ensuite, on va en déduire une preuve mathématique et vérifier qu'elle confirme ces propriétés.
Cette méthode a de grands avantages par rapport à la Vérification de modèles :
- La taille du noyau ne compte pas vu qu'une preuve mathématique peut gérer de très grands nombres. On peut donc appliquer cette méthode sur tous types d'OS : en particulier les plus complexes et les plus fonctionnels.
- Via cette méthode, la vérification des preuves mathématiques peut se faire de manière automatique : peu importe que cette preuve soit compliquée à résoudre pour un humain, un model checker peut le faire sans soucis.
À noter que comparée à la Vérification de modèles, cette méthode requiert plus d'interaction humaine, mais cela peut justement être sa force : cela permet de savoir que le système est correct mais aussi pourquoi.
Preuve par le code
La preuve par le code (en) (en anglais, PCC pour Proof-carrying code), est un framework pour les mécanismes de vérification des langages de programmation.
Dans la même logique que le theorem proving, la PCC créée et vérifie une preuve mathématique mais à partir du langage de programmation lui-même.
Se trouve deux types de PCC :
- PCC conventionnel
- PCC fondationnel
Le point négatif de cette méthode est qu'il ne doit pas y avoir d'erreurs dans l'outil de vérification.
Critères communs
Les critères communs (CC ou Common Criteria for Information Technology Security Evaluation, version anglophone) sont reconnus mondialement comme un standard pour la sécurité informatique depuis 1999[3], et cela a attisé l’intérêt des chercheurs pour les méthodes formelles ces dernières années.
Ils remplacent les standards précédents : ITSEC (Europe) et TCSEC (États-Unis). Ils sont reconnus par 24 pays et administrés par les autorités locales de ces pays.
Au niveau de la validation, les CC sont plus orienté produit et moins orientées procédures que les anciens standards. Ils distinguent les responsabilités des développeurs de celle des évaluateurs[4]. Cela dit, ils représentent une forte avancée vers la sécurité des produits informatiques.
Il y a 7 niveaux d'évaluations (EALs ou Evaluation Assurance Levels, version anglophone) dans les CC ou le niveau 7 est le plus élevé. Ces niveaux définissent un niveau de qualité des produits, mais surtout assure une très forte rigueur dans la mise en place des mesures de sécurité des produits informatiques.
En ce qui concerne les noyaux d'OS, le niveau de sécurité le plus haut atteint est le niveau 6, la majorité atteint généralement le niveau 4. À noter que le nombre de noyaux ayant atteint ce niveau est extrêmement faible. Parmi eux, nous allons trouver :
| Nom OS | Niveau CC | Année |
|---|---|---|
| Mac OS X | 3 | 2005 |
| Windows 2008 Server | 4 | 2009 |
| Novell SUSE Linux Enterprise Server | 4 | (?) |
| Oracle Solaris | 4 | (?) |
| Red Hat Enterprise Linux 5 | 4 | 2007 |
| Red Hat Enterprise Linux 6 | 4 | 2014 |
| Green Hills INTEGRITY-178B | 6 | 2008 |
Cependant, bien que les méthodes de vérification formelles assurent une haute fiabilité, une vérification au niveau du code n'est pas requise par les critères communs[4].
De plus, les critères communs sont considérés consommé étant trop coûteux, produisent trop de paperasse et adhèrent à un modèle de procès légal
Outils de vérifications
Langages formels
Les outils de preuve formelle mécanisée (vérifiée par ordinateur) ne sont pas encore aussi pratiques à utiliser qu'ils le pourraient, donc faire une preuve formelle complète c'est un travail très important. Coq est un outil basé sur l'idée qu'un système de typage suffisamment puissant peut aussi devenir un système de preuve. On peut donc écrire des preuves et des programmes dans un même langage (mais est donc très contraignant pour la programmation), et il y a aussi un langage spécialisé pour écrire des preuves automatisées, c'est-à-dire en fait écrire un petit programme qui trouve tout seul la preuve, au lieu de construire directement l'arbre de preuve[5].
Il existe d'autres outils de preuve formelle, Twelf en particulier est réputé pour être un peu plus facile à utiliser (et, en contrepartie, un peu plus restreint et moins généraliste).
Haskell est un outil pour développer simultanément une spécification du noyau et une implémentation de référence pour l'évaluation et le test. La mise en œuvre peut être utilisée en conjonction avec un simulateur pour exécuter un binaire d'application réelles, tandis que la spécification génère une entrée à un probateur de théorème interactif pour la preuve formelle de propriétés. La spécification Haskell sert de support pour le prototypage itératif de la mise en œuvre ainsi que pour le modèle de système pour les équipes de modélisation de noyau et formelles, c'est-à-dire que la spécification Haskell forme un pont entre les équipes améliorant le flux d'idées, avec une faible barrière d'entrée pour les deux. De plus, l'implémentation de référence, lorsqu'elle est couplée à un simulateur, peut être utilisée pour exécuter des binaires natifs[6].
Vérification de modèles
ImProve est un langage impératif simple avec des affectations variables et des énoncés conditionnels. Les assertions ImProve sont vérifiées formellement en utilisant la vérification de modèle SMT. Pour la mise en œuvre et la simulation du système, ImProve compile vers C, Ada, Simulink et Modelica. TLC est un outil adapté pour la spécification de réactif systèmes. Le comportement d'un réactif système est décrit par une spécification formelle, et les propriétés, sont exprimées par TLC[7].
Exemple d'OS formellement prouvés
SeL4
Il fait partie de la famille des micronoyaux. Il adopte une approche de partitionnement qui fournit une forte isolation totale d’applications. Il a subi la Worst Case Execution Time, cette dernière devenue indispensable dans la vérification des systèmes, a essayé de tester les limites du Sel4[8].
Le Sel4 comporte 10 000 lignes de code, exécutable sur différentes plateformes : X86 et ARM. L' avantage du Sel4 est qu’il fournit le partitionnement nécessaire pour soutenir des logiciels mixtes[9].
Intérêts de la vérification formelle d'OS
Sécurité
La sécurité et la fiabilité d'un système informatique ne peuvent être aussi bonne que celle du système d'exploitation (OS). Le noyau, défini comme la partie du système s'exécutant dans les zones les plus profondes du processeur, dispose d'un accès illimité au matériel.
Par conséquent, tout défaut dans la mise en œuvre du noyau risque de compromettre le bon fonctionnement du reste du système.
Il est évidemment inévitable d'avoir des bogues dans un code important. En conséquence, lorsque la sécurité ou la fiabilité est primordiale, l'approche habituelle est de réduire la quantité de code privilégié, afin de minimiser l'exposition aux bugs. C'est l'une des principales motivations derrière les noyaux de sécurité et les noyaux de séparation, l'approche MILS, les microkernels et les kernels d'isolement, l'utilisation de petits hyperviseurs comme base de confiance minimale, ainsi que les systèmes qui exigent l'utilisation de langage de type sécurisé Tous les codes, à l'exception d'un noyau sale. De même, le critère commun au niveau d'évaluation le plus strict exige que le système sous évaluation ait une conception simple.
Avec des noyaux vraiment petits, il devient possible de renforcer la sécurité et la robustesse, au point où il est possible de garantir l'absence de bugs. Ceci peut être réalisé par une vérification formelle vérifiée par machine, fournissant une preuve mathématique que la mise en œuvre du noyau est conforme à sa spécification et exempte de défauts de mise en œuvre induits par le programmeur.
seL4 est le tout premier noyau OS à finalité générale qui est entièrement vérifié pour la correction fonctionnelle. En tant que tel, c'est une plate-forme de fiabilité sans précédent, qui permettra la construction de systèmes hautement sécurisés et fiables sur le dessus.
La propriété fonctionnelle correcte que nous prouvons pour seL4 est beaucoup plus forte et plus précise que ce que les techniques automatisées telles que la vérification de modèles, l'analyse statique ou les implémentations du noyau dans des langages de type sécurité peuvent atteindre. Nous analysons non seulement les aspects spécifiques du noyau, tels que l'exécution sûre, mais aussi fournir une spécification complète et la preuve du comportement précis du noyau[10].
Limites de la preuve
Il y a cependant une limite à la portée de la preuve d'un noyau. La preuve de l'"exactitude" d'un noyau est valide si les axiomes sur lesquels elle repose sont valides.
Parmi ces axiomes, il peut y avoir le bon fonctionnement du matériel qui exécutera le noyau[11].
Une possibilité est alors d'exécuter le noyau sur un matériel qui ne valide pas les axiomes sur lesquels a été fondée la preuve pour tenter d'attaquer le noyau. Il est aussi possible de provoquer des fautes dans celui-ci, par exemple en causant une surchauffe, et d'en extraire des informations. Un dernier exemple serait d'exploiter des spécificités du matériel qui n'ont pas été couvertes par la preuve pour permettre des attaques par canaux auxiliaires. Un exemple serait que les timings du matériel ne soient pas considérés dans la vérification et que celle-ci ne puisse garantir l'absence de canal caché, qui pourrait permettre de véhiculer des informations.
La compréhension de la spécification du noyau peut également être attaquée. Cela peut mettre en évidence des comportements du noyau qui n'avaient pas été interprétés.
Coûts
Un aspect évident de la vérification est le coût de la preuve, cela dépend évidemment la nature du changement, en particulier la quantité de code qu'il modifie, le nombre d'invariants qu'il applique et son degré de localisation[12].
Depuis les premières tentatives de vérification du noyau, il y a eu des améliorations spectaculaires dans la puissance des outils de démonstration de théorèmes disponibles. Des assistants de vérification comme ACL2 (en), Coq, PVS, HOL et Isabelle ont été utilisés dans un certain nombre de vérifications réussies, allant des mathématiques et des logiques aux microprocesseurs, aux compilateurs et aux plateformes de programmation complètes comme JavaCard.
Cela a entraîné une réduction significative du coût de la vérification formelle et une diminution du seuil de faisabilité. En même temps, les avantages potentiels se sont accrus, donnés par exemple le déploiement accru de systèmes embarqués dans des situations critiques ou de vie ou les énormes enjeux créés par la nécessité de protéger les droits de propriété intellectuelle évalués à des milliards[13].
Historique
| Années | Projet | Plus haut niveau | Plus bas niveau | Specs | Preuves | Outils de vérification | Approche |
|---|---|---|---|---|---|---|---|
| (?) - 1980 | UCLA Secure Unix | Modèle de sécurité | Pascal | 20% | 20% | XIVIUS | Alphard |
| 1973 – 1983 | PSDOS | Niveau application | Code source | 17 couches | 0% | SPECIAL | HDM |
| (?) - 1987 | KIT | Tâches isolés | Assembleur | 100% | 100% | Boyer Moore | Equivalence d’interpreteur |
| 2001 – 2008 | VFiasco/Rodin | Ne crash pas | C++ | 70% | 0% | PVS | Compilateur sémantique |
| 2004 – (?) | EROS/Coyotos | Modèle de sécurité | BitC | Modèle de sécurité | 0% | ACL2 | Basé sur le langage |
| 2004 - (2008) | Verisoft | Niveau application | Gate level | 100% | 75% | Isabelle | Complètement persuasif |
| 2005 – (2008) | L4.SeL4 | Modèle de sécurité | C/Assembleur | 100% | 70% | Isabelle | Performances, production de code |
Bibliographie
- (en) Thomas Hallgren, Jones Mark P, Rebekah Leslie et Andrew Tolmach, « A principled approach to operating system construction in Haskell », ACM, vol. Volume 40, , p. 116-128 (ISBN 1-59593-064-7, DOI 10.1145/1090189.1086380)
- (en) Harvey Tuch, Gerwin Klein et Gernot Heiser, « OS Verification -- Now! », usenix, vol. Volume 10, , p. 2-2 (lire en ligne)
- (en) Gerwin Klein, Kevin Elphinstone et Gernot Heiser, « seL4: formal verification of an OS kernel », ACM, , p. 207-220 (ISBN 978-1-60558-752-3, DOI 10.1145/1629575.1629596)
- (en) Bernard Blackham, Yao ShiShi et Sudipta Chattopadhyay, « Timing Analysis of a Protected Operating System Kernel », IEEE, , p. 1052-8725 (ISSN 1052-8725, DOI 10.1109/RTSS.2011.38)
- (en) Chuchang Liu et Mehmet.A Orgunb, Verification of reactive systems using temporal logic with clocks, , 1-32 p. (DOI 10.1016/S0304-3975(99)00008-0)
- (en) Kevin Elphinstone1, Gerwin Klein, Philip Derrin, Timothy Roscoe2 et Gernot Heiser, « Towards a Practical, Verified Kernel », usenix.org, (lire en ligne)
- (en) Freek Wiedijk, « Comparing mathematical provers », usenix.org, (ligne=http://cs.ru.nl/~freek/comparison/diffs.pdf)
- (en) T. Vickers Benzel, « Analysis of a Kemel Verification », IEEE Symposium, , p. 125-125 (ISSN 1540-7993, DOI 10.1109/SP.1984.10015)Security and Privacy, 1984 IEEE Symposium on
- (en) O. Ganea, F. Pop, C. Dobre et V. Cristea, « Specification and Validation of a Real-Time Simple Parallel Kernel for Dependable Distributed Systems », EIDWT, , p. 320-325 (ISBN 978-1-4673-1986-7, DOI 10.1109/EIDWT.2012.48)Emerging Intelligent Data and Web Technologies (EIDWT), 2012 Third International Conference on
- (en) J. Gorski et A. Wardzinski, « Formal specification and verification of a real-time kernel », Euromicro, , p. 205-211 (ISBN 0-8186-6340-5, DOI 10.1109/EMWRTS.1994.336841)Real-Time Systems, 1994. Proceedings., Sixth Euromicro Workshop on
- (en) G. Naeser et K. Lundqvist, « Component-based approach to run-time kernel specification and verification », Euromicro, , p. 68-76 (ISSN 1068-3070, DOI 10.1109/ECRTS.2005.11)Real-Time Systems, 2005. (ECRTS 2005). Proceedings. 17th Euromicro Conference on
- (en) B. L. Di Vito, P. H. Palmquist, E. R. Anderson et M. L. Johnston, « Specification and verification of the ASOS kernel », IEEE Computer Society Symposium, , p. 61-74 (ISBN 0-8186-2060-9, DOI 10.1109/RISP.1990.63839)Research in Security and Privacy, 1990. Proceedings., 1990 IEEE Computer Society Symposium on
- (en) R. M. Tol, « A small real-time kernel proven correct », Real-Time Systems Symposium, , p. 227-230 (ISBN 0-8186-3195-3, DOI 10.1109/REAL.1992.242659)Real-Time Systems Symposium, 1992
- (en) T. Murray, D. Matichuk, M. Brassil, P. Gammie, T. Bourke, S. Seefried, X. Gao et G. Klein, « seL4: From General Purpose to a Proof of Information Flow Enforcement », IEEE Symposium, , p. 415-429 (ISSN 1081-6011, DOI 10.1109/SP.2013.35)Security and Privacy (SP), 2013 IEEE Symposium on
- (en) G. Klein, J. Andronick, K. Elphinstone, T. Murray, T. Sewell, R. Kolanski et G. Heiser, « Comprehensive Formal Verification of an OS Microkernel », ACM Trans. Comput. Syst., , p. 70 (DOI 10.1145/2560537)
- (en) Y. Zhang, Y. Dong, H. Hong et F Zhang, « Code Formal Verification of Operation System », I.J.Computer Network and Information Security,
- (en) A. W. Appel, « Foundational proof-carrying code », Logic in Computer Science, , p. 25-34 (ISSN 1043-6871, DOI 10.1109/FITS.2003.1264926)Logic in Computer Science, 2001. Proceedings. 16th Annual IEEE Symposium on
- (en) Gernot Heiser, Toby Murray et Gerwin Klein, « It's Time for Trustworthy Systems », IEEE Computer Society, , p. 67-70 (ISSN 1540-7993, DOI 10.1109/MSP.2012.41)Secure Syst. Group, IBM Res. Div. Zurich
- (en) Steven H. VanderLeest, « The open source, formally-proven seL4 microkernel : considerations for use in avionics », IEEE Computer Society, (ISSN 2155-7209, DOI 10.1109/MSP.2012.41, lire en ligne)conférence
- (en) Gerwin Klein, Kevin Elphinstone, Gernot Heiser, June Andronick, David Cock, Philip Derrin, Dhammika Elkaduwe, Kai Engelhardt, Rafal Kolanski, Michael Norrish, Thomas Sewell, Harvey Tuch et Simon Winwood, « seL4: formal verification of an OS kernel », ACM digital library, , p. 207-220 (ISBN 978-1-60558-752-3, DOI 10.1145/1629575.1629596)
- (en) Bernard Beckert, Daniel Bruns et Sarah Grebing, « Mind the Gap: Formal Verification and the Common Criteria (Discussion Paper) », EasyChair, vol. 3, , p. 4-12 (ISSN 2398-7340, lire en ligne)
- (en) Gerwin Klein, « Correct OS kernel? Proof? done! », Usenix.org, vol. 34, (lire en ligne)
Notes et références
- Klein 2009
- Heiser 2012, p. 68
- Beckert 2012, p. 4
- Beckert 2012, p. 5
- Freek Wiedijk 2003, p. 9,10
- Hallgren 2005, p. 1
- Liu 1999, p. 1
- Gernot 2012, p. 67,70
- VanderLeest 2016
- Gerwin 2009, p. 1,3
- Heiser 2012, p. 69
- Gerwin Klein 2009, p. 13
- Harvey Tuch 2005, p. 12,15