Nombre semi-parfait
En mathématiques, un nombre semi-parfait ou nombre pseudoparfait est un entier naturel n qui est égal à la somme de certains ou de tous ses diviseurs stricts.
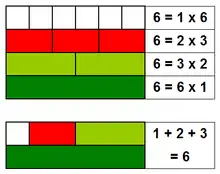
6 est un nombre semi-parfait, car il est égal à la somme de 1, 2 et 3 qui sont tous des diviseurs stricts de 6.
Les premiers nombres semi-parfaits sont 6, 12, 18, 20, 24, 28, 30, 36, 40… (suite A005835 de l'OEIS) ; chaque multiple d'un nombre semi-parfait est semi-parfait, et chaque nombre de la forme 2mp pour un entier naturel m et un nombre premier p tels que p < 2m+1 est aussi semi-parfait.
Un nombre semi-parfait qui est égal à la somme de tous ses diviseurs stricts est appelé un nombre parfait ; un nombre abondant qui n'est pas semi-parfait est appelé un nombre étrange.
Voir aussi
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Semiperfect number » (voir la liste des auteurs).
Articles connexes
Lien externe
(en) Eric W. Weisstein, « Semiperfect Number », sur MathWorld
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.