Nombre hexagonal centré

En mathématiques, un nombre hexagonal centré est un nombre figuré polygonal centré qui peut être représenté par un hexagone régulier ayant un point en son centre et tous ses autres points disposés en couches hexagonales concentriques de 6 points, 12 points, 18 points, etc.

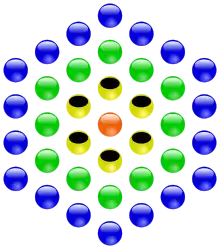
Représentation du 4-ième nombre hexagonal centré

Les quatre plus petits nombres hexagonaux centrés sont : ${\begin{aligned}&C_{6,1}={\color {red}1},\\&C_{6,2}=1+{\color {orange}6}=7,\\&C_{6,3}=7+{\color {green}12}=19,\\&C_{6,4}=19+{\color {blue}18}=37.\end{aligned}}$

Gnomon, relation de récurrence

Pour tout entier $n$ ≥ 1, le $n$ -ième hexagone centré a un point central et $n$ – 1 couches hexagonales régulières. Ainsi, il comporte $n$ points sur chaque rayon et sur chaque côté.

Pour tout entier $n$ ≥ 2, la dernière couche du $n$ -ième hexagone centré comporte 6( $n$ – 1) points ; c'est le gnomon associé au ( $n$ – 1)-ième hexagone centré, et faisant passer au $n$ -ième : $\forall \ n\geq 2,\ C_{6,n}=C_{6,n-1}+6(n-1).$

Le $n$ -ième nombre hexagonal centré s'obtient donc en ajoutant 1 au produit par 6 du ( $n$ – 1)-ième nombre triangulaire : $C_{6,n}=1+6\,{\frac {n(n-1)}{2}}=1+6T_{n-1}$ .

Exemple

Représentation à la fois du 5-ième nombre hexagonal centré et des six 4-ièmes nombres triangulaires autour de son centre

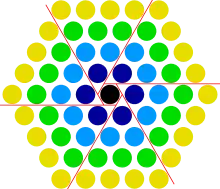
Le 5-ième nombre hexagonal centré est 1 plus 6 fois le 4-ième nombre triangulaire : ${\begin{aligned}C_{6,5}&={\color {red}1}+{\color {orange}6}+{\color {green}12}+{\color {blue}18}+{\color {purple}24}\\&={\color {red}1}+6({\color {orange}1}+{\color {green}2}+{\color {blue}3}+{\color {purple}4})\\&={\color {red}1}+6T_{4}\\&={\color {red}1}+6\times 10\\&=61.\end{aligned}}$

Applications pratiques

Les nombres hexagonaux centrés ont des applications pratiques dans les domaines de la gestion de production et de la logistique, par exemple l'empaquetage de certains produits dans de plus grands récipients circulaires, comme les saucisses de Francfort dans des conteneurs cylindriques.

Liste de nombres hexagonaux centrés, propriété de congruence

Les dix plus petits nombres hexagonaux centrés sont 1, 7, 19, 37, 61, 91, 127, 169 et 217 (voir la suite A003215 de l'OEIS).

Le chiffre des unités en base dix de cette suite d'entiers suit le motif 1-7-9-7-1 ; les nombres hexagonaux centrés sont donc tous impairs.

Liens avec d'autres nombres figurés

Pour trouver les nombres hexagonaux centrés qui sont aussi des nombres triangulaires ou des nombres carrés, ou tout cela à la fois, il suffit de résoudre les équations de Pell-Fermat associées.

Nombre hexagonal centré triangulaire

$C_{6,n}=T_{m}\Leftrightarrow (2m+1)^{2}-6(2n-1)^{2}=3$ . Les trois plus petits nombres à la fois hexagonaux centrés et triangulaires sont donc $C 6, 1$ = 1 = $T 1$ , $C 6, 6$ = 91 = $T 13$ et $C 6, 55$ = 8 911 = $T 133$ (pour les suivants, voir la suite A006244).

Nombre hexagonal centré carré

$C_{6,n}=m^{2}\Leftrightarrow (2m)^{2}-3(2n-1)^{2}=1$ . Les trois plus petits nombres à la fois hexagonaux centrés et carrés sont donc $C 6, 1$ = 1 = 1², $C 6, 8$ = 169 = 13² et $C 6, 105$ = 32 761 = 181² (pour les suivants, voir la suite A006051).

Liens avec à la fois les nombres triangulaires et les nombres carrés

1 est le seul nombre à la fois hexagonal centré et carré triangulaire[1].
Pour tout entier $n$ ≥ 1, la différence entre le $n$ -ième nombre carré impair et le $n$ -ième nombre hexagonal centré est le ( $n$ – 1)-ième nombre oblong :

n

– 1)² – [1 + 3

n

(

n

– 1)] =

n

(

n

– 1).

Autrement dit, le

n

-ième nombre carré impair est la somme du

n

-ième nombre hexagonal centré et du double du (

n

– 1)-ième nombre triangulaire :

(2 n - 1) 2

C 6, n

2 T n -1

Cette relation peut faire l'objet d'une preuve sans mot : placer les deux triangles (ayant

n

– 1 points sur chaque côté) contre deux côtés opposés (ayant

n

points chacun) de l'hexagone forme deux pointes opposées et le corps d'un losange (ayant 2

n

– 1 points sur chaque côté).

Somme partielle de nombres hexagonaux centrés : nombre cubique

Pour tout entier $n$ ≥ 1, le $n$ -ième nombre hexagonal centré $C 6, n$ est le gnomon $n$ ³ – ( $n$ – 1)³[1].

(En particulier, les nombres à la fois hexagonaux centrés et premiers sont les nombres premiers différences de deux cubes consécutifs, c'est-à-dire les nombres premiers cubains[1] de première espèce.)

Donc[1] la somme des $n$ plus petits nombres hexagonaux centrés est $n$ ³. Ainsi, les nombres pyramidaux hexagonaux centrés sont simplement les nombres cubiques[2], mais représentés par des formes différentes.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Centered hexagonal number » (voir la liste des auteurs).

(en) Eric W. Weisstein, « Hex Number », sur MathWorld.
(en) Eric W. Weisstein, « Hex Pyramidal Number », sur MathWorld.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.