Méthode de Debye-Scherrer

La méthode de Debye-Scherrer consiste à sonder un échantillon cristallin poudreux en dirigeant sur celui-ci un faisceau monochromatique de rayons X. Les microcristaux, dont la taille peut varier entre 0,01 et 0,001 mm, sont orientés de façon aléatoire à l’intérieur de l’échantillon et, pour un échantillon contenant entre ${\displaystyle 10^{7}}$ et ${\displaystyle 10^{13}}$ microcristaux, il en existe toujours une grande quantité pour lesquels l’orientation des plans réticulaires avec l’angle d’incidence ${\displaystyle \theta }$ du faisceau satisfait la loi de Bragg[2] :

${\displaystyle 2d\sin \theta =n\cdot \lambda }$

où :

• d est la distance interréticulaire, soit la distance entre deux plans de la même famille {hkl}
• n est l’ordre de diffraction (nombre entier)
• ${\displaystyle \theta }$ est le demi-angle de diffraction,
• ${\displaystyle \lambda }$ est la longueur d’onde du faisceau de rayons X

Ainsi, chaque microcristal orienté favorablement créera un rayon diffracté formant un angle de ${\displaystyle 2\theta }$ avec l’axe d’émission du faisceau incident. L’ensemble des faisceaux réfléchis pour une même distance interréticulaire à l’intérieur des différents microcristaux formera alors un cône d’ouverture ${\displaystyle 2\theta }$ centré sur le faisceau de rayons X d’origine.

Représentation des anneaux de diffraction

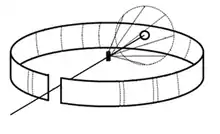
L’intersection de ces cônes de diffraction avec un film plan déposé circulairement aux alentours de l’échantillon créera des anneaux circulaires centrés sur les orifices d’entrée et de sortie du faisceau incident. Par contre, si le nombre de microcristaux à l’intérieur de l’échantillon est insuffisant, les anneaux de diffraction apparaîtront comme une série de points placés circulairement[2]. Puisque chaque cône de diffraction est imputable à une distance interréticulaire ${\displaystyle d_{hkl}}$ précise, l’étude de la distance angulaire séparant deux anneaux diffractés sur le film permet alors de définir :

• la distance interréticulaire entre les plans ayant créé un anneau en particulier
• les indices de Miller (hkl) du plan étudié
• les paramètres de maille du matériau

Il est important de souligner que les deux derniers paramètres mentionnés ci-haut ne peuvent être obtenus à l’aide de la méthode de Debye-Scherrer que si l’on connaît déjà le système cristallin de la poudre étudiée.

Techniquement, la méthode pourrait aussi servir à obtenir de l’information sur la taille des grains à l’intérieur de la poudre, inversement proportionnelle à la largeur des anneaux, ainsi que sur l’intensité du faisceau diffracté qui correspond à la teinte des anneaux[3]. Toutefois, l’incertitude sur les mesures nécessaires à l’évaluation de ces deux paramètres est si importante face à celle qui est obtenue avec les diffractomètres automatisés que la méthode de Debye-Scherrer n'est à toutes fins pratiques jamais utilisée à cet effet.

La chambre de Debye-Scherrer est un dispositif relativement simple, qui consiste en une chambre de forme cylindrique, un porte échantillon positionné en son centre et une source monochromatique.

Représentation de l'intérieur de la chambre

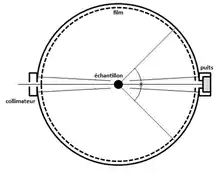
La source monochromatique produit des rayons incidents qui traversent un collimateur qui sert à limiter le faisceau incident à son entrée dans l’appareil. Les rayons, une fois collimatés, frappent l’échantillon de poudre et sont diffractés sous la forme de cônes. Les cônes formés par les rayons diffractés forment des anneaux elliptiques sur le cliché.

Une pellicule de film est placée sur les parois de la chambre et sert à photographier les anneaux de diffraction. Pour faciliter la lecture du cliché, la chambre est par convention, construite de façon que sa circonférence soit égale à 360 millimètres ou à 180 millimètres. De cette façon, la mesure en millimètre des distances entre les anneaux de diffraction et le centre de la pellicule peut facilement être convertie en une valeur d’angle de diffraction. Le faisceau primaire est donc recueilli dans un puits. La collecte du faisceau primaire influence la qualité du cliché puisque la précision des données dépend du contraste entre les anneaux de diffraction et le reste du film. La chambre n’étant pas isolée, il y aura diffusion des rayons X par les molécules d’air et en plus de la création d’un voile par rayonnement parasite. Il est donc important de recueillir le rayonnement primaire le plus près possible de l’échantillon[2].

L'utilisation d'une source de rayons X quasi-monochromatique présente généralement les radiations ${\displaystyle \lambda _{K\alpha 1}}$ et ${\displaystyle \lambda _{K\alpha 2}}$. Cela a pour effet de dédoubler certains anneaux de diffractions sur le cliché. Il est possible de distinguer clairement des anneaux pour des angles supérieurs à 15°. Le traitement des doublets va dépendre de si les doublets sont résolus, c'est-à-dire s’il est facile de les distinguer l’un de l’autre ou non. Si les doublets sont résolus, il est conseillé d’associer l’anneau extérieur à ${\displaystyle \lambda _{K\alpha 1}}$ et l’angle intérieur à ${\displaystyle \lambda _{K\alpha 2}}$ Si les doublets sont non résolus, il est préférable d’utiliser le centre de la raie et de lui associer une longueur d’onde correspondant à 1/3 * (2*${\displaystyle \lambda _{K\alpha 1}}$ + ${\displaystyle \lambda _{K\alpha 2}}$). De cette façon, le calcul tient compte de la différence d'intensité théorique plus grande de ${\displaystyle \lambda _{K\alpha 1}}$ que de ${\displaystyle \lambda _{K\alpha 2}}$[4].

La longueur d’arc S d’un cône de diffraction peut s’écrire comme ${\displaystyle S=x-x'}$, où x et x’ représentent les positions respectives des deux intersections du cône étudié avec le film plan.

Schéma d’un cliché par la méthode de Debye-Scherrer

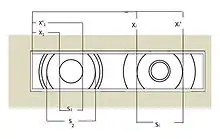
La position de la première perforation par laquelle le faisceau entre, à gauche, est alors située en ${\displaystyle X_{m1}={\frac {x_{1}+x'_{1}}{2}}}$.

En prenant la moyenne pour chaque cône de diffraction autour de cette perforation, il est alors possible de trouver la position relative du premier orifice par rapport à l’extrémité du film. Cette étape doit ensuite être répétée pour le deuxième trou de notre film dont la position entre deux franges d’un même cône est donnée par ${\displaystyle X_{m2}={\frac {x_{i}+x'_{i}}{2}}}$.

Afin de faciliter l’extrapolation des données, les chambres de Debye-Scherrer ont usuellement un diamètre qui permettra de convertir une distance métrique sur le plan en une valeur angulaire dans la chambre aisément. Ainsi, pour un cliché de caméra de diamètre de ${\displaystyle 57.26mm}$ (équivalent à ${\displaystyle 180/\pi )}$, on trouverait théoriquement ${\displaystyle X_{m2moyen}-X_{m1moyen}=180mm}$ (ou ${\displaystyle 90mm}$ pour une caméra de diamètre ${\displaystyle 28.63mm}$ (équivalent à ${\displaystyle 90/\pi ))}$.

Toutefois, il est possible que l’âge de la pellicule ou encore une contraction de celle-ci lors du développement, fasse en sorte que la valeur expérimentale diffère de la valeur théoriquement attendue. Dans un tel cas, il est nécessaire d’appliquer un facteur de correction ${\displaystyle p}$ que l’on obtient avec :

${\displaystyle p={\frac {90-(X_{m2moyen}-X_{m1moyen})}{X_{m2moyen}-X_{m1moyen}}}}$.

Dans le cas où l’on a à appliquer ce facteur, la longueur d’arc corrigée ${\displaystyle S'}$ est définie par ${\displaystyle S(1+p)}$. Sachant que la longueur d’arc ${\displaystyle S=4\theta R}$, on trouve la relation suivante ${\displaystyle \theta ={\frac {180S}{4\pi R}}}$ en degrés.

De là, pour trouver la valeur de l’angle de diffraction en fonction de la longueur d’arc S mesurée sur le cliché, il suffit d’utiliser la relation suivante : ${\displaystyle \theta ={\frac {S}{4}}}$ pour un diamètre de caméra de ${\displaystyle 57.26mm}$ ou ${\displaystyle {\frac {S}{2}}}$ pour un diamètre de ${\displaystyle 28.63mm}$.

Ensuite, la loi de Bragg permet de déterminer les distances interréticulaires ${\displaystyle d_{hkl}}$ correspondantes à chaque valeur de déviation ${\displaystyle \theta }$ avec :

${\displaystyle d_{hkl}={\frac {\lambda }{2\cdot \sin \theta }}}$

Finalement, si le système cristallin du matériau étudié est connu, deux méthodes permettent ensuite de déterminer le paramètres de maille de la poudre, soit l’étude avec l’analyseur cubique et l’indexation des plans.

Lorsque le système cristallin de la poudre étudiée est connu, et que celui-ci s’avère d’être cubique, la méthode graphique de l’analyseur cubique permet d’indexer rapidement les anneaux de diffraction tout en donnant une idée relativement précise du paramètre de maille de la poudre analysée. La technique consiste à tracer les droites du paramètres de maille ${\displaystyle a}$ en fonction de ${\displaystyle d_{hkl}}$ pour plusieurs indices de plans sur le même graphique. Après avoir tracé des lignes horizontales pour chaque distance interréticulaire ayant diffracté dans la chambre de Debye-Scherrer, il est possible de déterminer approximativement la valeur du paramètre de maille recherché en trouvant la valeur de ${\displaystyle a}$ pour laquelle chaque ligne verticale intercepte une droite de l’analyseur[5].

L’indexation des plans est une méthode pour identifier les plans qui correspondent aux angles de Bragg des différents anneaux de diffraction. À partir des valeurs de ${\displaystyle d_{hkl}}$ obtenues en analysant le film de diffraction et en connaissant le système cristallin de l’échantillon, il est possible de déterminer les indices (hkl) correspondants à ces valeurs avec la méthode d’indexation des plans.

La méthode peut être résumée à l’aide du tableau suivant, où les étapes vont chronologiquement de gauche à droite :

Angle de Bragg	Distance interréticulaire	Coefficient C	Entier N	Indices du plan	Paramètre de maille
${\displaystyle \theta ={\frac {S}{2}}}$ ou ${\displaystyle {\frac {S}{4}}}$	${\displaystyle d_{hkl}={\frac {\lambda }{2\cdot \sin \theta }}}$	${\displaystyle C={\frac {1}{d_{hkl}^{2}}}}$	${\displaystyle N=f\cdot {\frac {C}{min(C)}}}$	${\displaystyle h^{2}+k^{2}+l^{2}=N}$	${\displaystyle a={d_{hkl}}{\sqrt {h^{2}+k^{2}+l^{2}}}}$

Pour une maille cubique, le paramètre de maille ${\displaystyle a}$ suit la relation ${\displaystyle d_{hkl}={\frac {a}{\sqrt {h^{2}+k^{2}+l^{2}}}}}$. La relation étant généralement plus compliquée pour les autres familles cristallines, la méthode exprimée ici ne serait pas appropriée pour indexer des plans dans ces réseaux de Bravais.

Ainsi, pour une maille cubique, on peut remarquer que la somme ${\displaystyle h^{2}+k^{2}+l^{2}}$ est proportionnelle à ${\displaystyle {\frac {1}{d_{hkl}^{2}}}}$. Pour chaque distance interréticulaire ${\displaystyle d_{hkl}}$ trouvée, il faut alors évaluer la valeur d’un coefficient ${\displaystyle C={\frac {1}{d_{hkl}^{2}}}}$. De là, il faut ensuite normaliser les résultats obtenus selon la plus petite valeur, c’est-à-dire de diviser chaque valeur de ${\displaystyle C}$ par la plus petite. Il en résulte alors un ensemble de valeurs de normalisation supérieures ou égales à 1. En multipliant celles-ci par un facteur de multiplication ${\displaystyle f}$, il faut ensuite tenter d’obtenir des valeurs ${\displaystyle N}$ le plus près possible d’un nombre entier. On peut simplement évaluer ce facteur par essais erreurs, en sachant justement que celui-ci est généralement proche de 1, soit 1, 2, 3, 4, etc. Toutefois, si une valeur normalisée donne le nombre 7, il est important de multiplier d’un facteur 2 l'ensemble des valeurs, car il est mathématiquement impossible d’obtenir cette somme en additionnant trois carrés de nombre naturels.

À partir de là, il est possible d’indexer chaque valeur entière N obtenue à un plan de diffraction puisqu’elles sont la somme des carrés des indices de Miller associés à ce plan. Finalement, en étudiant ces valeurs entières, il est également possible de reconnaître le mode du réseau cristallin cubique du matériau grâce aux extinctions systématiques associées à chaque mode, c’est-à-dire en remarquant les valeurs de N manquantes. Enfin, le paramètre de maille ${\displaystyle a}$ de la poudre étudiée est obtenu par :

${\displaystyle a={d_{hkl}}{\sqrt {h^{2}+k^{2}+l^{2}}}}$