Méplat (mathématiques)

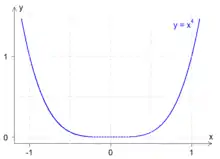
La courbe d'équation ${\displaystyle y=x^{4}}$ présente un méplat en ${\displaystyle x=0}$.

Dans un repère cartésien ${\displaystyle \{x,y\}}$, le graphe ${\displaystyle y=f(x)}$ d'une fonction ${\displaystyle f}$ présente un méplat à l'abscisse ${\displaystyle x_{0}}$ si :

${\displaystyle {\begin{cases}f''(x_{0})=f'''(x_{0})=0\\f^{(4)}(x_{0})\neq 0\end{cases}}}$

ou, plus généralement, s'il existe un entier pair ${\displaystyle k}$ supérieur à ${\displaystyle 2}$, tel que ${\displaystyle f}$ soit dérivable au moins ${\displaystyle k}$ fois en ${\displaystyle x_{0}}$ et que :

${\displaystyle {\begin{cases}f^{(n)}(x_{0})=0\quad {\text{pour}}\quad n=2,\dots ,k-1\\f^{(k)}(x_{0})\neq 0\end{cases}}}$

Le point ${\displaystyle (x_{0},f(x_{0}))}$ est un point méplat. La courbure en ${\displaystyle x=x_{0}}$ est nulle, et elle a le même signe de part et d'autre de ${\displaystyle x_{0}}$ (pour ${\displaystyle x=x_{0}-\varepsilon \,}$ et ${\displaystyle \,x=x_{0}+\varepsilon }$, où ${\displaystyle \varepsilon }$ désigne un infiniment petit), ce qui distingue les points méplats des points d'inflexion.

Un méplat (ou point planaire) d'une surface S est un point où les deux courbures principales sont nulles.