Mécanisme à développement rectiligne
Un mécanisme à développement rectiligne est un mécanisme qui produit une ligne droite parfaite ou approximative. Le premier mécanisme connu pour produire un mouvement en ligne droite était une approximation, décrite en 1784 par James Watt.
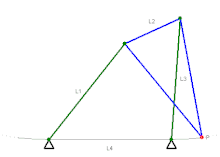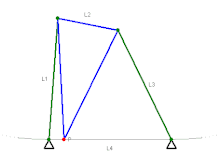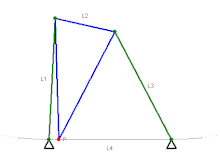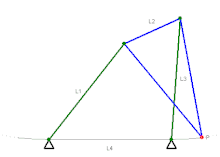
Les barres de même couleurs ont la même longueur.
Les pièces de même couleurs ont la même longueur.
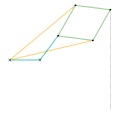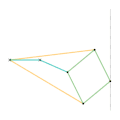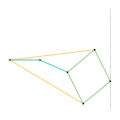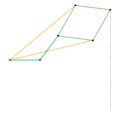
Les barres de même couleurs ont la même longueur.
Ils sont utilisés dans une variété d'applications, telles que les moteurs, les suspensions de véhicules, les robots marcheurs et les roues de rover.
Histoire
À la fin du XVIIe siècle, avant le développement de la raboteuse et de la fraiseuse plane, il était extrêmement difficile d’usiner des surfaces droites et planes. Pour cette raison, de bonnes liaisons glissières, sans jeu, ne sont pas faciles à réaliser. À cette époque, beaucoup de recherches furent consacrées au problème de l'obtention d'un mouvement rectiligne à partir du mouvement d’un réseau de barres lié par des liaisons pivots : on compte 150 articles publiés à ce sujet dans des revues de mathématiques ou de mécanique sur l'ensemble du XIXe siècle[1]. Probablement, le résultat le plus connu de ces recherches est le développement du mécanisme à développement rectiligne, par James Watt pour guider le piston des premiers moteurs à vapeur. Bien qu’il ne génère pas une ligne droite exacte, il en réalise une bonne approximation sur une très grande partie du déplacement. James Watt aurait retiré plus de fierté de ce mécanisme que de l'invention du moteur à vapeur[1].
Mécanismes à sortie quasi rectiligne
- Mécanisme de Watt (1784[1])
- Mécanisme Parallélogramme de Watt (1784)
- Mécanisme de Evans (1801)
- Mécanisme de Tchebychev (1850[1]) (transforme un mouvement de rotation uniforme en mouvement quasi linéaire à vitesse quasi constante)
- Mécanisme lambda de Tchebychev (1878)
- Mécanisme de Roberts
- Mécanisme de Hoecken (1926)
Mécanismes à sortie parfaitement rectiligne
Finalement, plusieurs mécanismes furent inventés pour obtenir une sortie parfaitement linéaire:
- Mécanisme de Sarrus (1853[1])
- Inverseur de Peaucellier-Lipkin (1864[1])
- Inverseur de Hart (1874[1])
- Inverseur de Perrolatz
- Inverseur Deux Cerf-volant de Kempe (1875)
- Inverseur de Bricard
- Inverseur Quadruplanaire (1875)
D'un point de vue théorique, on peut montrer qu'il n'est pas possible de concevoir un mécanisme bidimensionnel à sortie parfaitement rectiligne avec moins de cinq tiges[1]. En ce sens l'inverseur de Hart peut donc être considéré comme optimal.
Galerie
Mécanismes à sortie quasi rectiligne
Les pièces/barres de même couleurs ont la même longueur.
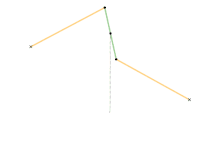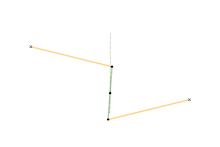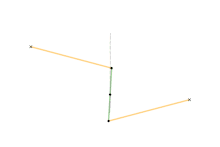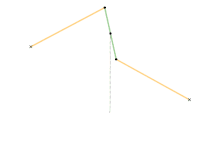 Mécanisme de Watt
Mécanisme de Watt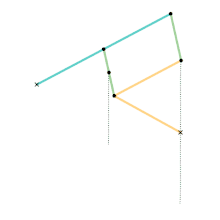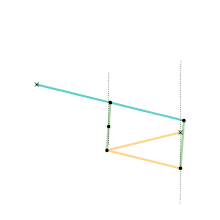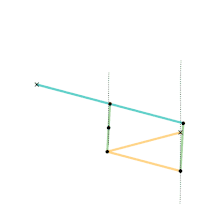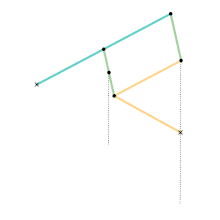 Mécanisme Parallélogramme de Watt
Mécanisme Parallélogramme de Watt Mécanisme de Evans
Mécanisme de Evans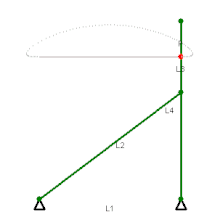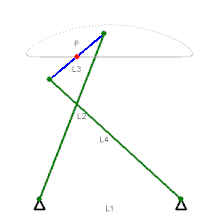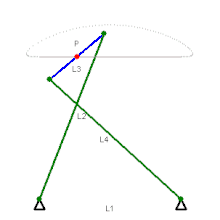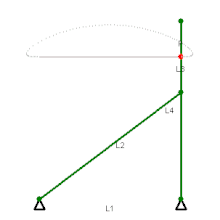 Mécanisme de Tchebychev
Mécanisme de Tchebychev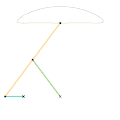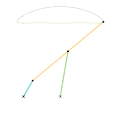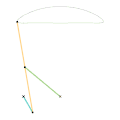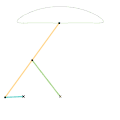 Mécanisme lambda de Tchebychev
Mécanisme lambda de Tchebychev Mécanisme table de Tchebychev
Mécanisme table de Tchebychev Mécanisme de Roberts
Mécanisme de Roberts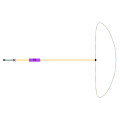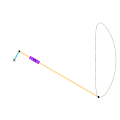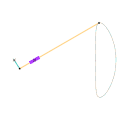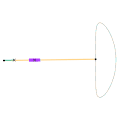 Mécanisme de Hoecken
Mécanisme de Hoecken
Mécanismes à sortie parfaitement rectiligne
Les pièces/barres de même couleurs ont la même longueur.
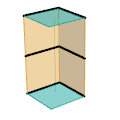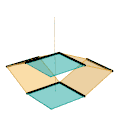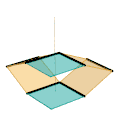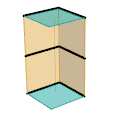
 Mécanisme de Sarrus (Variante de barres)
Mécanisme de Sarrus (Variante de barres) Mécanisme de Sarrus (Variante de plaque)
Mécanisme de Sarrus (Variante de plaque) Inverseur de Peaucellier-Lipkin
Inverseur de Peaucellier-Lipkin Inverseur de Harts 1
Inverseur de Harts 1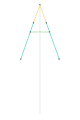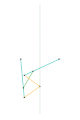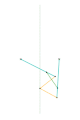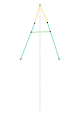 Inverseur de Harts 2
Inverseur de Harts 2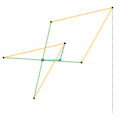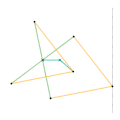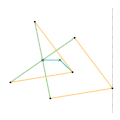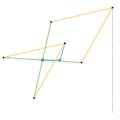 Inverseur de Perrolatz
Inverseur de Perrolatz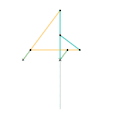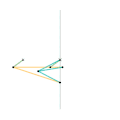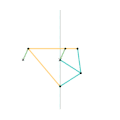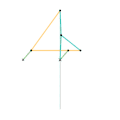 Inverseur de Kempe 1
Inverseur de Kempe 1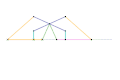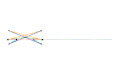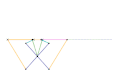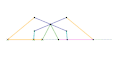 Inverseur de Kempe 2
Inverseur de Kempe 2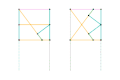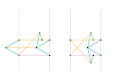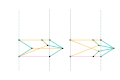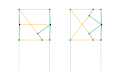 Inverseur de Kempe 3
Inverseur de Kempe 3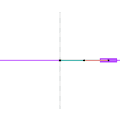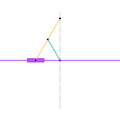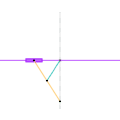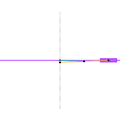 Mécanisme de Scott Russell (connexion curseur)
Mécanisme de Scott Russell (connexion curseur)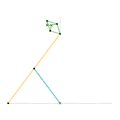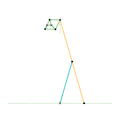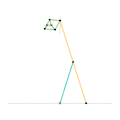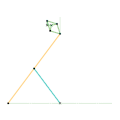 Mécanisme de Scott Russell (Connecté à Inverseur de Peaucellier-Lipkin)
Mécanisme de Scott Russell (Connecté à Inverseur de Peaucellier-Lipkin)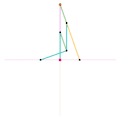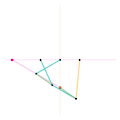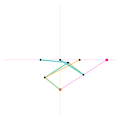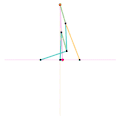 Inverseur de Bricard
Inverseur de Bricard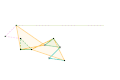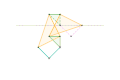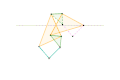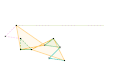 Inverseur Quadruplanaire de Sylvester-Kempe 1
Inverseur Quadruplanaire de Sylvester-Kempe 1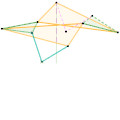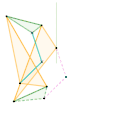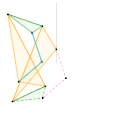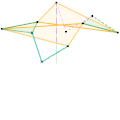 Inverseur Quadruplanaire de Sylvester-Kempe 2
Inverseur Quadruplanaire de Sylvester-Kempe 2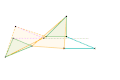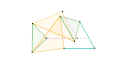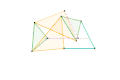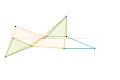 Inverseur Quadruplanaire de Sylvester-Kempe 3
Inverseur Quadruplanaire de Sylvester-Kempe 3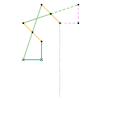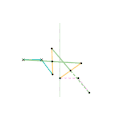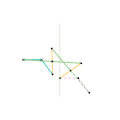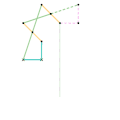 Inverseur de Kumara-Kampling
Inverseur de Kumara-Kampling
Voir aussi
- Mécanisme à quatre barres
- Grue à flèche
- Actionneur à chaîne rigide
Sources
- Franco Conti, Scuola Normale Superiore, « Courbes et mécanisme », dans Enrico Giusti, Franco Conti, Au-delà du compas : La géométrie des courbes, , 91 p. (ISBN 88-8263-015-3).
- Theory of Machines and Mechanisms, Joseph Edward Shigley
Liens externes
- Cornell university - Modèle de mécanisme à développement rectiligne
- Cornell university - "How to Draw a Straight Line" par A.B. Kempe
- Cornell university - "How to Draw a Straight Line" - tutoriel par Daina Taimina
- Simulations utilisantr le logiciel Molecular Workbench
- bham.ac.uk - Mécanisme à 6 barres de l'inverseur de Hart (animation)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Straight line mechanism » (voir la liste des auteurs).