Dispositif de Peaucellier-Lipkin
Le dispositif de Peaucellier-Lipkin est un système articulé permettant de transformer un mouvement rectiligne en mouvement circulaire, et vice-versa.
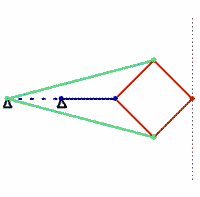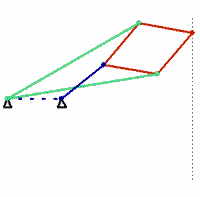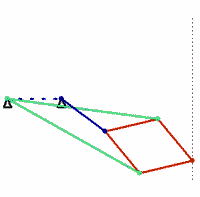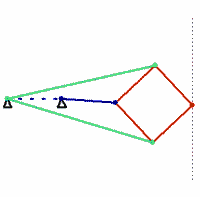
Inventé en 1864 et nommé d'après l'officier français Charles Peaucellier (1832-1919) et le Lituanien Lipman Lipkin, il s'agit du premier dispositif plan permettant une telle transformation. Il repose sur le principe géométrique de l'inversion d'un cercle.
Nom
Le système est désigné par des noms variables, « dispositif », « mécanisme », « inverseur » ou « parallélépipède ». Le nom de Charles Peaucellier est généralement présent, accolé ou non à celui de Lipman Lipkin.
Principe
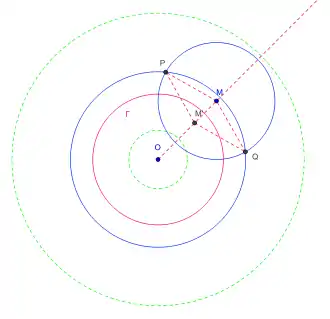
Le principe du dispositif est basé sur l'inversion d'un cercle.
Pour un point du plan affine euclidien et un rapport , avec , on peut construire l'inverse géométrique, pour l'inversion de centre et de rapport , de tout point dans la couronne centrée en , de rayon intérieur , et de rayon extérieur de la façon suivante :
- Un point dans la couronne étant donné, il existe deux points d'intersection et du cercle de centre et de rayon , et du cercle de centre et de rayon
- Puis on construit l'unique point tel que soit un losange.
- L'application qui à fait correspondre est bien l'inversion cherchée.
Le dispositif de Peaucellier-Lipkin est la transcription mécanique de cette inversion.
Historique
Les mécanismes permettant de transformer un mouvement circulaire en un mouvement rectiligne approximatif existent depuis plusieurs siècles, mais ils nécessitent cependant des guides afin de fonctionner. Le parallélogramme de Watt, inventé par James Watt en 1784 pour sa machine à vapeur, est le premier mécanisme planaire effectuant une telle transformation uniquement à l'aide de liaisons, mais elle reste approximative[1].
La question de savoir s'il existe un dispositif plan permettant cette transformation est soulevée par Charles Peaucellier en 1864 dans une correspondance aux Nouvelles annales de mathématiques, mais sans en expliciter la solution[2]. En 1868, il conçoit un appareil pour mesurer les distances qu'il décrit dans le Mémorial de l'Officier du Génie[3] - [4]. En 1871, Lipman Lipkin décrit de façon indépendante le même principe dans la Revue universelle des Mines et de la Métallurgie de Liège[5] - [4]. Peaucellier est un officier du génie français. Lipkin est un Juif lituanien étudiant à Saint-Pétersbourg, fils du rabbin Israël de Salant[6]. Les travaux de Peaucellier suscitent peu d'attention au moment de leur publication, au contraire de Lipkin qui est honoré par le gouvernement russe[1].
Le mécanisme de Peaucellier-Lipkin utilise sept tiges rigides. Il est en fait possible de résoudre le problème du mouvement rectiligne avec moins, le minimum étant de cinq tiges comme dans l'inverseur de Hart, inventé en 1874, soit moins de dix ans après les travaux de Peaucellier[1].
Applications
Le dispositif de Peaucellier-Lipkin a été utilisé dès 1877 dans le système de ventilation du Parlement de Londres[1].
Annexes
Liens internes
Liens externes
- Inverseur de Peaucellier, figure interactive sur ChronoMath
- (fr) Inversion de cercles
- (en) How to draw an exact straight line
- (en) How to Draw a Straight Line
- (en) Peaucellier Linkage (applet Java)
- (en) Peaucellier Linkage (applet Java)
- (en) Peaucellier Apparatus
- (en) Straight line mechanisms
Références
- Franco Conti, Scuola Normale Superiore, « Courbes et mécanisme », dans Enrico Giusti, Franco Conti, Au-delà du compas : La géométrie des courbes, , 91 p. (ISBN 88-8263-015-3).
- [PDF] Camille-Christophe Gerono, « Lettre de M. Peaucellier, capitaine du Génie (à Nice) », Nouvelles annales de mathématiques, 2e série, vol. ΙΙΙ, , p. 414-416 (lire en ligne)
- Charles Peaucellier et Wagner, « Mémoire sur un appareil diastimométrique nouveau dit appareil autoréducteur », Mémorial de l'officier du Génie, vol. 18, , p. 257-350
- [PDF] Émile Lemoine, « Note sur le losange articulé du commandant du génie Peaucellier, destiné à remplacer le parallélogramme de Watt », Journal de physique théorique et appliquée, vol. 2, no 1, , p. 130-134 (DOI 10.1051/jphystap:018730020013001, lire en ligne)
- Lipman Lipkin, « Dispositif articulé pour la transformation rigoureuse du mouvement circulaire en mouvement rectiligne », Revue universelle des Mines et de la Métallurgie de Liège, vol. XXX, , p. 149-150
- Daina Taimiņa, « How to draw a straight line »
Bibliographie
- (en) Ogilvy CS, Excursions in Geometry, New York, Dover, , 178 p. (ISBN 0-486-26530-7)
- Coxeter HSM, Greitzer SL, Geometry Revisited, Washington, MAA, , 193 p. (ISBN 978-0-88385-619-2, lire en ligne)
- Hartenberg, R.S. & J. Denavit (1964) Kinematic synthesis of linkages, p. 181–5, New York: McGraw-Hill
- Johnson RA, Advanced Euclidean Geometry : An elementary treatise on the geometry of the triangle and the circle, New York, Dover Publications, , 319 p. (ISBN 978-0-486-46237-0, lire en ligne)
- (en) Wells D, The Penguin Dictionary of Curious and Interesting Geometry, New York, Penguin Books, , 285 p. (ISBN 0-14-011813-6)












