La loxodromie constitue un arc sur la sphère que l'on suppose défini par une fonction de classe  :
:  , et orienté dans le sens des longitudes croissantes. Soit la fonction
, et orienté dans le sens des longitudes croissantes. Soit la fonction  qui, à la longitude
qui, à la longitude  , associe le point courant de la loxodromie de longitude
, associe le point courant de la loxodromie de longitude  et de latitude
et de latitude  .
.
Un vecteur tangent à la loxodromie est alors  . Ce vecteur, qui dirige la tangente à l'arc, forme donc, par hypothèse, un angle
. Ce vecteur, qui dirige la tangente à l'arc, forme donc, par hypothèse, un angle  avec tout vecteur (non nul) dirigeant le méridien au point considéré. Un vecteur dirigeant le méridien en
avec tout vecteur (non nul) dirigeant le méridien au point considéré. Un vecteur dirigeant le méridien en  est
est  , tandis qu'un vecteur dirigeant le parallèle est
, tandis qu'un vecteur dirigeant le parallèle est  .
.
Dans la suite, pour alléger l'écriture, on ne précisera plus le point  , auquel sont prises les fonctions et leurs dérivées partielles, et on notera
, auquel sont prises les fonctions et leurs dérivées partielles, et on notera  au lieu de
au lieu de  , et
, et  la dérivée de
la dérivée de  par rapport à
par rapport à  .
.
En effectuant le produit scalaire d'un vecteur directeur de la tangente à la loxodromie et d'un vecteur directeur du méridien, on obtient le produit des normes de ces vecteurs par le cosinus de l'angle qu'ils forment. Cet angle est précisément le cap vrai  lorsque
lorsque  :
:
 , en notant
, en notant  le produit scalaire
le produit scalaire  par
par  .
.
Comme les parallèles et les méridiens sont perpendiculaires, les vecteurs  et
et  sont orthogonaux, et l'expression précédente se simplifie en :
sont orthogonaux, et l'expression précédente se simplifie en :

puis en :

En élevant au carré et en utilisant le théorème de Pythagore, on obtient :

D'où, avec 
 .
.
On calcule les deux normes intervenant dans cette équation :
On sait, d'après le paramétrage sphérique rapporté aux coordonnées cartésiennes dans la base  ,
,  étant dirigé selon l'axe terrestre, que
étant dirigé selon l'axe terrestre, que  , où
, où  est le vecteur unitaire radial du plan équatorial défini par :
est le vecteur unitaire radial du plan équatorial défini par :  .
On définit
.
On définit  comme le vecteur dérivé par rapport à
comme le vecteur dérivé par rapport à  de
de  :
:  .
Alors
.
Alors  et
et  . Ainsi,
. Ainsi,  et
et  .
.
L'équation  se réduit à :
se réduit à :

Si on suppose qu'on part de l'équateur ( ) à la longitude
) à la longitude  et qu'on se dirige vers le Nord-Est, alors
et qu'on se dirige vers le Nord-Est, alors ![{\displaystyle R_{v}\in \,]0,\pi /2[}](https://img.franco.wiki/i/4e08517600af9fe05e882a28ac1778fa8eaee38e.svg) , et
, et  est une fonction croissante de
est une fonction croissante de  donc
donc  (dans les autres cas, on déduit l'arc par une symétrie centrale et/ou une rotation convenable(s), donc on ne perd pas de généralité), par suite :
(dans les autres cas, on déduit l'arc par une symétrie centrale et/ou une rotation convenable(s), donc on ne perd pas de généralité), par suite :

- et
 , équation différentielle non linéaire à variables séparables en
, équation différentielle non linéaire à variables séparables en 
En intégrant entre 0 et  :
:
 ,
,- soit (cf. Primitives de fonctions trigonométriques)

La longueur L parcourue vaut alors, par définition :

- où
 et
et  et, pour les mêmes raisons de signe,
et, pour les mêmes raisons de signe,  .
.

En changeant de variable, avec  avec
avec
 la latitude variant de 0 à
la latitude variant de 0 à  quand
quand  varie de 0 à
varie de 0 à  :
:
- On a


Il est facile de vérifier le résultat en prenant  nul. On voit que l'arc parcouru est le méridien et sa longueur est égale au quart de la circonférence.
nul. On voit que l'arc parcouru est le méridien et sa longueur est égale au quart de la circonférence.
Le même calcul mené entre deux points A et B situés sur la loxodromie donnera comme longueur :

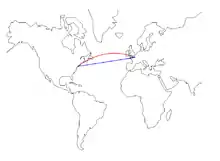


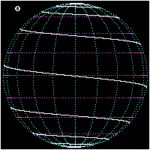 Loxodromie vue de l'équateur
Loxodromie vue de l'équateur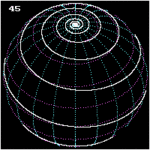
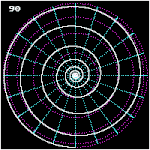 Loxodromie vue du pôle nord
Loxodromie vue du pôle nord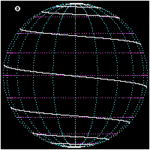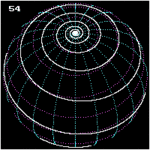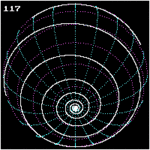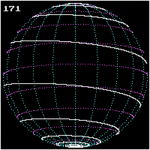







![{\displaystyle ^{[nq]}}](https://img.franco.wiki/i/7f8d4abc0a2380b84db95e4e32891c8dd692877d.svg)
![{\displaystyle ^{[rad]}}](https://img.franco.wiki/i/3b4d802dde1c3ec5addc886c895cb3c8e3438028.svg)
![{\displaystyle ^{[,]}}](https://img.franco.wiki/i/a6cf5bdbac666e0b7bc71fd3d91ae54e431a636a.svg)
![{\displaystyle M^{[nq]}={\frac {\varphi _{B}\,^{[,]}-\varphi _{A}\,^{[,]}}{\cos R_{v}}}\,}](https://img.franco.wiki/i/f410fa52da50ffe82803c95698cc09c380750989.svg)



![{\displaystyle \lambda =\ln \tan \left({\frac {\pi }{4}}+{\frac {\varphi ^{[rad]}}{2}}\right)\,}](https://img.franco.wiki/i/e42336073126d41b5321dc9ade2b38d5f60e3f59.svg)

![{\displaystyle M^{[nq]}={\frac {\left|G_{B}\,^{[,]}-G_{A}\,^{[,]}\right|\cos \varphi _{m}}{\sin Rf_{q}}}}](https://img.franco.wiki/i/9c816e6929ed8032b8df66057b87f8633562d71b.svg)
![]0,\pi [](https://img.franco.wiki/i/7f7fa6582460166e2c164b5be01af3bf4a430820.svg)
![{\displaystyle R_{v}\in \,]0,\pi /2[}](https://img.franco.wiki/i/4e08517600af9fe05e882a28ac1778fa8eaee38e.svg)























































