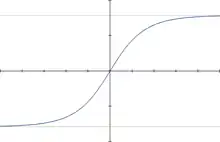
Fonction de Gudermann

Graphe de la fonction de Gudermann avec ses deux asymptotes horizontales : ${\displaystyle \theta =\pm {\frac {\pi }{2}}}$.

La fonction de Gudermann est définie sur l'ensemble des réels par :

${\displaystyle {\begin{aligned}{\operatorname {gd} }(t)&=\int _{0}^{t}{\frac {\mathrm {d} u}{\cosh u}}\\&=\arcsin \left(\tanh t\right)=\operatorname {signe} (t)\cdot \arccos \left(\operatorname {sech} t\right)\ \\&=\arctan \left(\sinh t\right)=\operatorname {signe} (t)\cdot \operatorname {arcsec} \left(\cosh t\right)\\&=\operatorname {arccot} \left(\operatorname {csch} t\right)=\operatorname {arccsc} \left(\coth t\right)\\&=2\arctan \left(\tanh {\frac {t}{2}}\right)=2\arctan e^{t}-{\frac {\pi }{2}}.\end{aligned}}}$

Le réel ${\displaystyle \theta =\operatorname {gd} (t)}$, appelé parfois gudermannien de ${\displaystyle t}$, est relié à ce dernier par les relations :

${\displaystyle {\begin{aligned}{\sin \theta }&=\tanh t~;\quad \cos \theta ={\frac {1}{\cosh t}}=\operatorname {sech} t~;\\\tan \theta &=\sinh t~;\quad \tan {\frac {\theta }{2}}=\tanh {\frac {t}{2}}.\end{aligned}}}$

La dérivée de la fonction de Gudermann ${\displaystyle t\mapsto \theta }$ est donnée par ${\displaystyle {\frac {\mathrm {d} \theta }{\mathrm {d} t}}={\frac {1}{\cosh t}}=\cos \theta }$.

La fonction de Gudermann est donc la solution s'annulant en 0 de l'équation différentielle ${\displaystyle y'=\cos y}$.

La réciproque de la fonction de Gudermann est définie sur ${\displaystyle ]-\pi /2,\pi /2[}$ par :

${\displaystyle {\begin{aligned}\operatorname {arcgd} (\theta )&={\rm {gd}}^{-1}(\theta )=\int _{0}^{\theta }{\frac {\mathrm {d} u}{\cos u}},\\&=\operatorname {argtanh} \sin \theta =\operatorname {signe} (\theta )\cdot \operatorname {argcosh} {\frac {1}{\cos \theta }},\\&={}\ln \left(\tan \theta +{\frac {1}{\cos \theta }}\right)=\ln \left(\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)\right),\\&={}{\frac {1}{2}}\ln {\frac {1+\sin \theta }{1-\sin \theta }}.\end{aligned}}}$

La dérivée de cette fonction réciproque ${\displaystyle \theta \mapsto t}$ est donnée par ${\displaystyle {\frac {\mathrm {d} t}{\mathrm {d} \theta }}={\frac {1}{\cos \theta }}=\cosh t}$.

La réciproque de la fonction de Gudermann est donc la solution s'annulant en 0 de l'équation différentielle ${\displaystyle y'=\cosh y}$.

• Les coordonnées de Mercator d'un point de la sphère sont définies par ${\displaystyle x=longitude}$ et ${\displaystyle y=\operatorname {gd} ^{-1}(latitude)}$.

Elles sont ainsi définies de sorte que les loxodromies de la sphère soient représentées par des droites dans le plan ${\displaystyle x,y}$.

• Le changement de variable ${\displaystyle \theta =\operatorname {gd} (t)}$ permet de transformer des intégrales de fonctions circulaires en intégrales de fonctions hyperboliques ; par exemple, ${\displaystyle \int _{0}^{\pi /2}{\cos ^{n}\theta .\mathrm {d} \theta }=\int _{0}^{+\infty }{\frac {\mathrm {d} t}{\cosh ^{n+1}t}}}$.
• Ceci explique pourquoi on peut choisir des fonctions circulaires ou hyperboliques lors de changement de variables dans le calcul d'intégrales :
  • quand on rencontre du ${\displaystyle {\sqrt {1-x^{2}}}}$, on utilise ${\displaystyle x=\cos \theta }$ ou ${\displaystyle x={\frac {1}{\cosh t}}}$, et on utilise aussi ${\displaystyle x=\sin \theta }$ ou ${\displaystyle x=\tanh t}$ ;
  • quand on rencontre du ${\displaystyle {\sqrt {1+x^{2}}}}$, on utilise ${\displaystyle x=\tan \theta }$ ou ${\displaystyle x=\sinh t}$.
• Paramétrisation d'un cercle ou d'une droite hyperbolique.

  Si l'on pose ${\displaystyle {\begin{cases}{\begin{aligned}x&=\cos \theta ={\frac {1}{\cosh t}}\\y&=\sin \theta =\tanh t\end{aligned}}\end{cases}}}$, on a évidemment une paramétrisation du demi-cercle de rayon 1 dans le demi-plan ${\displaystyle x>0}$ ; ${\displaystyle \theta }$ est la distance curviligne dans le demi-plan euclidien entre le point ${\displaystyle (x,y)}$ et le point ${\displaystyle (1,0)}$, et ${\displaystyle t}$ est aussi une distance, mais mesurée entre ces deux points dans le demi-plan considéré comme demi-plan de Poincaré pour la géométrie hyperbolique.

• Projection de Mercator
• Fonctions elliptiques de Jacobi

• (en) CRC Handbook of Mathematical Sciences 5th ed. pp 323–5.
• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gudermannian function » (voir la liste des auteurs).