Loi de Dollo
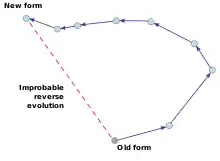
La loi de Dollo stipule qu'une spécialisation des espèces s'accompagne d'une diminution des mutations qui pourraient les faire évoluer, rendant improbable le retour des caractéristiques ou organes perdus par une espèce au cours de l'évolution.
Cette conjecture a été émise par le paléontologue Louis Dollo en 1893. Elle a été mise en avant par Stephen Jay Gould en 1970. Des exceptions à cette loi ont été découvertes au travers d'études de classification phylogénétiques et de tests de congruence informatisés.
Cette déclaration est souvent interprétée à tort comme affirmant que l'évolution n'est pas réversible[1], ou que les structures et organes perdus ne peuvent réapparaître sous la même forme par un quelconque processus de dévolution[2] - [3]. Selon Richard Dawkins, « la loi n'est en réalité qu'une déclaration sur l'improbabilité statistique de suivre deux fois exactement la même trajectoire évolutive (ou, en fait, toute trajectoire particulière), dans un sens ou dans l'autre »[4].
La loi de Dollo est composée de deux concepts :
- Un caractère complexe ayant été perdu au cours de l’évolution dans la lignée d'une espèce ne peut être récupéré par la suite.
- Les informations génétiques à la base du caractère perdu accumulent des mutations rendant le retour du caractère improbable[5].
Attention à ne pas confondre la loi de Dollo et un caractère réversible, par exemple une fleur de couleur blanche passe de la couleur blanche au rouge et redevient par la suite blanche. Un caractère réversible se produit à court terme sur le même organisme tandis que la loi de Dollo s’applique sur plusieurs générations et espèces au cours de l’évolution.
Attention à ne pas confondre ces deux situations :
- Une exception à la loi de Dollo où une structure a ré-évoluée de façon identique à la structure ancestrale qui avait été perdue au cours de l’évolution et donc partage les mêmes gènes et le même développement.
- Une convergence évolutive où la structure est similaire à une autre structure, mais elle s’est formée par des voies de développements distinctes et indépendantes l’une de l’autre.
Phylogénie et la loi de Dollo
La phylogénétique est utilisée pour observer la direction des changements au cours de l’évolution des caractères. Un arbre phylogénétique peut montrer un patron en accord ou en désaccord avec la loi de Dollo. Pour qu’un arbre phylogénétique corresponde à la loi de Dollo, il faut qu’un trait perdu ne soit jamais gagné par la suite. Un exemple possible est que sur un arbre le caractère est perdu 3 fois au cours de l’évolution et n'est jamais récupéré à la suite d’une perte. Un autre exemple d'arbre phylogénétique peut montrer un patron en désaccord avec la loi de Dollo. En effet, sur cet arbre le caractère est perdu et puis regagné par la suite donnant pour ce caractère 1 perte et 1 gain[5].
Méthodes phylogénétiques
La loi de Dollo assume par parcimonie qu’un gain de caractère n’arrive jamais si ce caractère a été perdu auparavant. Ainsi, des méthodes ont été élaborées pour tester l’irréversibilité de la loi de Dollo en estimant les probabilités de gains ou de pertes. La méthode du maximum de vraisemblance estime la probabilité de chaque caractère à chaque nœud afin de voir si l’état d’un caractère est significatif ou non. Ce test est un avantage par rapport à la parcimonie et a été utilisé à plusieurs reprises pour montrer des exceptions à la loi de Dollo. La méthode de Swofford-Olsen-Waddell-Hillis (SOWH) est utilisée pour voir si le meilleur arbre phylogénétique est significativement différent d’un autre arbre utilisant une autre démarche évolutive. Par exemple, ce test a été utilisé pour vérifier si l’arbre des lézards apodes du genre Bachia montrant le gain du nombre d’orteils est significativement différent de l’arbre montrant une perte du nombre d’orteils[5].
Génétique et la loi de Dollo
Les caractères complexes perdus sont dits impossible à être récupérés à cause de leurs gènes qui accumulent des mutations. Ainsi, la probabilité qu’une autre mutation inverse le caractère à son état initial est quasi-improbable.
Des études ont prédit et estimé le temps nécessaire pour que la structure perdue d’un gène retourne. Deux approches différentes ont été décrites. La première estime que pour un gène codant un caractère non utilisé, sa fonction peut être conservée jusqu’à 6 millions d’années, mais qu’après 10 millions d’années les mutations accumulées provoquent la perte de cette fonction du gène. L’autre approche estime que la demi-vie d’un gène codant un caractère non utilisé est de 4 millions d’années et qu’ainsi la fonction de ce gène sera perdue entre 16 et 24 millions d’années. Cependant, ces estimations de la durée de conservation d’une fonction non utilisée d’un gène concernent seulement les gènes ayant un seul effet ou codant une seule structure et donc ne concernent qu’un certain pourcentage de gène, par exemple l’hémoglobine.
En effet, plusieurs gènes ont plusieurs fonctions différentes ou contribuent à plusieurs caractères, c’est ce qu’on appelle la pléiotropie. Par exemple, les gènes au cours du début du développement sont exprimés à plusieurs sites. Le fait qu’un seul gène contribue à plusieurs caractères va permettre à conserver la fonction du gène malgré la perte d’un caractère, car les autres caractères sont toujours présents.
Un exemple connu est celui des dents chez les poulets. Dans la lignée des oiseaux modernes, les dents ont été perdus il y a plus de 60 millions d’années. Ainsi, dans les embryons des poulets, le développement des dents est perdu. Cependant, en examinant l’expression des gènes du développement des dents, on observe que la quasi-totalité est conservée et peut donc être réactivée. Cette conservation est due au fait que la fonction de ces gènes n’est pas unique au développement des dents, mais elle est aussi présente dans l’expression de d’autres structures tels que les plumes et les écailles[5].
Exemple expérimental d'une exception à la loi de Dollo
Les Gastéropodes ont perdu à plusieurs reprises dans l’évolution la caractéristique de l’enroulement de la coquille. À partir du moment où cette caractéristique est perdue, sa ré-évolution est dite improbable par la loi de Dollo. Pourtant, l’enroulement de la coquille procure divers avantages et est l’une des caractéristiques déterminant la diversité chez les gastropodes. Du coup, est-ce que la dizaine d’espèces ayant leur coquille enroulée chez les Calyptréidés, une famille des gastéropodes composée de près de 200 espèces, est un exemple d’une ré-évolution de ce caractère ou est-ce seulement que ce caractère ancestral n’est pas encore perdu pour ces espèces? Quelques exemples confirment que la ré-évolution d’un caractère est possible, notamment auprès des molaires des lynx et au niveau des ailes des insectes phasmosptères. Ces exemples sont des cas d’hétérotopies où les gènes du caractère interviennent aussi dans d’autres structures, mais ce n’est pas le cas de la coquille. Il a été proposé autrefois qu’une espèce de Gastéropodes, Petaloconchus sculpturatus, semblait avoir ré-évolué l’enroulement de la coquille comme son ancêtre, par contre ce n’était pas le cas. Ainsi, Collin fait une étude pour prouver que la ré-évolution de ce caractère est possible[6].
L’étude débute par la quantification du caractère de l’enroulement de la coquille de 184 coquilles de 46 espèces de calyptréidés. Trois variables permettent d’estimer la quantité : l’étanchéité de l’enroulement spiral, la longueur et le nombre de spirales dans la coquille. Ensuite, ils utilisent le séquençage de l’ADN pour former un arbre phylogénique des calyptréidés par parcimonie et analyse Bayésienne. Les résultats obtenus montrent que les espèces Trochita, Sigapatella et Zegalerus ont le caractère de l’enroulement de la coquille contrairement aux autres espèces. À l’aide de la phylogénie, il est possible de conclure que l’enroulement spiral est présent chez deux clades différents soit chez Trochita et chez Zegalerus et Sigapatella. Donc, un gain de ce caractère est nécessaire pour être en accord avec la phylogénie. En conclusion, la présence du caractère non présent chez les ancêtres directs de l’enroulement de la coquille chez certaines espèces de calyptréidés semble être un exemple de la ré-évolution d’un caractère et d’une exception à la loi de Dollo. La ré-évolution de ce caractère suggère que les gènes le contrôlant sont maintenus dans les ancêtres n’ayant pas le caractère. Ainsi, Collin propose que, contrairement aux autres exemples d’hétérotopies, la ré-évolution de ce caractère complexe est dû à un changement de la durée du développement. Ce serait donc le premier exemple d’hétérochronie[6].
Voir aussi
Bibliographie
- Louis Dollo, Les lois de l'évolution, vol. VII, coll. « Bull. Soc. Belge Geol. Pal. Hydr », (lire en ligne), p. 164-166
- G.J. de Fejérváry, « Quelques observations sur la loi de Dollo et l'épistréphogénèse en considération spéciale de la loi biogénétique de Haeckel », Bulletin de la Société Vaudoise des Sciences Naturelles, vol. 53, no 199, , p. 343-372 (BNF 34479314, lire en ligne).
- Louis Dollo, « Les Céphalopodes déroulés et l’irréversibilité de l’évolution », Bijdragen tot de Dierkunde, vol. 22, no 1, , p. 215-226 (ISSN 0067-8546, lire en ligne).
- Stephen Jay Gould, Dollo on Dollo's Law: Irreversibility and the Status of Evolutionary Laws, coll. « Journal of the History of Biology / 3, No.2:189-212 »,
- Collin, Rachel et Cipriani, R., « Dollo's law and the re-evolution of shell coiling », Proceedings of the Royal Society, vol. B 270, no 1533, , p. 2551–2555 (PMID 14728776, DOI 10.1098/rspb.2003.2517)
- Collin, Rachel et Maria Pia Miglietta, « Reversing opinions on Dollo's Law », Trends in Ecology & Evolution, vol. 23, no 11, 602–609 (PMID 18814933, DOI 10.1016/j.tree.2008.06.013)
- Michael Whiting, Sven Bradler et Taylor Maxwell, « Loss and recovery of wings in stick insects », Nature, vol. 421, , p. 264-267
- John J. Wiens, « Re-evolution of lost mandibular teeth in frogs after more than 200 million years and re-evaluationg Dollo'slaw », Evolution, vol. 65, no 5, , p. 1283-1296
- Vincent Lynch et Guenter Wagne, « Did egg-laying boas break Dollo's law phylogenetic evidence for reversal to oviparity in sand boas (Eryx boidae) », Evolution,
- Ryan Kerney David Blackburn Hendrick Mueller James Hanken, « Do larval traits re-evolve ? Evidence from the embryogneeis of a direct developing salamander Plethodon cinereus », Evolution, vol. 66, no 1, , p. 252-262
- Rui Diogo et Bernard Wood, « Violation of Dollo's law : evidence of muscle reversions in primate phylogeny and their implications for the understanding of the ontogeny evolution and atomical vairations of modern humans », Evolution, vol. 66, no 10, , p. 3267-3276
- « Ré-évolution et Loi de Dollo », L'Ingénieur, revue de l'association des Centraliens de Lille, no 281, , p. 3-4 (ISSN 0399-8304)
- Florian Maderspracher, « Evolution: They Never Come Back, or Do They? », Current biology, vol. 25, no 2, , R62–R64 (ISSN 0960-9822, DOI 10.1016/j.cub.2014.12.020, lire en ligne)
- Feifei Xu,Jon Jerlström-Hultqvist,Martin Kolisko,Alastair G. B. Simpson,Andrew J. Roger,Staffan G. Svärd and Jan O. Andersson, « On the reversibility of parasitism: adaptation to a free-living lifestyle via gene acquisitions in the diplomonad Trepomonas sp. PC1 », BMC Biology, vol. 14, no 62, (ISSN 1741-7007, DOI 10.1186/s12915-016-0284-z, lire en ligne)
- N. I. Mundy, N. C. Morningstar, A. L. Baden, E. Fernandez-Duque, V. M. Dávalos and B. J. Bradley, « Can colour vision re-evolve? Variation in the X-linked opsin locus of cathemeral Azara’s owl monkeys (Aotus azarae azarae) », Frontiers in Zoology, vol. 13, no 9, (DOI 10.1186/s12983-016-0139-z, lire en ligne).
- Odete Gonçalves, L. Filipe C. Castro, Adam J. Smolka, António Fontainhas, Jonathan M. Wilson, « The Gastric Phenotype in the Cypriniform Loaches: A Case of Reinvention? », PLoS ONE, vol. 11, no 10, (DOI 10.1371/journal.pone.0163696, lire en ligne).
- Yohe, L. R., Abubakar, R., Giordano, C., Dumont, E., Sears, K. E., Rossiter, S. J. and Dávalos, L. M., « Trpc2 pseudogenization dynamics in bats reveal ancestral vomeronasal signaling, then pervasive loss », Evolution, vol. 71, no 4, , p. 923–935 (DOI 10.1111/evo.13187).
- Gamble, T., Greenbaum, E., Jackman, T. R., Russell, A. P. and Bauer, A. M., « Repeated evolution of digital adhesion in geckos: a reply to Harrington and Reeder », Journal of Evolutionary Biology, vol. 30, no 7, , p. 1429–1436 (DOI 10.1111/jeb.13097).
Articles connexes
Notes et références
- Khalid O. Alfarouk, Mohammed E.A. Shayoub, Abdel Khalig Muddathir, Gamal O. Elhassan et Adil H.H. Bashir, « Evolution of Tumor Metabolism might Reflect Carcinogenesis as a Reverse Evolution process (Dismantling of Multicellularity) », Cancers, vol. 3, no 3, , p. 3002–3017 (PMID 24310356, PMCID 3759183, DOI 10.3390/cancers3033002
 )
) - Emma E. Goldberg et Boris Igić, « On phylogenetic tests of irreversible evolution », Evolution, vol. 62, no 11, , p. 2727–2741 (PMID 18764918, DOI 10.1111/j.1558-5646.2008.00505.x, S2CID 30703407)
- Rachel Collin et Maria Pia Miglietta, « Reversing opinions on Dollo's Law », Trends in Ecology & Evolution, vol. 23, no 11, , p. 602–609 (PMID 18814933, DOI 10.1016/j.tree.2008.06.013)
- Richard Dawkins, The Blind Watchmaker, W. W. Norton, (1re éd. 1986) (ISBN 978-0-393-31570-7, lire en ligne
 )
) - (en) Rachel Collin et Maria Pia Miglietta, « Reversing opinions on Dollo’s Law », Trends in Ecology & Evolution, vol. 23, no 11, , p. 602–609 (DOI 10.1016/j.tree.2008.06.013, lire en ligne, consulté le )
- (en) R. Collin et R. Cipriani, « Dollo's law and the re–evolution of shell coiling », Proceedings of the Royal Society of London. Series B: Biological Sciences, vol. 270, no 1533, , p. 2551–2555 (ISSN 0962-8452 et 1471-2954, PMID 14728776, PMCID PMC1691546, DOI 10.1098/rspb.2003.2517, lire en ligne, consulté le )