Lituus (courbe)
En géométrie, un lituus est une courbe plane d'équation polaire : Le nom de «lituus» lui est donné par Roger Cotes dans son Harmonia mensurarum[1] publié en 1722 en référence à la crosse étrusque de même nom. Cette courbe avait déjà été étudiée par Pierre Varignon en 1704 dans le cadre de son étude générale des spirales d'équation polaire pour m entier positif ou négatif[2].
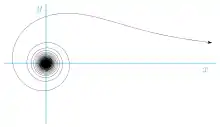
Propriétés géométriques
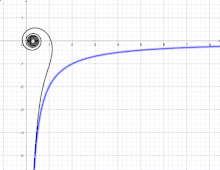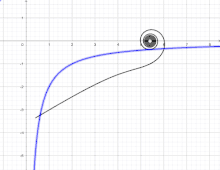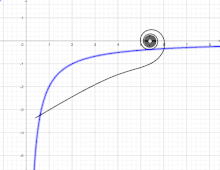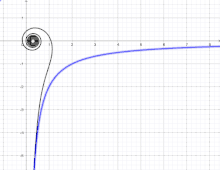
Le lituus est une courbe transcendante qui possède pour asymptotes son axe polaire et son pôle[3]. Il possède deux branches (pour ρ positif et pour ρ négatif) symétriques par rapport à O.
Pour tout point M situé sur la courbe, on appelle m le point d'intersection du cercle de centre O passant par M avec l'axe polaire. L'aire du secteur angulaire mOM est constant égale à a2/2[4].
Pour tout point M de la courbe, on appelle T le point d'intersection de la tangente avec la droite passant par O et perpendiculaire à (OM) alors la longueur OT est égale à 2a²/OM. Le lituus est donc une courbe dans laquelle la sous-tangente est inversement proportionnelle au rayon. L'aire du triangle OTM est constante égale au double de l'aire du secteur angulaire mOM[4].
L'aire balayée par le rayon OM de Md à Mf est proportionnelle au logarithme du rapport des rayons[5] - [4]:
Le rayon de courbure, pour une courbe paramétrée θ, a pour valeur[3]: et pour une courbe paramétrée par ρ, s'exprime par[4]: La courbe possède donc un point d'inflexion pour un rayon égal à a√2 et un angle de 1/2 rad.
Son abscisse curviligne est donnée par[3]: et la rectification de la courbe fait intervenir des intégrales elliptiques de deuxième espèce[4].
Relation avec d'autres courbes
Le lituus est l'image par une inversion, de pôle O et de cercle de rayon a, de la spirale de Fermat[3] d'équation polaire ρ2 = a2θ.
C'est également la radiale de la clothoïde[6].
Si on fait rouler le lituus sur l'hyperbole d'équation xy = –2a2, son centre se déplace sur l'axe des abscisses[7]. Cette propriété avait déjà été remarquée par Pierre Varignon en 1704[2].
Notes et références
- Cotes 1722.
- Varignon 1704.
- Mathcurve.
- Teixeira 1909.
- Cotes 1722, p. 86.
- Teixeira 1909, p. 110.
- Abolghassem Ahmad-Vaziri, « Sur quelsques courbes liées au mouvement d'une courbe plane dans son plan », dans Thèses de l'entre-deux-guerres, (lire en ligne), p.12.
Bibliographie
- (la) Roger Cotes, Harmonia mensurarum, Robert Smith, (lire en ligne), Pars Tertia Problème IV scholium p. 85
- Pierre Varignon, « Nouvelle formation des spirales - exemple II », Mémoire de l'académie des sciences de l'Institut de France, , p. 94 - 103 (lire en ligne).
- Francisco G. Teixeira, Obras sobre Mathematica : Traité des courbes spéciales remarquables planes et gauches, vol. V, Coimbra, Imprensa da Universidade, (lire en ligne), p. 74-76.
- Robert Ferreol, « Lituus », sur Encyclopédie des formes mathématiques remarquables, (consulté le )





