Liste d'adjacence
En algorithmique, une liste d'adjacence est une structure de données utilisée pour représenter un graphe.
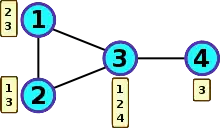
Cette représentation est particulièrement adaptée aux graphes creux (c'est-à-dire peu denses), contrairement à la matrice d'adjacence adaptée aux graphes denses.
Définition et propriétés
La liste d'adjacence d'un graphe non orienté, est la liste des voisins de chaque sommet[1]. Celle d'un graphe orienté est typiquement, pour chaque sommet, la liste de nœuds à la tête de chaque arête ayant le sommet comme queue.
C'est une représentation relativement compacte lorsqu'il y a peu d'arêtes (graphe creux), puisque la liste globale contient 2m éléments, où m est le nombre d'arêtes.
Implémentations
Une représentation par liste d'adjacence d'un graphe associe, à chaque sommet du graphe, la collection de ses voisins, comme sommets ou comme arêtes. Il existe de nombreuses variations de ce principe de base, qui diffèrent par des détails dans la mise en œuvre de l'association entre les sommets et ces collections, et de l'implémentation de ces collections elles-mêmes, selon qu'elles comprennent, comme élément de base, les deux sommets des arêtes, ou les arêtes comme objet, ou seulement les sommets voisins, ou encore dans le choix des types d'objets utilisés pour représenter les sommets et la liste de arêtes.
Les représentations de graphes par liste d'adjacence privilégient une approche plus centrée sur les sommets. Il existe de nombreuses implémentations possibles de listes d'adjacence :
- L'implémentation en Python préconisée par Guido van Rossum utilise une table de hachage pour associer, à chaque sommet du graphe, la table des sommets adjacents. Dans cette représentation, un sommet peut être représenté par tout objet qui peut être haché. Il n'y a pas de représentation explicite des arêtes en tant qu'objets[2].
- Le livre de Cormen et al.[3] propose une implémentation dans laquelle les sommets sont représentés par les numéros d'index. Leur représentation utilise un tableau indexé par les numéros des sommets, dans lequel la cellule du tableau correspondant pointe vers une liste chaînée des sommets voisins de ce sommet. Dans cette représentation, les éléments de la liste chaînée peuvent être interprétés comme des arêtes; cependant, ils ne stockent pas les informations complètes sur chaque arête mais seulement l'autre extrémité de l’arête et, dans les graphes non orientés, il y aura deux éléments de liste chaînée différents pour chaque arête (un dans les listes pour chacune des deux extrémités de l'arête).
- En programmation orientée objet, la structure dite liste d'incidence suggérée par exemple par Goodrich and Tamassia dans leur livre[4] possède des classes d'objets pour les sommets et pour les arêtes. Chaque objet sommet a une variable d'instance pointant vers une collection qui répertorie les objets qui sont les arêtes incidentes. À son tour, chaque arête pointe vers les deux objets sommet qui sont ses extrémités. Cette version de la liste d'adjacence utilise plus de mémoire que la version dans laquelle les sommets adjacents sont listés directement, mais l'existence d'objets arête explicites permet une flexibilité accrue, par exemple pour l'enregistrement d'informations supplémentaires sur les arêtes.
Opérations
L'opération principale effectuée par la structure de données de liste d'adjacence est de fournir une liste des voisins d'un sommet donné. En utilisant l'une des implémentations décrites ci-dessus, cela peut être effectué en temps constant par voisin. En d'autres termes, le temps total pour énumérer tous les voisins d'un sommet est proportionnel au degré du sommet.
On peut également utiliser des listes d'adjacence pour tester si une arête existe entre deux sommets donnés, mais cette représentation n'est pas efficace. Dans une liste d'adjacence dans laquelle les voisins de chaque sommet ne sont pas triés, le test de l'existence d'une arête peut être réalisée en temps proportionnel au degré de l'un des deux sommets donnés, en utilisant un parcours séquentiel des voisins de ce sommet. Si les voisins sont représentés comme un tableau trié, une recherche dichotomique peut être utilisée à la place, en temps proportionnel au logarithme du degré.
Compromis en espace
La principale alternative à la liste d'adjacence est la matrice d'adjacence, une matrice dont les lignes et les colonnes sont indexées par les sommets et dont les cellules contiennent une valeur booléenne qui indique si une arête existe entre les sommets correspondant à la ligne et la colonne de la cellule. Pour un graphe creux (un graphe qui n'a que peu d'arêtes), une liste d'adjacence est beaucoup plus efficace en espace qu'une matrice d'adjacence stockée dans un tableau) : la place requise par une liste d'adjacence est proportionnelle au nombre d'arêtes et de sommets du graphe, tandis que, pour une matrice d'adjacence stockées en tableau, l'espace est proportionnel au carré du nombre de sommets. Cependant, il est possible de stocker des matrices d'adjacence de manière plus efficace en espace, proche de l'espace linéaire linaire pris par une liste d'adjacence, en utilisant une table de hachage indexée par paires de sommets plutôt qu'un tableau. Comme chaque entrée de la matrice d'adjacence ne nécessite qu'un seul bit, elle peut être représentée d'une manière très compacte, en occupant seulement octets contigus en espace. En plus d'éviter le gaspillage d'espace, cette compacité encourage le principe de localité.
Cependant, pour un graphe creux, les listes d'adjacence nécessitent moins d'espace de stockage, car elles ne représentent pas les arêtes absentes. Ainsi, en utilisant une implémentation naïve par tableau sur un ordinateur 32 bits, une liste d'adjacence pour un graphe non orienté nécessite environ octets en place. Un graphe simple peut avoir au plus arêtes, si on autorise des boucles. Notons la densité du graphe. La représentation par liste d'adjacence occupe plus d'espace que la représentation matricielle si , donc si . Ainsi, un graphe doit être creux en effet pour justifier une représentation par liste d'adjacence.
Outre le compromis sur l'espace, les deux structures de données facilitent également différentes opérations. Trouver tous les sommets adjacents à un sommet donné dans une liste d'adjacence est aussi simple que le parcours de la liste. Avec une matrice d'adjacence, une ligne entière doit plutôt être parcourue, ce qui prend un temps . L'existence d'une arête entre deux sommets donnés peut être déterminée en temps constant dans une matrice d'adjacence, tout en exigeant un temps proportionnel au degré minimum des deux sommets de la liste d'adjacence.
Notes et références
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, [détail de l’édition]
- Guido van Rossum, « Python Patterns — Implementing Graphs »,
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, [détail de l’édition], section 22.1: Représentation des graphes.
- Michael T. Goodrich et Roberto Tamassia, Algorithm Design : Foundations, Analysis, and Internet Examples, John Wiley & Sons, , 708 p. (ISBN 0-471-38365-1).
Liens externes
- David Eppstein, « ICS 161 Lecture Notes: Graph Algorithms »,
- La bibliothèque logicielle Boost implémente une liste d'adjacence efficace.
- La bibliothèque Open Data Structures (in Java) contient une structure de liste d'adjacence : Open Data Structures - Section 12.2 - AdjacencyList: A Graph as a Collection of Lists.






