Lemme de van der Corput

Théorème — Soit ${\displaystyle \phi \in {\mathcal {C}}^{\infty }{\big (}[a,b]{\big )}}$ une fonction à valeurs réelles. On suppose que :

1. ${\displaystyle \left|\phi '\right|\geqslant 1}$ sur l'intervalle ${\displaystyle [a,b]}$ et ${\displaystyle \phi '}$ monotone, ou
2. il existe un entier ${\displaystyle k\geqslant 2}$ tel que ${\displaystyle \left|\phi ^{(k)}\right|\geqslant 1}$ sur ${\displaystyle [a,b]}$.

Alors il existe une constante ${\displaystyle c_{k}>0}$ indépendante de ${\displaystyle \phi }$ et de ${\displaystyle \lambda }$ telle que

${\displaystyle \left|\int _{a}^{b}\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant c_{k}\,\lambda ^{-1/k}\;.}$

On peut remarquer que l'hypothèse ${\displaystyle \phi \in {\mathcal {C}}^{\infty }{\big (}[a,b]{\big )}}$ est superflue ; en effet, il est suffisant que ${\displaystyle \phi }$ soit de classe ${\displaystyle {\mathcal {C}}^{k+1}{\big (}[a,b]{\big )}}$ pour que le théorème reste vrai.

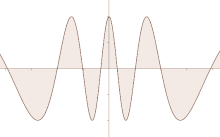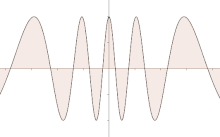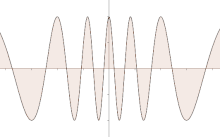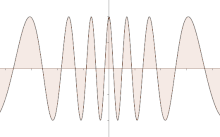
Une onde sans point stationnaire.

Une onde avec un point stationnaire en 0.

Bien que différents dans leur forme, le lemme de van der Corput et la méthode de la phase stationnaire reposent sur la même observation : les points stationnaires de la phase ${\displaystyle \phi }$ (c'est-à-dire ${\displaystyle \phi ^{(k)}(c)=0}$ ) influencent la décroissance de l'intégrale.

Pour comprendre cela intuitivement, on regarde la partie réelle de l'intégrale, à savoir

${\displaystyle \int _{a}^{b}\cos \left(\lambda \phi (x)\right)\,\mathrm {d} x\,.}$

Cette quantité mesure l'aire située entre la courbe définie par la fonction ${\displaystyle x\longmapsto \cos \left(\lambda \phi (x)\right)}$ et l'axe des abscisses. Il est clair que cette fonction, qui représente une onde, oscille de plus en plus rapidement quand le paramètre ${\displaystyle \lambda >0}$ tend vers l'infini. Si l'on suppose que la dérivée de la phase ne s'annule pas, on peut dire naïvement que les oscillations de l'onde ${\displaystyle x\longmapsto \cos \left(\lambda \phi (x)\right)}$ se comportent « de la même manière » à mesure que ${\displaystyle \lambda }$ devient grand. Il en résulte que l'aire positive et l'aire négative ont tendance à s'annuler mutuellement, ce qui fournit la décroissance.

Supposons à présent qu'il existe un point stationnaire de la phase, à savoir ${\displaystyle \phi ^{(k)}(c)=0}$. Alors dans un voisinage du point ${\displaystyle c}$, l'onde n'oscille que très peu, la courbe est en un sens plus « plate » dans cette zone. Il suit que les oscillations se compensent moins rapidement dans ce voisinage quand le paramètre ${\displaystyle \lambda }$ tend vers l'infini, ce qui a pour effet de ralentir la décroissance. Et le phénomène est d'autant plus marqué quand l'ordre du point stationnaire est élevé.

Nous allons faire la preuve par récurrence. Pour cela supposons que les hypothèses du premier cas soient satisfaites. Puisque ${\displaystyle \phi '}$ ne s'annule pas sur ${\displaystyle [a,b]}$, nous avons

${\displaystyle \int _{a}^{b}\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x=(\mathrm {i} \lambda )^{-1}\int _{a}^{b}{\frac {1}{\phi '(x)}}\,{\frac {\mathrm {d} }{\mathrm {d} x}}\left[\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\right]\,\mathrm {d} x=(\mathrm {i} \lambda )^{-1}\left[{\frac {\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}}{\phi '(x)}}\right]_{a}^{b}-\,(\mathrm {i} \lambda )^{-1}\int _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{\phi '(x)}}\right]\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x.}$

Puisque ${\displaystyle \phi '\geqslant 1}$ par hypothèse, nous avons

${\displaystyle \left|(\mathrm {i} \lambda )^{-1}\left[{\frac {\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}}{\phi '(x)}}\right]_{a}^{b}\right|=\left|(\mathrm {i} \lambda )^{-1}\left({\frac {\mathrm {e} ^{\mathrm {i} \lambda \phi (b)}}{\phi '(b)}}-{\frac {\mathrm {e} ^{\mathrm {i} \lambda \phi (a)}}{\phi '(a)}}\right)\right|\leqslant {\frac {2}{\lambda }}.}$

Ensuite, ${\displaystyle \phi '}$ étant supposée monotone, sa dérivée possède alors un signe constant. Il vient

${\displaystyle \left|(\mathrm {i} \lambda )^{-1}\int _{a}^{b}{\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{\phi '(x)}}\right]\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant \lambda ^{-1}\int _{a}^{b}\left|{\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{\phi '(x)}}\right]\right|\,\mathrm {d} x=\lambda ^{-1}\left|\left[{\frac {1}{\phi '(x)}}\right]_{a}^{b}\right|\leqslant {\frac {1}{\lambda }}.}$

Ceci termine le cas ${\displaystyle k=1}$.

On procède à présent par récurrence: on suppose que le cas ${\displaystyle k\geqslant 1}$ est connu et on suppose ${\displaystyle \left|\phi ^{(k+1)}\right|\geqslant 1}$ sur ${\displaystyle [a,b]}$. Désignons par ${\displaystyle c\in [a,b]}$ le point où la fonction ${\displaystyle \left|\phi ^{(k)}\right|}$ atteint son minimum. Distinguons deux cas:

• Si ${\displaystyle \phi ^{(k)}(c)\neq 0}$ alors on peut supposer sans perdre de généralités que ${\displaystyle \left|\phi ^{(k)}\right|\geqslant 1}$. Alors par récurrence

${\displaystyle \left|\int _{a}^{b}\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant c_{k}\,\lambda ^{-{\frac {1}{k}}}\leqslant c_{k}\,\lambda ^{-{\frac {1}{k+1}}},}$

pour tout ${\displaystyle \lambda \geqslant 1}$.

• Si ${\displaystyle \phi ^{(k)}(c)=0}$ alors on découpe l'intégrale comme suit :

${\displaystyle \int _{a}^{b}\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x=\int _{a}^{c-\delta }\ldots \,+\int _{c-\delta }^{c+\delta }\ldots \,+\int _{c+\delta }^{b}\ldots ,}$

où ${\displaystyle \delta >0}$ est un réel fixé suffisamment petit. On traite à présent chaque intégrale.

Pour tout ${\displaystyle x\in [c+\delta ,b]}$, nous avons

${\displaystyle \left|\phi ^{(k)}(x)\right|=\left|\phi ^{(k)}(x)-\phi ^{(k)}(c)\right|=\left|\int _{c}^{x}\phi ^{(k+1)}(y)\,\mathrm {d} y\right|=\int _{c}^{x}\left|\phi ^{(k+1)}(y)\right|\,\mathrm {d} y\geqslant (x-c)\geqslant \delta .}$

L'hypothèse de récurrence implique ainsi

${\displaystyle \left|\int _{c+\delta }^{b}\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant c_{k}\,(\delta \lambda )^{-{\frac {1}{k}}}\;;}$

un travail tout à fait similaire fournit

${\displaystyle \left|\int _{a}^{c-\delta }\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant c_{k}\,(\delta \lambda )^{-{\frac {1}{k}}}.}$

La dernière intégrale se majore brutalement :

${\displaystyle \left|\int _{c-\delta }^{c+\delta }\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant 2\delta .}$

Pour conclure, nous posons : ${\displaystyle \delta$ :=\lambda ^{-{\frac {1}{k+1}}}} . Nous obtenons ainsi la majoration finale :

${\displaystyle \left|\int _{a}^{b}\mathrm {e} ^{\mathrm {i} \lambda \phi (x)}\,\mathrm {d} x\right|\leqslant c_{k}\,\lambda ^{-{\frac {1}{k+1}}}+2\,\lambda ^{-{\frac {1}{k+1}}}+c_{k}\,\lambda ^{-{\frac {1}{k+1}}}=:c_{k+1}\,\lambda ^{-{\frac {1}{k+1}}}.}$

Si ${\displaystyle c=a}$ ou ${\displaystyle c=b}$, il suffit de découper l'intégrale en deux parties et de refaire exactement le même travail.

Ceci termine la preuve.