Lemme de Dickson

Une infinité de couples réels minimaux (x, y) (l'hyperbole noire) mais seulement cinq couples minimaux d'entiers positifs (rouge) vérifient xy ≥ 9.

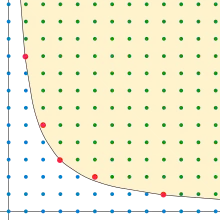
Soit ${\displaystyle K}$ un entier fixé, et soit ${\displaystyle S=\{(x,y)\mid xy\geq K\}}$ l'ensemble des couples de nombres dont le produit est au moins ${\displaystyle K}$. Lorsqu'il est défini sur les nombres réels positifs et muni de l'ordre produit, ${\displaystyle S}$ a une infinité d'éléments minimaux de la forme ${\displaystyle (x,K/x)}$, un pour chaque nombre positif ${\displaystyle x}$ ; cet ensemble de points est l'une des branches d'une hyperbole. Cependant, le lemme de Dickson ne concerne que les n-uplet d'entiers naturels, et sur les nombres naturels il n'y a qu'un nombre fini de couples minimaux. Chaque couple minimal ${\displaystyle (x,y)}$ d'entiers naturels vérifie ${\displaystyle x\leq K}$ et ${\displaystyle y\leq K}$, car si x était strictement supérieur à K alors (x − 1, y) appartiendrait aussi à S. Donc ${\displaystyle S}$ admet au plus ${\displaystyle K^{2}}$ éléments minimaux, un nombre fini[note 1].

Soit ${\displaystyle \mathbb {N} }$ l'ensemble des entiers naturels, soit n une constante fixe quelconque. On munit ${\displaystyle \mathbb {N} ^{n}}$ de l'ordre partiel produit, pour lequel ${\displaystyle (a_{1},a_{2},\dots ,a_{n})\leq (b_{1},b_{2},\dots b_{n})}$ si et seulement si, pour tout ${\displaystyle i}$, ${\displaystyle a_{i}\leq b_{i}}$. L'ensemble des n-uplets supérieurs ou égaux à un n-uplet particulier ${\displaystyle a=(a_{1},a_{2},\dots ,a_{n})}$ forme un orthant positif, de sommet ${\displaystyle a}$.

Avec cette notation, le lemme de Dickson peut être énoncé sous plusieurs formes équivalentes :

• pour toute partie non vide ${\displaystyle S}$ de ${\displaystyle \mathbb {N} ^{n}}$, l'ensemble des éléments minimaux de ${\displaystyle S}$ est fini et non nul[1] ;
• ${\displaystyle (\mathbb {N} ^{n},\leq )}$ est un bel ordre ;
• toute partie non vide ${\displaystyle S}$ de ${\displaystyle \mathbb {N} ^{n}}$ peut être couverte par un ensemble fini d'orthants positifs, dont les sommets appartiennent tous à ${\displaystyle S}$.

Dickson a utilisé son lemme pour prouver que, pour tout nombre donné ${\displaystyle n}$, il ne peut exister qu'un nombre fini de nombres parfaits impairs qui ont au plus ${\displaystyle n}$ facteurs premiers. Cependant, on ne sait pas s'il existe des nombres parfaits impairs.

La relation de divisibilité entre les entiers P-friables, entiers dont les facteurs premiers appartiennent tous à l'ensemble fini P, donne à ces nombres la structure d'un ensemble partiellement ordonné isomorphe à ${\displaystyle (\mathbb {N} ^{|P|},\leq )}$ . Ainsi, pour tout ensemble S de nombres P-friables, il existe un sous-ensemble fini de S tel que tout élément de S est divisible par l'un des nombres de ce sous-ensemble. Ce fait a été utilisé, par exemple, pour montrer qu'il existe un algorithme pour classer les coups gagnants et perdants à partir de la position initiale dans le jeu de Sylver (en), même si l'algorithme lui-même reste inconnu.

Les n-uplets ${\displaystyle (a_{1},a_{2},\dots ,a_{n})}$ dans ${\displaystyle \mathbb {N} ^{n}}$ sont en bijection avec les monômes ${\displaystyle x_{1}^{a_{1}}x_{2}^{a_{2}}\dots x_{n}^{a_{n}}}$ sur un ensemble de ${\displaystyle n}$ variables ${\displaystyle x_{1},x_{2},\dots x_{n}}$. Le lemme de Dickson peut être vu comme un cas particulier du théorème de la base de Hilbert indiquant que tout idéal polynomial engendré par des monômes est de type fini. En effet, Paul Gordan a utilisé cette reformulation du lemme de Dickson en 1899 dans le cadre d'une preuve du théorème de la base de Hilbert.

• Lemme de Gordan (en)