Lemme de Barbalat

Le lemme de Barbalat est un résultat d'analyse démontré par le mathématicien roumain Ion Barbălat en 1959[1]. Il est parfois utilisé dans l'étude des équations différentielles.

Énoncé

Lemme de Barbălat — Soit $f:\mathbb {R} \to \mathbb {R}$ une fonction uniformément continue dont l'intégrale sur $\mathbb {R}$ (au sens de Riemann) converge.

Alors ${\underset {x\to \pm \infty }{\lim }}f(x)=0$ .

Démonstration

Soit $\varepsilon >0$ . Par continuité uniforme de $f$ :

\exists \delta >0\quad \forall x,y\in \mathbb {R} \quad \left(|x-y|\leq \delta \implies |f(x)-f(y)|\leq \varepsilon \right)

Pour un tel $\delta$ , puisque l'intégrale de $f$ sur $\mathbb {R}$ converge :

\exists A\in \mathbb {R} \quad \forall x\in \mathbb {R} \quad \left(|x|\geq A\implies \left|\int _{x}^{x+\delta }f(t)\,\mathrm {d} t\right|\leq \varepsilon \delta \right)

On en déduit :

\forall x\in \mathbb {R} \quad \left(|x|\geq A\implies \delta |f(x)|=\left|\int _{x}^{x+\delta }f(x)\,\mathrm {d} t\right|\leq \int _{x}^{x+\delta }|f(x)-f(t)|\,\mathrm {d} t+\left|\int _{x}^{x+\delta }f(t)\,\mathrm {d} t\right|\leq 2\varepsilon \delta \right)

donc

\forall x\in \mathbb {R} \quad \left(|x|\geq A\implies |f(x)|\leq 2\varepsilon \right)

Contre-exemple

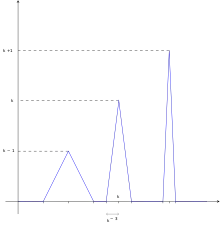
Le triangle centré en

k

est d'aire

{\frac {1}{k^{2}}}

L'hypothèse d'uniforme continuité est essentielle, même si la fonction est positive. En effet, si l'on considère la fonction affine par morceaux $f$ définie par :

\forall k\geqslant 2\quad \forall x\in \left[k-{\frac {1}{k^{3}}},k\right]\quad f(x)=k^{4}\left(x-k+{\frac {1}{k^{3}}}\right){\text{ et }}\forall x\in \left[k,k+{\frac {1}{k^{3}}}\right]\quad f(x)=-k^{4}\left(x-k-{\frac {1}{k^{3}}}\right)

et $f$ est nulle ailleurs, la fonction $f$ est bien intégrable, car : $\int _{-\infty }^{+\infty }|f(t)|\,\mathrm {d} t=\sum _{k=1}^{+\infty }{\frac {1}{k^{2}}}<+\infty$ .

Or, $f$ ne tend pas vers $0$ en $+\infty$ (elle n'est même pas bornée).

Références

I. Barbălat, « Systèmes d’équations différentielles d’oscillations non linéaires », Rev. Roumaine Math. Pures Appl., vol. 4,‎ 1959, p. 267-270.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.