Instabilité géométrique

Une instabilité est une modification soudaine de la réponse d’une structure soumise à une charge statique augmentant progressivement. Lors d’une instabilité, les structures donnent l’impression de se dérober sous leurs charges.

Exemple 1

Fig.2, sous de faibles charges.

Fig.3, à la charge critique.

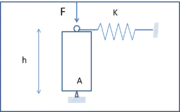
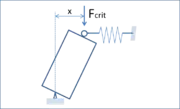
À considérer un poteau stabilisé par un ressort en tête (Fig. 2). Il est relativement massif et est soumis à une force de compression axiale F croissante. Pour de faibles valeurs de F, la déformation du poteau est axiale. Lorsque F atteint une valeur dite charge critique, le ressort de tête s’écrase et l’ensemble prend la déformation de la fig. 3.

L’équilibre moment calculé au pied du poteau (point A) donne la charge critique :

${\displaystyle F_{\mathrm {crit} }*x-K*x*H=0}$

soit :

${\displaystyle F_{\mathrm {crit} }=K*H}$

où K est la raideur du ressort et H la hauteur du poteau.

Remarques :

• la charge critique dépend des paramètres de la géométrie (ici K et H) et pas de la qualité des matériaux (que l’ensemble soit en acier, en béton ou en un autre matériau, F_crit est la même). Il s'agira d'instabilité géométrique ;
• à la charge critique, nous assistons à une bifurcation c’est-à-dire à un changement de mode de déformation.

Exemple 2

Fig. 4, sous de faibles charges.

Fig. 5, à la charge critique.

Déformation de rails sous l'effet du soleil.

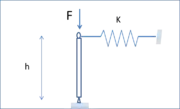
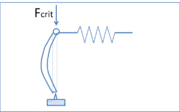
À considérer la même structure que précédemment mais avec un poteau beaucoup plus élancé (par exemple, parce qu’il a une section plus faible), ou un ressort beaucoup plus raide (Fig.4). Pour de faibles valeurs de F, la déformation est une compression axiale du poteau. Lorsque F atteint une valeur dite charge critique, le poteau se déforme dans le plan perpendiculaire à son axe (Fig. 5). Il est dit que le poteau « flambe ». La charge critique est donnée par la formule d’Euler :

${\displaystyle F_{\mathrm {crit} }={\frac {\pi ^{2}\cdot E\cdot I}{H^{2}}}}$

où :

• E = le module de Young du matériau ;
• I = l'inertie du poteau ;
• H = la hauteur du poteau.

Remarque : à la charge critique, la déformation dans le poteau ne dépend pas du matériau utilisé. Divisons F_crit par la section et par le module de Young. Une déformation critique ${\displaystyle {\varepsilon }_{\mathrm {crit} }={\frac {\pi ^{2}\cdot I}{A\cdot H^{2}}}}$ est obtenue, (où A est la section du poteau) dépendant seulement de la géométrie.

D’une façon générale :

• c’est la plus petite des charges critiques des exemples 1 et 2 qui déterminera le mode d’instabilité réel de la structure[2] ;
• les structures élancées[3] sont plus sensibles à l’instabilité que les structures massives. En ce sens, les constructions métalliques sont plus souvent concernées que les constructions en béton ;
• les charges peuvent être d’origine mécanique ou thermique ;
• les charges à l’origine des instabilités sont presque toujours des forces de compression[4].

Exemple 3

Statue en bronze de Charlie Chaplin à Vevey (Suisse).

D’une manière générale, on essaye d’éviter les instabilités et leurs effets néfastes. Voici cependant un exemple d’utilisation positive.

L’acteur de cinéma Charlie Chaplin se promène souvent avec l’aide d’une canne en jonc. Au départ, celle-ci est rectiligne. Quand l’acteur s’appuie légèrement, elle reste rectiligne et soutient son effort. S’il s’appuie plus fortement, elle prend une forme courbe et s’avère incapable de soutenir l’acteur. Cela peut aller jusqu’à la chute pour la plus grande joie des petits et des grands. L’acteur a ainsi popularisé une forme d’instabilité, c'est-à-dire que lorsque la force appliquée (ici la poussée de l’acteur) atteint une certaine valeur, la structure (ici la canne) change subitement de géométrie et devient incapable de soutenir la charge.

L'instabilité géométrique est le terme général couvrant le phénomène. Divers termes plus précis permettent de qualifier le comportement des structures :

• bifurcation : une bifurcation intervient lorsqu'une petite augmentation des charges produit un changement majeur dans le mode de déformation de la structure. C’est le comportement théorique pour l’instabilité d’une structure parfaite (sans défaut de forme). Voir fig. 3 et 5 ;
• charge critique : charge correspondant au début de l’instabilité ;
• claquage : à sa charge critique, la structure passe brusquement d’un état d’équilibre à un autre qui lui est fortement éloigné. Le chemin parcouru entre ces deux équilibres stables passe par des positions d’équilibre instable. Il s'agit d’un mouvement dynamique. Les claquages concernent principalement les arcs et les coques ;

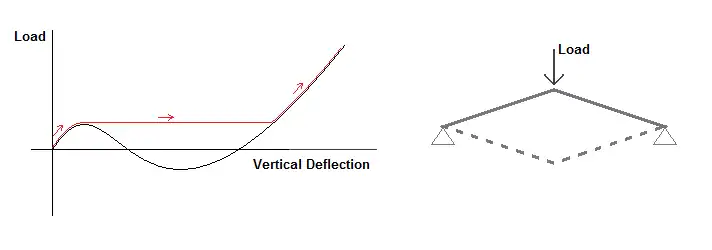
• comportement post-critique : comportement de la structure si elle est chargée au-delà de sa charge critique ;
• déversement : le déversement est une instabilité affectant les poutres et surtout les poutrelles utilisées en construction métallique. Un moment de flexion sollicitant une poutre correspond à une traction dans une semelle et à une compression dans l’autre. Si la semelle comprimée atteint sa charge critique et flambe latéralement, toute la poutre se déverse comme si elle était soumise localement à un moment de torsion ;
• divergence : une divergence se produit pour les structures possédant des défauts de forme. Lors de la mise en charge, ce défaut croit perpendiculairement à l’axe (ou au plan) de référence de la structure. La forme de la structure diverge de plus en plus de la forme au repos ;
• flambement : le flambage ou flambement est la bifurcation d'un poteau soumis à un effort normal de compression atteignant la charge critique. Il fléchit et se déforme dans une direction perpendiculaire à l'axe de compression. Voir fig. 5 ;
• instabilité élastique ou plastique : une instabilité est dite élastique quand elle se produit pour des contraintes inférieures à la limite élastique du matériau. Elle est dite plastique si ces contraintes dépassent cette limite élastique ;
• mode de flambement : forme que prend la structure lorsque l’instabilité commence ;
• voilement : le voilement (ou cloquage) est une instabilité des plaques et des coques qui se manifeste par des boursoufflures perpendiculaires à la plaque ou à la coque.

En dehors de quelques cas simples traités « manuellement » (comme l’exemple 1), les calculs de charge critique sont souvent longs et complexes. L’aide des programmes informatique est souvent indispensable. À la charge critique, un léger surcroît de charge induit des déplacements très importants. En d’autres termes, la raideur tangente s’annule[5]. On utilisera donc des méthodes mathématiques permettant d’isoler les conditions d’annulation de la raideur[6], ou des méthodes exprimant la conservation de l'énergie[7].

Fig.6, mode théorique d'instabilité d'un cylindre chargé axialement.

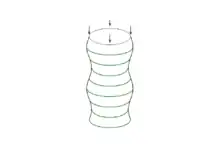
Les études théoriques donnent la charge critique des structures considérées comme parfaites (c'est-à-dire des poutres bien droites et de section constante, des plaques uniformément planes, etc.). Les structures réelles sont cependant loin de cette perfection et présentent des défauts de géométrie (variation locale de l’épaisseur, ovalisation, distance entre la ligne neutre théorique et réelle, discontinuité au droit des soudures, etc.). Ces défauts influencent la charge critique. Certaines structures sont particulièrement sensibles à la présence d’un défaut de forme. C’est, par exemple, le cas des cylindres chargés selon leur axe[8].

Pour éviter une instabilité, le constructeur dispose de plusieurs moyens :

• diminuer la taille des imprécisions et des défauts de forme ;
• augmenter les épaisseurs, ce qui augmente d’autant le poids de la structure ;
• prévoir des raidisseurs[9] (cas des plaques et coques, par exemple pour les réservoirs métalliques) ;
• prévoir des contreventements (cas fréquent en construction métallique, par exemple pour les pylônes en treillis supportant les lignes électriques).

L’instabilité des colonnes idéales comprimées a été découverte par Leonhard Euler en 1744. En son honneur, la formule correspondante a gardé son nom[10]. En 1892, le mathématicien Alexandre Liapounov introduit la notion de stabilité de Lyapunov pour les systèmes dynamiques. Ce théorème très général couvre également le cas spécifique des systèmes statiques[11].

Ces dernières années, les structures sont de plus en plus légères et élancées. Les développements informatiques permettent aux constructeurs de les utiliser au plus près de leur charge critique[12].

La stabilité des constructions exige de se prémunir contre les diverses instabilités possibles. Plusieurs règlements donnent des critères d’acceptation pour les structures concernées :

• les Eurocodes développés par le Comité européen de normalisation (CEN), et plus spécifiquement l’Eurocode 3 : Calcul des structures en acier (EN 1993)[13] ;
• voilement des coques – Recommandations de la Convention européenne de la construction métallique (CECM)[14] ;
• (en) American Society of Mechanical Engineers (ASME) : Boiler and pressure vessel code, section VIII division 1 : Design and fabrication of pressure vessels.

: document utilisé comme source pour la rédaction de cet article.

• « Flambage élastique et plastique des coques minces », cours de l’Institut pour la Promotion des Sciences de l’Ingénieur (IPSI), Paris, avril 1982
• « Flambage des coques minces », cours de l’Institut pour la Promotion des Sciences de l’Ingénieur (IPSI), Paris, avril 1986
• Charles Massonnet, « Résistance des Matériaux », Sciences et Lettres - Liège - 1960
• Elie Absi, « Grandes Déformations et Instabilité des Structures », in Annales de l’Institut Technique du Bâtiment et des Travaux Publics, n^o 469, novembre 1988, Paris
• S. Timoshenko, « Théorie de la stabilité élastique », Librairie Polytechnique Béranger, Paris et Liège
• (en) J.E. Gordon, « Structures or why things don’t fall », Penguin Books, 1978
• (en) David Bushnell, « Buckling of shells – Pitfall for designers », Lockheed Palo Alto Research Laboratory, Palo Alto, Calif. ; in AIAA J., vol. 19, n^o 9, septembre 1981