Immersion (mathématiques)

En géométrie différentielle, une immersion est une application différentiable d'une variété différentielle dans une autre, dont la différentielle en tout point est injective.

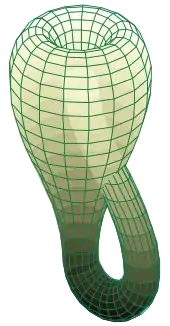
Immersion — nécessairement non injective — de la bouteille de Klein dans R³.

Soient V et W deux variétés et f une application différentiable de V dans W.

On dit que f est une immersion si pour tout x appartenant à V, le rang de l'application linéaire tangente Tf(x) est égal à la dimension de V.

On la différencie :

de la submersion (le rang de Tf(x) est égal à la dimension de W) ;
du plongement (en plus d'être une immersion, f est un homéomorphisme de V sur f(V)).

Théorème

Soit $U$ une partie ouverte de ${\mathbb {R}}^{p}$ , $f$ une immersion injective de $U$ dans ${\mathbb {R}}^{n}$ . On suppose que l'application $f^{-1}$ de $V=f(U)$ sur $U$ est continue. Alors $V$ est une variété de ${\mathbb {R}}^{n}$ de dimension $p$ [1].

références

Jacques Dixmier, Cours de mathématiques du premier cycle : deuxième année : exercices, indications de solutions, réponses, Gauthier-Villars, 1977 (ISBN 2-04-015715-8 et 978-2-04-015715-9, OCLC 23199112), p. 195

Article connexe

Théorème d'immersion de Whitney (en)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.