Graphe de Harborth
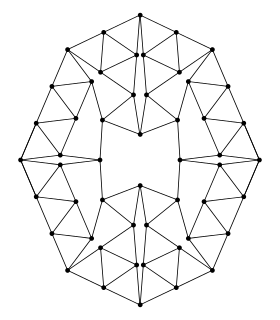
Le graphe de Harborth est, en théorie des graphes, un graphe 4-régulier possédant 52 sommets et 104 arêtes. C'est un graphe allumette donc c'est à la fois un graphe distance-unité et un graphe planaire. Il s'agit du plus petit graphe allumette 4-régulier connu et il fut découvert par Heiko Harborth en 1986[1]. Si sa minimalité n'est toujours pas prouvée, on sait en revanche qu'il n'existe pas de graphe allumette 5-régulier[2].
| Graphe de Harborth | |
| |
| Nombre de sommets | 52 |
|---|---|
| Nombre d'arêtes | 104 |
| Distribution des degrés | 4-régulier |
| Rayon | 6 |
| Diamètre | 9 |
| Maille | 3 |
| Automorphismes | 4 (Z/2Z×Z/2Z) |
| Nombre chromatique | 3 |
| Indice chromatique | 4 |
| Propriétés | Allumette Distance-unité Planaire Eulérien |
Propriétés
Propriétés générales
Le diamètre du graphe de Harborth, l'excentricité maximale de ses sommets, est 9, son rayon, l'excentricité minimale de ses sommets, est 6 et sa maille, la longueur de son plus court cycle, est 3. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 4-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 4 arêtes.
En 2006, Eberhard H.-A. Gerbracht démontra que c'était un graphe rigide[3].
Coloration
Le nombre chromatique du graphe de Harborth est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.
L'indice chromatique du graphe de Harborth est 4. Il existe donc une 4-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du 52-graphe de Harborth est un groupe abélien d'ordre 4 isomorphe à Z/2Z×Z/2Z, le groupe de Klein.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Harborth est :
Voir aussi
Liens internes
Liens externes
- (en) Eric W. Weisstein, Harborth Graph (MathWorld)
Références
- Harborth, H. "Match Sticks in the Plane." In The Lighter Side of Mathematics. Proceedings of the Eugéne Strens Memorial Conference of Recreational Mathematics & its History. Calgary, Canada, July 27-August 2, 1986 (Eds. R. K. Guy and R. E. Woodrow). Washington, DC: Math. Assoc. Amer., pp. 281-288, 1994.
- Peterson, I. "Mathland: Matchsticks in the Summer." August 1996. http://www.maa.org/mathland/mathland_8_12.html
- Gerbracht, E. H.-A. "Minimal Polynomials for the Coordinates of the Harborth Graph." Oct. 5, 2006. https://arxiv.org/abs/math.CO/0609360.



