Graphe allumette
En mathématiques, plus particulièrement en théorie des graphes, un graphe allumette est un graphe connexe dont il est possible de donner une représentation dans le plan en représentant toutes les arêtes par des segments de même longueur et ne se croisant jamais.
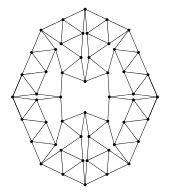
Le graphe de Harborth est un exemple de graphe allumette.
Un graphe allumette est donc à la fois un graphe planaire et un graphe distance-unité[1]. La réciproque est fausse : le graphe de Moser, qui est à la fois un graphe planaire et un graphe distance-unité, n'est pas un graphe allumette.
Exemples
- Tous les cycles ;
- Le graphe roue W7 (c'est le seul graphe roue à être distance-unité) ;
- Le graphe de Harborth.
Références
- Jean-Paul Delahaye, « Les graphes-allumettes », Pour la Science, no 445, (lire en ligne)
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.