Géomécanique
La géomécanique est l’outil mathématique de la géotechnique ; elle synthétise la mécanique des sols, la mécanique des roches, l’hydraulique souterraine et une partie de la sismique[1].
Lors d’études géotechniques pour aménager et/ou exploiter la subsurface terrestre : projeter, construire et entretenir un ouvrage ; assurer la stabilité d’un talus de remblais ou de déblais, d’une excavation souterraine, d’un soutènement, estimer celle d’un versant naturel ; éviter la rupture et limiter le tassement d’une fondation d’ouvrage ; estimer le débit d’un puits, d’un drain, d’une fouille à épuiser... on doit poser des problèmes de géomécanique et les résoudre par le calcul ; ils concernent la déformation ou le déplacement du géomatériau, sol, roche et/ou eau, sous l’action de la gravité à laquelle peuvent s’associer des efforts spécifiques, induits par un événement naturel ou par la mise en œuvre du sous-sol d'un site de construction ; ce sont généralement des charges de remblais ou de fondations, des décharges de galeries ou de déblais, des pressions hydrostatiques ou de courant…
Définition
La géomécanique que l’on confond généralement avec la géotechnique, est son outil mathématique, nécessaire mais insuffisant ; la géologie - géologie structurale, géomorphologie, géodynamique - et la géophysique – électrique, sismique - doivent en effet lui fournir les modèles de formes, d'états et de comportements des massifs de géomatériaux réels étudiés, dont elle a besoin pour fixer les conditions initiales - les états - et aux limites - les formes - de ses calculs analytiques ou numériques de comportements schématiques et figés de milieux virtuels, applications de théories fondées sur des « lois » linéaires, déterministes - Hooke, Coulomb, Terzaghi, Darcy.
En pratique géotechnique, la géomécanique, la géologie et la géophysique sont indissociables, interdépendantes et complémentaires. Les moyens de prospection géophysiques permettent une "visualisation" du sous-sol qui précisent les coupes géologiques - morphologie et structure : les modèles de forme obtenus par sondages et tomographies sismiques sont indispensables à la géomécanique pour valider ses modèles spécifiques de calculs.
Les milieux
Pour le géomécanicien, un sol est un géomatériau meuble dont les paramètres mécaniques ont des valeurs faibles ; ce peut être une grave alluviale aussi bien qu’un granite arénisé... Il donne par contre au mot roche un sens beaucoup plus proche du sens commun en appelant roche un géomatériau compact et dur, dont les paramètres ont des valeurs élevées. L’état et le comportement mécanique d'un sol dépendent essentiellement de sa teneur en eau ; ceux d’une roche, de son degré d’altération, de fissuration et de fracturation.
Les milieux virtuels que manipule la géomécanique sont continus, immuables, homogènes, isotropes, libres, parfois non pesants (sans contrainte) ; ce sont les modèles de géomatériaux naturels, tangibles, discontinus, variables, hétérogènes, anisotropes, contraints, pesants..., réduits à quelques paramètres caractéristiques utilisés dans les calculs. On peut retenir :
- Sols : géomatériaux meubles, plus ou moins frottants et/ou plastiques dont la cohésion est faible. Elle diminue jusqu’à disparaître (liquéfaction) par accroissement de la teneur en eau.
- Paramètres caractéristiques : densité, teneur en eau, angle de frottement, cohésion...
- Roches : géomatériaux compacts et durs dont la résistance à la compression simple est supérieure à quelques MPa. Elle diminue et/ou disparaît par altération physique (hydratation), chimique (dissolution) et/ou mécanique (fragmentation).
- Paramètres caractéristiques : vitesse sismique, module d’élasticité, résistances à la compression, à la traction, au cisaillement...
Les disciplines géomécaniques
L’étude du comportement mécanique des formations meubles de couverture, les sols, ressortit à la mécanique des sols, la plus ancienne, la plus connue et la plus pratiquée de ces disciplines parce que la plupart des problèmes géotechniques se posent pour la mise en œuvre de ces formations lors de la construction de la plupart des ouvrages de subsurface ; la mécanique des roches en est l’adaptation aux études du comportement mécanique des formations dures plus ou moins profondes. La distinction de la mécanique des sols et de la mécanique des roches qui manipulent les mêmes théories selon des démarches analogues est historique et pratique : depuis le XIXe siècle : mécanique des sols aux terrassements et au bâtiment ; depuis le milieu du XXe siècle : mécanique des roches aux grands ouvrages - barrages, galeries…. L’étude de l’écoulement de l’eau dans le sous-sol perméable sous l’effet de la gravité et/ou par pompage ressortit à l’hydraulique souterraine.
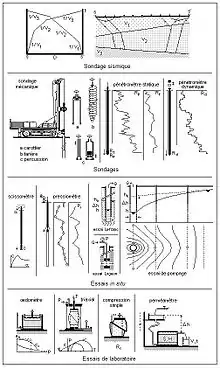
Ces trois disciplines ont pratiquement les mêmes moyens de recueil des données de terrain – sondages, essais in situ (pénétromètre, pressiomètre...) et de laboratoire (œdomètre, triaxial...), les mêmes modèles de formes géométriques ou numériques, très schématiques - deux dimensions, droites, cercles…, construits sur des données locales, peu nombreuses et peu précises - valeurs de quelques paramètres censés caractériser le milieu virtuel représentant le géomatériau (densité, angle de frottement, cohésion, perméabilité…) -, les mêmes méthodes de calcul - intégration d’équations de champs très complexes dont, au mieux, on ne connaît que les équipotentielles de surface. Cela impose des conditions initiales et aux limites simplistes à des calculs plus ou moins compliqués, réduits in fine à des formules biunivoques - à une seule et même cause (effort, pression, contrainte…) correspond toujours strictement un seul et même effet (déplacement, déformation, écoulement…) -, dont les résultats ne sont que des ordres de grandeur. Depuis le XVIIIe siècle, ces résultats ont été successivement obtenus par des méthodes de calcul graphiques, puis trigonométriques, analytiques et enfin numériques que, maintenant, on utilise plus ou moins conjointement.
Démarche de la géomécanique
En pratique, selon la nature et la structure du sous-sol du site étudié et à partir de données obtenues sur le terrain et/ou au laboratoire par la géologie, la sismique, les sondages et les essais, la démarche de la géomécanique consiste à bâtir un modèle de forme géométrique ou numérique, à imposer au milieu virtuel dont il est constitué le modèle de comportement correspondant au problème géotechnique posé, puis à appliquer la méthode de calcul adéquate pour obtenir le résultat attendu.
Le modèle de forme doit être assez simple pour que sa manipulation mathématique soit commode et efficace : l’espace est à deux dimensions dans le plan des contraintes principales ; les figures sont les coupes perpendiculaires selon l’axe de la contrainte moyenne ; les limites sont généralement des segments de droite et des arcs de cercle, plus rarement des arcs d’ellipse, de spirale logarithmique, de cycloïde... ; l’extension des parties non limitées des figures est infinie. Le milieu virtuel est continu, homogène, isotrope, libre de contraintes, confiné, immuable, réduit à des paramètres de résistance, perméabilité, compressibilité… mesurés au moyen d’essais plus ou moins normalisés in situ ou sur échantillons. Le géomatériau est constitué entre autres de matière minérale et d’eau ; si on néglige l’eau dans son comportement, le milieu est monophasique ; si on ne la néglige pas, il est biphasique.
Son modèle de comportement est généralement une relation cause-effet déterministe : une action mécanique extérieure – force, pression – produit une réaction du modèle – déplacement, déformation – et/ou du milieu – contrainte, rupture, écoulement… Dans la plupart des cas, on calcule la grandeur de l’effet selon l’"intensité" de la cause par une formule biunivoque issue d’un calcul d’intégration théorique : on obtient l’état statique final que le modèle de forme atteint instantanément à partir de son état statique initial. Ainsi, un événement géomécanique est l’effet instantané d’une action isolée intemporelle ; il est déterminé par une "loi" qui contraint l’action ; théoriquement, on peut le reproduire à l’identique n’importe où et n’importe quand ; le milieu virtuel dans lequel il se manifeste est transformé instantanément ; il n’évolue pas.
Les milieux, les modèles de forme et de comportement de la géomécanique doivent être compatibles avec ceux de la géologie, mais ils ne peuvent manifestement pas l’être : la lithologie indique que les roches sont bien plus diverses et variées que les milieux de la géomécanique, réduits à trois "sols" types, des sols meubles – sable (frottant) et argile (plastique) éventuellement mêlés en quantités variables – et des roches dures – quelle qu’en soit la nature (élastique ?) ; la géologie structurale et la géomorphologie indiquent que les formes naturelles des formations rocheuses ne peuvent jamais être réduites à des formes géométriques simples : aucun géomatériau n’est homogène et isotrope, indéfiniment identique à lui-même vers la profondeur et latéralement ; la surface du sol, d’une strate, d’une faille n’est jamais plane et ne fait jamais un angle constant par rapport à un repère horizontal ou vertical ; aucun pli n’est cylindrique… ; la géodynamique indique que le géomatériau altérable n’est pas immuable, qu’il ne réagit pas instantanément et de façon convenue aux diverses actions auxquelles il peut être soumis…
Ainsi, la démarche géomécanique strictement déterministe conduit bien à un résultat mathématique précis, mais pour l’obtenir, il a fallu schématiser la réalité géologique de sorte qu’il n’a qu’une valeur pratique d’ordre de grandeur ; on le minore donc au moyen d’un coefficient de sécurité afin que l’ouvrage projeté et construit sur sa base soit solide, propre à sa destination et le reste sans subir de dommage ; pour ne pas surdimensionner l’ouvrage, ce coefficient doit être aussi petit que possible, mais on ne sait pas comment y parvenir par le calcul ; il reste donc toujours ce que Verdeyen appelait une poudre de perlimpimpin.
Les théories
Au moyen de courbes graphiques temps-effort-déformations, l’analyse qualitative de ce comportement complexe est possible mais insuffisante pour obtenir un résultat particulier ; pour le faire mathématiquement, il faut analyser chaque étape du comportement – élasticité, plasticité, rupture - au moyen d’une théorie trop spécifique d’un problème type pour être généralisée sans devoir recourir à des développements compliqués et mal fondés ; ainsi, dans l’état actuel de nos connaissances mais sans doute par essence, une théorie unitaire de la géomécanique ne peut pas être formulée : c’est ce que pensent la plupart des praticiens (Collin, Fellenius, Terzaghi…), mais pas toujours les théoriciens (Poncelet, Boussinesq, Caquot…) qui s’efforcaient d’y parvenir, vainement jusqu’à présent, sauf peut-être Ménard avec la théorie du pressiomètre qui ne s’applique en fait qu’à l’usage de cet appareil et à la méthode de calculs correspondante.
Or les théories fondamentales de la géomécanique sont circonstancielles : elles ont été formulées indépendamment les unes des autres par leurs auteurs respectifs qui étaient des ingénieurs praticiens pour résoudre des problèmes techniques très spécifiques que posaient la conception et la construction d’objets et/ou d’ouvrages nouveaux, en s’appuyant sur des observations de phénomènes qu’ils supposaient influents et sur des expériences simples, de courtes durées, que la géomécanique appelle essais. La formulation linéaire de ces théories est une schématisation qui correspond à de courts intervalles de définition, car les moyens d’expérimentation et de calcul dont ils disposaient n’en permettait pas davantage, et la simplicité relative des ouvrages qu’ils devaient construire n’en exigeait pas plus ; elles ont ensuite facilité les développements des théories ; elles facilitent toujours nos calculs pratiques.
Les essais que l’on réalise pour mesurer les paramètres des matériaux du sous-sol d’un site, in situ au cours de sondages ou au laboratoire sur des échantillons sont en fait des expériences de validation de ces théories… dont les résultats ne sont pas toujours très convaincants, car l’alignement des points représentatifs des mesures sur un repaire cartésien n’est obtenu que par un lissage plus ou moins étendu.
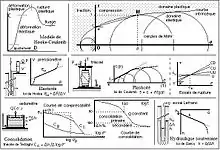
Les théories de l’élasticité (Hooke), de la plasticité et de la rupture (Coulomb) s’appliquent en continuité à la déformation d’un milieu monophasique imperméable soumis à un effort croissant ; ainsi, dans le modèle élasto-plastique de Hooke/Coulomb, il subit successivement une déformation élastique, un glissement et une rupture plastiques. La théorie de la consolidation (Terzaghi) s’applique à la déformation d’un milieu perméable biphasique soumis à un effort constant. La théorie de l’hydraulique souterraine (Darcy) s’applique à l’écoulement de l’eau dans un milieu indéformable perméable soumis à un gradient de pression.
L’élasticité
La théorie géomécanique de l’élasticité est fondée sur la loi de Hooke, proportionnalité du rapport effort (C)/déformation (D) exprimée par le module d’Young (E) du milieu, constant si l’effort croissant maximal est assez faible pour que la déformation soit strictement réversible quand il décroît : E ≈ C/D. Elle peut s’appliquer à certains comportements mécaniques des sols et des roches ; en particulier, pour les fondations et les galeries, on s’efforce toujours à faire en sorte que sous l’effet des charges qu’on lui impose, les déformations du géomatériau ne sortent pas du domaine élastique.
Sans en donner une définition claire, les géomécaniciens l’appliquent à un milieu pseudo-élastique et définissent autant de modules "élastiques" différents entre eux et du module d’Young, que d’appareils d’essais et de méthodes de calcul dont ils disposent, ce qui peut entraîner de dangereuses confusions pratiques. Plusieurs essais permettent de mesurer de tels modules ; l’essai in situ au pressiomètre est le plus courant et le plus simple d’entre eux ; au laboratoire, on peut utiliser la compression simple ou le triaxial.
Elle s’applique aussi à la propagation des ondes sismiques qui imposent de faibles contraintes à un massif de géomatériau, caractérisé par sa vitesse (V).
La plasticité et la rupture
La théorie de la plasticité et de la rupture est fondée sur la loi de Coulomb ; elle concerne plus particulièrement les matériaux sablo-argileux meubles, monophasiques.
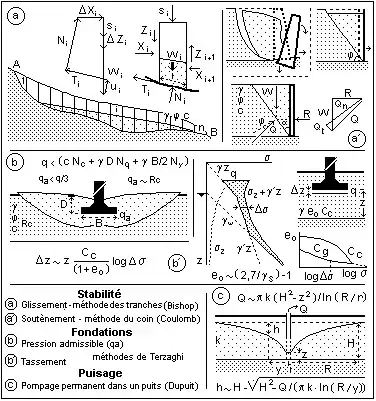
Coulomb a établi la formule linéaire permettant de prévoir la rupture par cisaillement d’un géomatériau meuble sous l’effet conjugué d’une traction (T) et d’une compression (N) : T = c + N*tgφ, dans laquelle c (cohésion) et φ (angle de frottement) sont les paramètres constants caractéristiques du matériau et de sa compacité – en fait, c et φ dépendent de N et la courbe représentative de cette fonction est une demi-parabole dite courbe intrinsèque du matériau que l’on convertie en droite par lissage. Si le point représentatif (M) de l’état du matériau caractérisé par un couple c/φ est situé sous la courbe, c et φ sont virtuels, le matériau se déforme élastiquement ; s’il est sur la courbe, il est à sa limite d’adhérence au-delà de laquelle à la fois naît le glissement et se produit la rupture ; s’il est au-dessus de la courbe, c disparaît et une partie de φ persiste, il glisse plastiquement.
Les calculs théoriques ne peuvent utiliser que des milieux purement frottants dont la cohésion est nulle ou des milieux purement cohérents dont l’angle de frottement est nul ; il n'existe évidemment pas de tels géomatériaux réels. En pratique, si c est petit devant N*tgφ, le matériau est dit frottant ; si c est grand, le matériau est dit cohésif. Si c est très grand, la loi de Coulomb n’est plus pertinente ; on caractérise le matériau dur et cassant - roches et sols résistants - par sa résistance à la compression simple Rc, paramètre pratique très facile à mesurer au moyen d’une simple presse ; on admet que Rc ≈ 2 c.
Plusieurs essais de terrain et de laboratoire permettent de mesurer la cohésion et l’angle de frottement d’un géomatériau. Au laboratoire, selon que l’on compacte ou non le matériau des éprouvettes, qu’on le charge plus ou moins rapidement et que l’on draine ou non, on réalise des essais plus ou moins consolidés (C), drainés (D), lents qui donnent respectivement des couples c/φ différents : CD (consolidé, drainé ou lent), CU (consolidé, non drainé ou rapide), UU (non consolidé, non drainé ou rapide), U ; en pratique, on maîtrise mal le pilotage de l’essai, matériau plus ou moins drainé et consolidé, effort plus ou moins lent. L’essai par cisaillement plan à la boîte de Casagrande est le plus courant et le plus simple ; il donne des couples c/φ génériques – CD ou UU -, largement suffisants pour les applications courantes ; l’essai au triaxial permet de réaliser tous les types d’essais ; les manipulations sont très longues, très compliquées et les résultats obtenus sont rarement nécessaires en pratique.
La consolidation
La théorie de la consolidation a été proposée par Terzaghi ; elle concerne les matériaux sablo-argileux meubles biphasiques.
Sous l’action constante de son propre poids dans la nature ou sous celle d’une charge extérieure, un tel matériau se consolide de plus en plus à mesure que le temps passe : son indice des vides et sa teneur en eau diminuent, sa densité et sa résistance mécanique augmentent, sa perméabilité diminue ; le phénomène naturel est la partie mécanique de la diagenèse qui transforme les sédiments meubles en roches sédimentaires à l’échelle du temps géologique ; le phénomène induit par une charge extérieure verticale comme le poids d’un ouvrage est un tassement à l’échelle du temps humain. À l’inverse, si l’action est une décharge, l’indice des vides et la teneur en eau du matériau augmentent, sa densité et sa résistance mécanique diminuent ; le phénomène naturel est la partie mécanique de l’altération qui transforme les roches dures en altérites meubles ; le phénomène induit est un gonflement – talus de déblais, fond de fouille, parois de galerie… ; dans certaines conditions, le géomatériau peut alternativement tasser en se desséchant et gonfler en s’hydratant. La déformation est dite pseudo-élastique : le rapport contrainte/déformation n’est pas constant comme le module d’Young du comportement élastique linéaire ; il dépend de la pression interstitielle et de ses variations qui, elles, dépendent de la perméabilité du matériau ; la durée du tassement mais non sa valeur dépendent aussi de la perméabilité. Pour pouvoir traiter la relation contrainte/déformation du tassement primaire au moyen d’une formule biunivoque facilitant les calculs d’application, Terzaghi a défini une constante curieuse, l’indice de compression Cc qui lie l’indice de vides du matériau e au logarithme décimal de la contrainte effective σ’ : Cc = -Δe/Δlogσ’ et pour traiter sa relation déformation/temps, il a défini une autre constante, à peine moins étrange, le coefficient de consolidation Cv ; on les mesure au moyen d’un œdomètre dans lequel l'éprouvette frettée, saturée et drainée est soumise à un effort axial croissant puis décroissant par paliers dont les durées sont adaptées aux réponses du matériau.
L’hydraulique souterraine
La théorie de l’hydraulique souterraine est fondée sur la loi de Darcy ; elle stipule que dans un matériau perméable, la vitesse d’écoulement V (Q/S) et le gradient hydraulique i (Δh/L) sont linéairement liés par une constante empirique et composite, la perméabilité k - V = k*i - qui dépendrait seulement du matériau aquifère ; en fait c’est un paramètre qui synthétise les influences spécifiques de nombreux caractères du matériau auquel on l’attribue - granulométrie, nature et forme des grains, compacité, structure... - et du fluide qui y circule - nature, viscosité, température, composition chimique... ; elle peut entre autres varier par consolidation, colmatage, débourrage… du matériau.
La perméabilité a les dimensions [L.T−1] mais pas la nature d’une vitesse ; V n’est pas la vitesse effective d’écoulement de l’eau dans le matériau mais une abstraction commode pour remplacer dans les calculs tensoriels le rapport Q/S, quantité d’eau qui passe à travers la surface unité de matériau perpendiculaire aux lignes de courant, dans l’unité de temps.
On ne peut pas prélever d’échantillons « intacts » de matériaux peu consistants et perméables comme les sables et graves alluviaux, ou fragiles comme les roches fissurées ; la perméabilité ne peut y être mesurée qu’au moyen d’essais in situ, essais Lefranc et essais de pompage dans les premiers, essais Lugeon dans les seconds. La perméabilité des matériaux assez consistants et peu perméables comme les argiles plus ou moins sableuses, se mesure au laboratoire au moyen de perméamètres à charge variable comme un œdomètre aménagé, généralement au cours d’un essai de consolidation. Lors d’un essai, on mesure les débits stabilisés correspondant à des charges successivement augmentées ; on trace ensuite le diagramme débit/charge, une droite lissée dont la pente mesure la perméabilité.
Les méthodes de calcul
Ces théories ont été développées pour faciliter la résolution de problèmes types au moyen de méthodes graphiques et/ou analytiques relativement simples à utiliser ; on n’a pu le faire qu’en multipliant les hypothèses simplificatrices ; les méthodes les plus simples en imposent le plus et doivent donc être utilisées avec circonspection pour résoudre des problèmes pratiques.
La plupart des formules géomécaniques ont des expressions très compliquées, souvent trigonométriques ; en pratique avec du papier et un crayon, il était impossible de les utiliser sans risque d’erreur et de vérifier leurs résultats ; c’est la raison pour laquelle de nombreux abaques et tables de résultats partiels ont été établis et sont toujours utilisés, bien que maintenant, on puisse effectuer ces calculs automatiquement sans risque d’erreur – sauf de données… en vérifiant tout de même le résultat au moyen de l’abaque correspondant.
La géomécanique manipule des grandeurs qui, sous des appellations différentes, ont les mêmes dimensions - force, poids, effort, charge, poussée, butée : [M.L.T−2] - pression, contrainte, module, cohésion, résistance unitaire : [M.L−1.T−2]... Pour rendre homogènes certaines formules qui les utilisent, elle y introduit souvent des « coefficients de formes » plus ou moins mystérieux.
Le modèle élasto-plastique de Hooke/Coulomb
Les théories de l’élasticité (Hooke), de la plasticité et de la rupture (Coulomb) s’appliquent en continuité à la déformation d’un milieu monophasique soumis à un effort croissant qui, dans le modèle élasto-plastique de Hooke/Coulomb, subit successivement une déformation élastique, une déformation plastique, une rupture et un glissement.
En pratique, on sépare les études de déformation des études de rupture. En effet, atteindre l’état limite de service du géomatériau est inacceptable, car une déformation plastique de ce matériau peut entraîner de graves dommages sinon la ruine d’ouvrages mal adaptés à la subir et qui seraient ainsi au-delà de leur état limite ultime ; c’est l’application d’un coefficient de sécurité au résultat du calcul qui permet en principe que l’ensemble géomatériau-ouvrage soit en état « élastique ».
L’équilibre élastique
Boussinesq a calculé les contraintes et les déplacements dans un milieu élastique, semi-infini, sans tension initiale et donc non pesant, limité par un plan infini, soumis à un effort extérieur. Pour l’effet d’une charge ponctuelle, perpendiculaire à la surface du milieu, il a établi une formule assez compliquée, mais les géomécaniciens n’ont généralement besoin de connaître que la contrainte normale maximale Δz pour s’assurer qu’elle est inférieure aux limites d’élasticité et/ou de rupture du géomatériau et pour calculer le tassement selon la théorie de la consolidation ; on simplifie cette formule au moyen d’un coefficient d’influence I sans dimension que l’on trouve sous forme de table ou d’abaque dans les ouvrages de mécanique des sols ; plus simplement encore, on peut admettre qu’à des profondeurs croissantes, l’effet de la charge se répartit régulièrement sur des surfaces qui croissent selon un angle pyramidal plus ou moins arbitraire, sans qu’il en résulte de grandes différences pratiques.
Le procédé d’intégration graphique de Newmark établit l’influence d’une charge rectangulaire à la verticale d’un angle d’un rectangle : la valeur du coefficient d’influence I à une profondeur donnée dépend de cette profondeur et des dimensions du rectangle ; elle s’obtient par des tables et/ou des abaques ; on calcule l’influence d’une charge quelconque sur une surface quelconque par sommation des influences de rectangles ; ce procédé est bien adapté au calcul numérique.
Divers auteurs dont Fröhlich et Westergaard ont proposé des formules censées améliorer celle de Boussinesq ; elles sont encore plus compliquées sans que dans l’ensemble, leurs résultats pratiques soient meilleurs, car elles reposent sur les mêmes hypothèses simplificatrices générales et sur des hypothèses particulières supplémentaires.
L’équilibre plastique
L’étude de l’équilibre plastique d’un massif de matériau meuble est fondée sur l’application de la théorie de Coulomb pour définir la limite d’adhérence du matériau sur la surface de rupture. La détermination de la position et de la forme de la surface de rupture, celle de la distribution et de la valeur des contraintes sur cette surface sont les problèmes mathématiquement insolubles, ou du moins qui ne peuvent recevoir que des solutions particulières, fondées sur des hypothèses de calcul simplificatrices plus ou moins réalistes ; le massif est limité horizontalement par un socle et une surface libre, verticalement par un écran rigide ou un talus ; il est constitué d’un matériau homogène, isotrope et invariant ; il est soumis à l’action de la gravité et/ou d’une force extérieure ; la déformation plastique du matériau avant la rupture est négligée ; la surface de rupture est une surface réglée dont on ne connaît pas la position dans le massif ; perpendiculairement au plan, la largeur de la surface de rupture est infinie ; le massif dans lequel la rupture se produit était primitivement en équilibre ; l’inertie n’intervient pas dans le processus : la rupture est générale, instantanée ; les matériaux glissés disparaissent sans participer au nouvel équilibre du massif, maintenant limité à la surface de rupture dont la trace dans le plan de la figure est un segment de droite ou un arc de cercle.
L’écoulement de l’eau dans un milieu perméable
Dans un milieu perméable, l’écoulement de l’eau est supposé régi par la loi de Darcy dans le cadre de la théorie de l’hydraulique générale ; la résolution analytique de n’importe quel problème d’écoulement souterrain permanent est en principe possible mais rarement simple ; il en va à peine mieux en calcul numérique ; on préfère donc résoudre les problèmes débit/rabattement qui se posent souvent et qui s’y prêtent, au moyen de méthodes comme celle de Dupuit, la plus simple et la plus commode pour calculer le débit permanent d’ouvrages élémentaires d’épuisement, tranchées drainantes, puits... en fonction de pertes de charges dans des domaines et pour des conditions aux limites simples. Les dispositifs d’ouvrages complexes sont modélisés comme de grands ouvrages simples. Les problèmes d’écoulement en régime transitoire se traitent par la méthode de Theis.
Les applications
Les problèmes géomécaniques qu’un géotechnicien peut devoir résoudre sont innombrables : aucun site, aucun ouvrage, aucune situation n’est identique ni même analogue à un autre ; voici ceux que l’on rencontre le plus souvent et dont les solutions de principe sont les plus faciles à obtenir.
Stabilité des talus et des murs de soutènements
La stabilité d’un versant naturel, celle des parois d’une excavation ou d’un barrage « en terre », pose le problème de la stabilité d’un talus, d’un éventuel soutènement et d’un drainage. On peut le résoudre analytiquement par la méthode due à Rankine de la hauteur critique du talus - hauteur au-delà de laquelle un talus de pente donnée est potentiellement instable - et/ou du coin de Coulomb, ou graphiquement et numériquement par la méthode due à Fellenius améliorée par Bishop des tranches ou du coefficient de sécurité au glissement.
Les calculs analytiques qui découlaient de ces méthodes imposaient de nombreuses hypothèses simplificatrices mais demeuraient très compliqués ; l’informatique permet maintenant de tenir compte de tous les éléments du bilan des forces agissant sur le modèle, y compris des écoulements d'eau permanents ou non, des ouvrages existants ou projetés, des soutènements... Les plus perfectionnés fonctionnent à la manière des logiciels numériques aux éléments distincts, souvent en utilisant l’écran pour améliorer la solution en faisant subir au modèle de forme des déformations successives selon les conditions qu’on lui impose ; les sources d’imprécisions de données et/ou de calcul sont très nombreuses ; il est donc prudent sinon obligé de valider le logiciel utilisé dans un cas donné et de critiquer les résultats qu’il fournit auquel on applique un coefficient de sécurité que l’on minimise souvent pour des raisons d’économies de chantier ; c’est à la rigueur acceptable pour un avant-projet ou pour le très court terme, mais pas pour le long terme ou si un glissement éventuel est susceptible de mettre en péril un ouvrage voisin et/ou a fortiori, une vie humaine.
Fondations
Le choix du type de fondations d’un ouvrage - superficielles (semelles filantes, semelles isolées, radier), semi-profondes (puits), profondes ou spéciales (pieux ancrés, pieux flottants) – pose des problèmes géotechniques spécifiques de rupture de fondation et de stabilité d’ouvrage aux tassements, à la fois géologiques(nature des géomatériaux, structure du sous-sol du site…) géomécaniques (modèle de forme, paramètres des milieux…) et constructifs (implantation, architecture, structure…).
Les mouvements susceptibles d’affecter des fondations sont les tassements élastiques ou de consolidation, les gonflements, les ruptures plastiques, – basculements, poinçonnements ou glissements ; on doit s’accommoder des tassements ; on peut éviter les gonflements ; il est indispensable d’éviter les ruptures ; ces phénomènes sont évidemment étroitement liés en pratique, mais la géomécanique ne sait les traiter qu’indépendamment. En fait et contrairement à ce que l’on croit généralement, la stabilité des ouvrages aux tassements prime sur le risque de rupture de leurs fondations, car si la première est assurée, le second l’est à peu près sûrement – ce qu’il faut évidemment vérifier.
Ce que l’on appelle la contrainte ou la pression admissible d’une fondation est celle que l’on déduit de la charge ultime calculable par les moyens de la géomécanique en la minorant par un coefficient de sécurité (1/3 en général) – pour faire plus sérieux sans plus d’efficacité pratique, on parle maintenant de méthode semi-probabiliste de justification d’ouvrage selon l’eurocode 7 ; cette charge dépend des caractéristiques mécaniques du géomatériau d’assise, de la méthode de calcul, de la forme, de la surface et de la profondeur de la fondation…
Le cas des fondations superficielles est le plus courant en pratique :
À partir des essais de laboratoire, les calculs de rupture reposent sur des extensions de la théorie de Coulomb et les paramètres mesurés à la boite de Casagrande ou au triaxial : la méthode de Rankine/Prandtl permet le calcul de la charge ultime q d’une fondation superficielle en la considérant comme la somme d’un terme de profondeur et d’un terme de surface ; Terzaghi a proposé une « méthode approchée » tenant compte de la cohésion. Ceux de tassements reposent sur la théorie de Terzaghi et les paramètres mesurés à l’œdomètre appliqués à l’équilibre élastique selon la méthode de Boussinesq.
Selon la théorie de Ménard à partir de l’essai pressiométrique, le paramètre de rupture est la pression limite ; celui du tassement est le module pressiométrique.
Extraction de l’eau souterraine
On étudie l’extraction d’eau souterraine dans un massif constitué de matériau perméable aquifère pour l’exploiter par pompage dans un puits ou un forage ou pour y assécher une fouilles dont le fond est sous le niveau de la nappe.
En pratique, on pose un problème de relation débit/rabattement dans un ouvrage et une situation donnés ; les paramètres utilisés sont le gradient d’écoulement qui se mesure facilement à partir d’un réseau de piézomètres établi autour du point d’extraction et le coefficient de perméabilité du massif aquifère qui ne se mesure correctement qu’in situ, par essais Lefranc. La méthode de Dupuit est la plus simple et la plus commode pour résoudre ce problème. Le résultat est un ordre de grandeur qu’il faut préciser par un essai de pompage dans un puits d’essai.
Qualité des résultats géomécaniques
On peut retenir de tout ce qui précède que la géomécanique est un indispensable recueil de recettes dont la rigueur mathématique est purement formelle.
Les mots stabilité et équilibre de la statique décrivent l’état de sites et/ou d’ouvrages, sièges et/ou objets de déplacements évidemment dynamiques : le calcul géomécanique indique que tel talus de hauteur et pente données, constitué d’un matériau meuble de densité, teneur en eau, cohésion et angle de frottement donnés, est stable ; l’observation géologique de son site amène à en douter ; le talus demeure apparemment stable, parfois longtemps : le calcul avait raison ; un glissement se produit, souvent à la suite d’un orage : l’observation n’était pas trompeuse ; le calculateur avait oublié ou ignoré qu’entre temps, la roche s’altérerait : au moment du glissement, les valeurs de la densité, de la teneur en eau, de la cohésion et de l’angle de frottement du matériau n’étaient plus celles utilisées pour le calcul, et le modèle de comportement ne permettait pas d’intégrer la variabilité naturelle de ces constantes mathématiques par altération du matériau ; à géométrie constante, on peut estimer par itération les valeurs des paramètres correspondant à un glissement possible ; mais on ne saura pas comment et quand elles seront éventuellement atteintes. La critique géologique du résultat géomécanique est donc toujours nécessaire.
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- A. Caquot & J. Kerisel - Traité de mécanique des sols - 4e édition (1966) - Gauthier-Villars, Paris.

- R. L’Herminier - Mécanique des sols et des chaussées - (1967) – Sté de diffusion des techniques du BTP, Paris.

- F. Homand, P. Duffaut et al. - Manuel de mécanique des roches - t1, fondements (2000) - t2, applications (2005) - Presse de l’École des Mines, Paris.

- G. Schneebeli - Hydraulique souterraine - (1987) - Eyrolles, Paris.

Notes et références
- géomécanique, sur le site cnrtl.fr