Fractale de Liapounov
Une fractale de Liapounov (ou de Markus-Liapounov) se présente comme une image spectaculaire, obtenue automatiquement en utilisant la notion mathématique d'exposant de Liapounov. La courbe qui donne les valeurs de cet exposant en fonction du paramètre caractéristique d'une suite logistique présente des valeurs négatives dans les zones de stabilité et positives dans les zones de chaos.

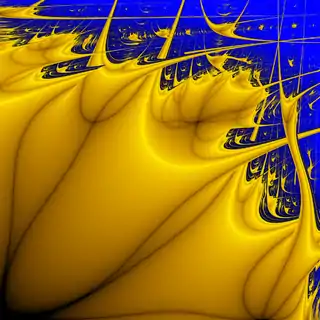

L'idée de fractale de Liapounov repose sur une suite dépendant de deux paramètres a et b. Dans le cas le plus simple une valeur obtenue à partir de la formule logistique en a est transformée par la formule en b. Il est possible d'obtenir des résultats entièrement différents en utilisant des séquences plus compliquées de a et de b. Les exposants de Liapounov correspondants sont alors présentés dans le plan (a,b).
En assignant une valeur d'intensité lumineuse distincte à chaque exposant de Liapounov négatif, claire pour l'exposant nul à la limite de la stabilité et noire pour l'exposant infini dans le cas superstable, on fait apparaître des formes donnant l'impression de relief sur un fond dans lequel les exposants positifs liés au chaos peuvent être représentés par une couleur sombre. Des agrandissements successifs font apparaître le caractère fractal d'autosimilitude[1].
Mécanisme
Considérons deux fonctions
qui caractérisent deux suites logistiques.
définit une nouvelle suite dont le comportement dépend des paramètres a et b.
À chaque paire de valeurs est associé un exposant de Liapounov qui se calcule à partir de la dérivée[2]
- .
En moyennant sur un certain nombre de pas le logarithme de la valeur de cette dérivée on obtient une approximation de l'exposant de Liapounov en tout point. Il faut souvent faire un compromis entre la précision du dessin et le temps de calcul[3].
Étude unidimensionnelle du comportement de la suite logistique
On montre que cette suite converge vers une limite stable pour des valeurs de k inférieures à 3, et diverge pour des valeurs supérieures à 4 (où la suite ne peut plus être définie pour un nombre infini d’éléments car elle dépasserait son domaine de valeur). Pour la plupart des valeurs de k entre 3,57 (environ) et 4 (bornes exclues) la suite (qui représente l’évolution d'une population dans le temps) présente un comportement chaotique, indépendant de la valeur de départ (les autres valeurs de k résultent en une suite convergeant vers un cycle constant comprenant un nombre fini de valeurs).
On montre que le critère chaotique de la suite est obtenu lorsque l’exposant de Liapounov (qui représente le logarithme moyen de croissance de la population) calculé sur la suite est positif mais inférieur à 1. Lorsque cet exposant est négatif, la population décroît et converge vers 0. Lorsque l’exposant est supérieur à 1, la population croît infiniment.
Fonction fractale unidimensionnelle
Une courbe fractale (chaotique) unidimensionnelle est alors obtenue par l'évaluation de l’exposant de Liapounov en fonction de k. L’exposant de Liapounov de la suite est facilement calculable si la fonction est dérivable sur le domaine de valeurs de la suite P, comme suit :
- , ici
Il faut noter toutefois que la somme ci-dessus n’est pas toujours convergente et tend vers moins l’infini pour des valeurs fixes de k, mais elle est continue entre ces valeurs. Ces points de discontinuité sont plus nombreux et dispersés chaotiquement dans la zone de chaos de la suite P où l’exposant prend le plus souvent des valeurs positives. Cela signifie qu’il existe une infinité d’intervalles dans cette zone où la suite P est chaotique, séparé par une infinité de très petits intervalles pour k où l’exposant de Liapounov prend des valeurs négatives et où la suite P tend vers un cycle (d’autant plus rapidement que cet exposant est fortement négatif).
Pour accélérer les calculs de l’exposant de Liapounov sur de grandes valeurs de n (et augmenter la précision du résultat), on pourra grouper les éléments de la somme par groupes de taille finie et en n'effectuant que leur produit, tant que ce produit ne dépasse pas les bornes limites de précision du résultat, et en ne sommant que les logarithmes du produit de chaque groupe. (Au sein de chaque produit il n'est pas nécessaire d'évaluer la valeur absolue de chaque terme, la valeur absolue pouvant être reportée juste avant l’évaluation du logarithme).
Obtention d’une fractale bidimensionnelle
Le comportement chaotique peut être calculé aussi simplement en appliquant successivement la fonction logistique mais en alternant cycliquement les valeurs du degré k de la croissance de la population, dans un cycle n'utilisant que deux valeurs a et b, cette périodicité se nomme racine. Par exemple, pour la séquence racine (a, b) de périodicité 2, on obtient la suite :
en fixant arbitrairement les valeurs initiales et dans le domaine de valeur ]0,1[ où la suite n’est pas constante et nulle dès les premiers éléments.
Si on ne considère que la sous-suite des éléments d’indice pair (c'est-à-dire multiples de la période du cycle de constante), elle peut s'exprimer simplement à l’aide d’une fonction unique :
- , et
et le caractère chaotique ou non de la nouvelle suite se calcule de la même façon avec l’exposant de Liapounov appliqué cette fois à la fonction caractéristique de la sous-suite (et de la suite tout entière...). Il suffit que soit dérivable, ce qui est le cas car les fonctions (ou ) sont dérivables pour toute valeur des constantes ou .
Pour dessiner la fractale, on définit un rectangle dont l’axe horizontal correspond au paramètre a et l’axe vertical au paramètre b. Pour chaque point (a, b), on calcule l’exposant de Liapounov. On attribue une couleur à ce point en fonction du résultat (et une couleur distincte dans le cas où l’évaluation de l’exposant de Liapounov ne converge pas vers une valeur finie). On obtient une figure semblable à la première image fractale ci-dessus (où les couleurs des points sur la diagonale principale correspondent au développement fractal unidimensionnel de l'exposant de Liapounov sur la suite logistique présentée précédemment).
La figure présente une relative symétrie de part et d'autre de la diagonale, mais cette symétrie n'est pas parfaite car l'ordre d'utilisation des constantes a et b dans la suite P est décalé d’une position, ce qui affecte la somme totale de l’exposant de Liapounov (approché sur un nombre nécessairement fini d’éléments), les suites différant principalement par leur premier terme considéré.
Par contre, les images obtenues diffèrent peu dans leur structure suivant la valeur définie pour le premier élément de la suite ; en pratique, on choisira souvent .
D’autres fractales similaires bi-dimensionnelles peuvent être obtenues en modifiant le motif du cycle racine, ou avec une périodicité supérieure (mais on augmente le degré du polynôme f, et donc le temps de calcul de l’image). Par exemple avec le cycle de période 5 (a, a, b, a, b) comme dans la seconde image fractale ci-dessus.
On peut également obtenir des fractales de dimension supérieure en augmentant le nombre de paramètres, par exemple avec le cycle (a, b, c), et dont on peut utiliser une projection dans un plan quelconque pour obtenir une image bidimensionnelle (par exemple en fixant c, ce qui permet une infinité d’images fractales en fonction de la valeur de c).
Ces types de fractales modélisent bien par exemple le développement d’organismes pluricellulaires ou la croissance de cristaux, soumis à des concentrations de nutriments ou des expositions thermiques ou lumineuses graduées, ou des champs de force variables en fonction de l’espace, et peuvent expliquer la formation de figures géométriques régulières et fractales.


















